3.3圆心角(2)
图片预览





文档简介
课件21张PPT。3.3圆心角(2)圆的对称性 圆的轴对称性
(圆是轴对称图形)垂径定理及其推论圆的中心对称性
(旋转不变性)圆心角定理温故知新条件结论在同圆或等圆中
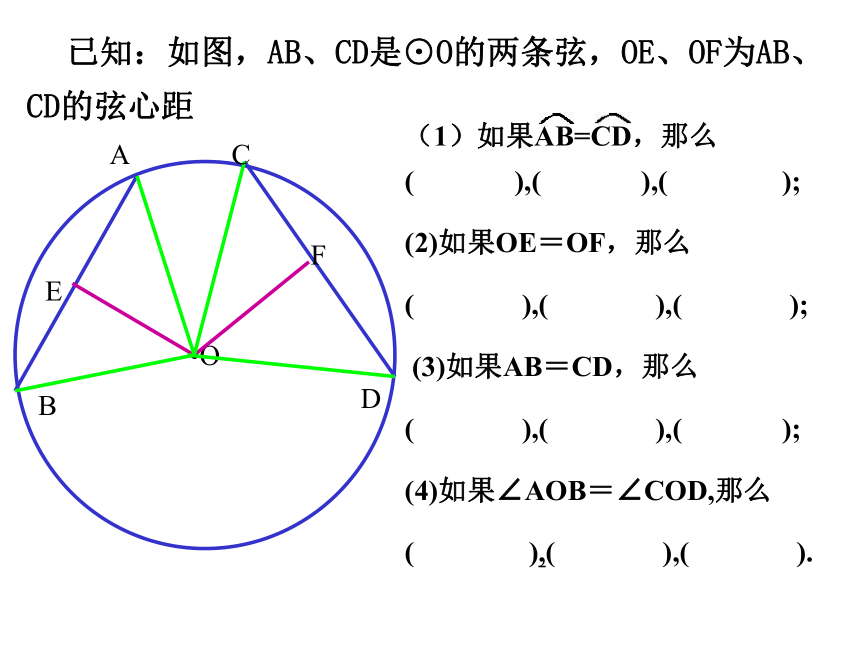
如果圆心角相等那么圆心角所对的弧相等圆心角所对的弦相等圆心角所对的弦的弦心距相等 圆心角定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。温故知新请说出定理的逆命题1.逆命题 : 在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等,所对的弦的弦心距相等。2.逆命题 : 在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧相等,弦的弦心距相等。3.逆命题 : 在同圆或等圆中,相等的弦心距对应弦相等,弦所对的圆心角相等,所对的弧相等。(1)如果AB=CD,那么( ),( ),( );
(2)如果OE=OF,那么
( ),( ),( );
(3)如果AB=CD,那么
( ),( ),( );
(4)如果∠AOB=∠COD,那么
( ),( ),( ). 已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。1、判断:
(1)等弦所对的弧相等。 ( )
(2)等弧所对的弦相等。 ( )
(3)圆心角相等,所对的弦相等。( )
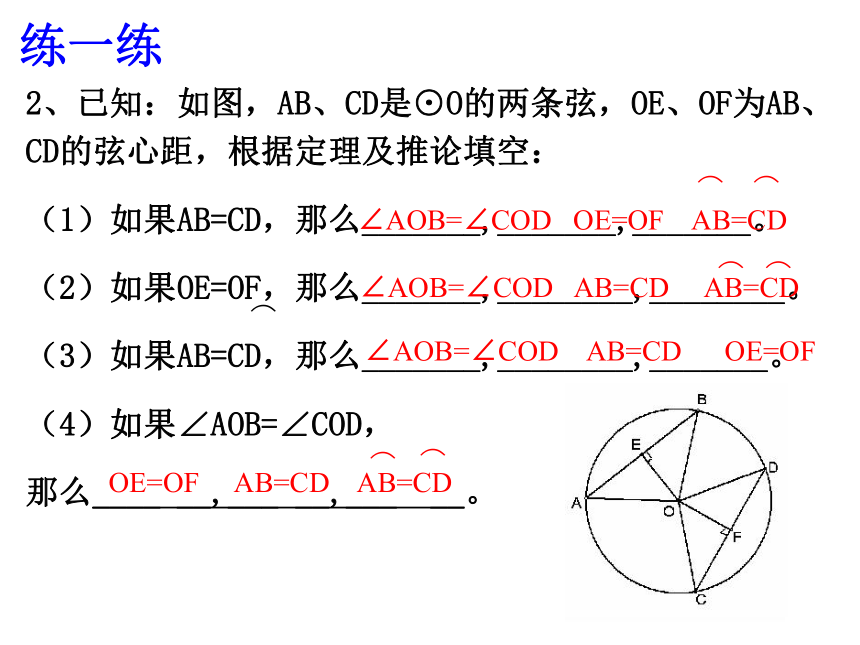
(4)弦相等,所对的圆心角相等。( ) ×××√练一练×(5)在同圆或等圆中,相等的弦所对的弧相等( )2、已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,根据定理及推论填空:
(1)如果AB=CD,那么_______,_______,_______。
(2)如果OE=OF,那么_______,________,________。
(3)如果AB=CD,那么_______,________,_______。
(4)如果∠AOB=∠COD,
那么____ __,___ __,___ __。⌒
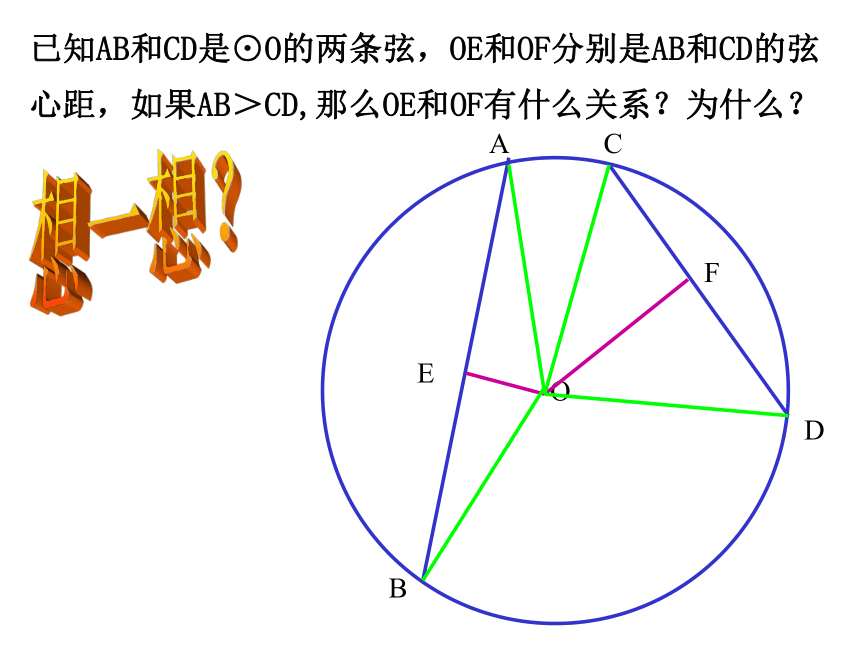
∠AOB=∠COD AB=CD OE=OF练一练?OABCDEF已知AB和CD是⊙O的两条弦,OE和OF分别是AB和CD的弦心距,如果AB>CD,那么OE和OF有什么关系?为什么?想一想?例1、如图,等边三角形ABC内接于⊙O,连结OA,OB,OC.⑴ ∠AOB 、∠COB、 ∠AOC分别为多少度?DP⑶判断四边形BDCO是哪一种特殊四边形,并说明理由。⑷若⊙O的半径为r,求等边ABC三角形的边长?⑸若等边三角形ABC的边长r,求⊙O的半径为多少? 当r = 时求圆的半径? 解(3)四边形BDCO是菱形,理由如下:∵AB=BC=CA∴∠AOB=∠BOC=∠COA=1200∴∠BOD=1800-∠AOB=600同理:∠COD=600又∵OB=OD∴OB=OD=BD同理:OC=CD∴OB=OC=BD=CD∴四边形BDCO是菱形(4)由菱形的性质,可得OP=1/2OD=1/2r∴BP=∴BC=2BP=答:等边三角形ABC的边长为做一做2、如图⊙A与⊙B是两个等圆,直线CF∥AB,分别交⊙A于点C、D,交⊙B于点E、F。求证:∠CAD=∠EBF3、 如图,已知点O是∠EPF 的平分线上一点,P点在圆外,以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D。 求证:AB=CD分析: 联想到“角平分线的性质”,作弦心距OM、ON, 证明: 作 , 垂足分别为M 、 N 。.要证AB=CD ,只需证OM=ON做一做.如图,P点在圆上,PB=PD吗?
P点在圆内,AB=CD吗?变式练习:PBEDFO(3)四边形ACBD有可能为正方形吗?若有可能,当AB、CD有何位置关系时,四边形ACBD为正方形?为什么?例2、如图, AB、CD是⊙O的两条直径。(1)顺次连结点A、C、B、D,所得的四边形是什么特殊四边形?为什么?(2)若直径为10cm,∠AOB=1200,求四边形ACBD的周长和面积。(4)如果要把直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?最大横截面面积是多少?(5)如果这根原木长15m,问锯出地木材地体积为多少立方米(树皮等损耗略去不计)?解:如图,所得的四边形是矩形,理由如下:∵AC,BD是⊙O的直径∴AO=OC=OB=OD∴四边形ABCD是平行四边形又∵AC=BD∴四边形ABCD是矩形当AC⊥BD时,四边形ABCD是正方形∵AC=BD=30cm∴AO=BO=15cm∴S正方形ABCD=15×15÷2×4=450(cm2)=4.5×10-2(m2)∴V=4.5×10-2×15=0.675(m3)1、已知:如图,在⊙O中,弦AB=CD.
求证:AD=BC 练一练2、如图M、N为AB、CD的中点,且AB=CD.
求证:∠AMN=∠CNM归纳小结这节课我们主要学习了哪些内容证明:连结OA、OB,设分别与CD、EF交于点F、G
∵A为CD中点,B为EF中点 ∴OA⊥CD,OB⊥EF
故∠AFC=∠BGE=90°①
又由OA=OB, ∴∠OAB=∠OBA ②
且AM=BN ③
∴△AFM≌△BGN(SAS) ∴AF=BG
∴OF=OG
∴DC=EF 拓展提高下课了
(圆是轴对称图形)垂径定理及其推论圆的中心对称性
(旋转不变性)圆心角定理温故知新条件结论在同圆或等圆中
如果圆心角相等那么圆心角所对的弧相等圆心角所对的弦相等圆心角所对的弦的弦心距相等 圆心角定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。温故知新请说出定理的逆命题1.逆命题 : 在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等,所对的弦的弦心距相等。2.逆命题 : 在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧相等,弦的弦心距相等。3.逆命题 : 在同圆或等圆中,相等的弦心距对应弦相等,弦所对的圆心角相等,所对的弧相等。(1)如果AB=CD,那么( ),( ),( );
(2)如果OE=OF,那么
( ),( ),( );
(3)如果AB=CD,那么
( ),( ),( );
(4)如果∠AOB=∠COD,那么
( ),( ),( ). 已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。1、判断:
(1)等弦所对的弧相等。 ( )
(2)等弧所对的弦相等。 ( )
(3)圆心角相等,所对的弦相等。( )
(4)弦相等,所对的圆心角相等。( ) ×××√练一练×(5)在同圆或等圆中,相等的弦所对的弧相等( )2、已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,根据定理及推论填空:
(1)如果AB=CD,那么_______,_______,_______。
(2)如果OE=OF,那么_______,________,________。
(3)如果AB=CD,那么_______,________,_______。
(4)如果∠AOB=∠COD,
那么____ __,___ __,___ __。⌒
∠AOB=∠COD AB=CD OE=OF练一练?OABCDEF已知AB和CD是⊙O的两条弦,OE和OF分别是AB和CD的弦心距,如果AB>CD,那么OE和OF有什么关系?为什么?想一想?例1、如图,等边三角形ABC内接于⊙O,连结OA,OB,OC.⑴ ∠AOB 、∠COB、 ∠AOC分别为多少度?DP⑶判断四边形BDCO是哪一种特殊四边形,并说明理由。⑷若⊙O的半径为r,求等边ABC三角形的边长?⑸若等边三角形ABC的边长r,求⊙O的半径为多少? 当r = 时求圆的半径? 解(3)四边形BDCO是菱形,理由如下:∵AB=BC=CA∴∠AOB=∠BOC=∠COA=1200∴∠BOD=1800-∠AOB=600同理:∠COD=600又∵OB=OD∴OB=OD=BD同理:OC=CD∴OB=OC=BD=CD∴四边形BDCO是菱形(4)由菱形的性质,可得OP=1/2OD=1/2r∴BP=∴BC=2BP=答:等边三角形ABC的边长为做一做2、如图⊙A与⊙B是两个等圆,直线CF∥AB,分别交⊙A于点C、D,交⊙B于点E、F。求证:∠CAD=∠EBF3、 如图,已知点O是∠EPF 的平分线上一点,P点在圆外,以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D。 求证:AB=CD分析: 联想到“角平分线的性质”,作弦心距OM、ON, 证明: 作 , 垂足分别为M 、 N 。.要证AB=CD ,只需证OM=ON做一做.如图,P点在圆上,PB=PD吗?
P点在圆内,AB=CD吗?变式练习:PBEDFO(3)四边形ACBD有可能为正方形吗?若有可能,当AB、CD有何位置关系时,四边形ACBD为正方形?为什么?例2、如图, AB、CD是⊙O的两条直径。(1)顺次连结点A、C、B、D,所得的四边形是什么特殊四边形?为什么?(2)若直径为10cm,∠AOB=1200,求四边形ACBD的周长和面积。(4)如果要把直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?最大横截面面积是多少?(5)如果这根原木长15m,问锯出地木材地体积为多少立方米(树皮等损耗略去不计)?解:如图,所得的四边形是矩形,理由如下:∵AC,BD是⊙O的直径∴AO=OC=OB=OD∴四边形ABCD是平行四边形又∵AC=BD∴四边形ABCD是矩形当AC⊥BD时,四边形ABCD是正方形∵AC=BD=30cm∴AO=BO=15cm∴S正方形ABCD=15×15÷2×4=450(cm2)=4.5×10-2(m2)∴V=4.5×10-2×15=0.675(m3)1、已知:如图,在⊙O中,弦AB=CD.
求证:AD=BC 练一练2、如图M、N为AB、CD的中点,且AB=CD.
求证:∠AMN=∠CNM归纳小结这节课我们主要学习了哪些内容证明:连结OA、OB,设分别与CD、EF交于点F、G
∵A为CD中点,B为EF中点 ∴OA⊥CD,OB⊥EF
故∠AFC=∠BGE=90°①
又由OA=OB, ∴∠OAB=∠OBA ②
且AM=BN ③
∴△AFM≌△BGN(SAS) ∴AF=BG
∴OF=OG
∴DC=EF 拓展提高下课了
同课章节目录
