4.1比例线段(1)

课件20张PPT。第四章 相似形三角形
4.1比例线段(一)9︰12 =6︰8 =9︰12 = 6︰83︰43︰4已知:a=-2,b=6,c=3,d=-9,
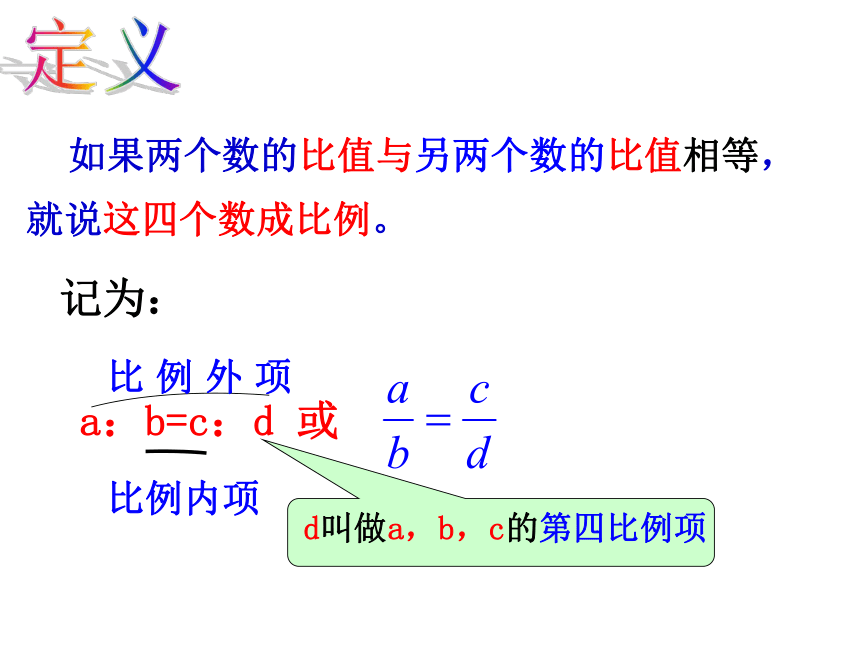
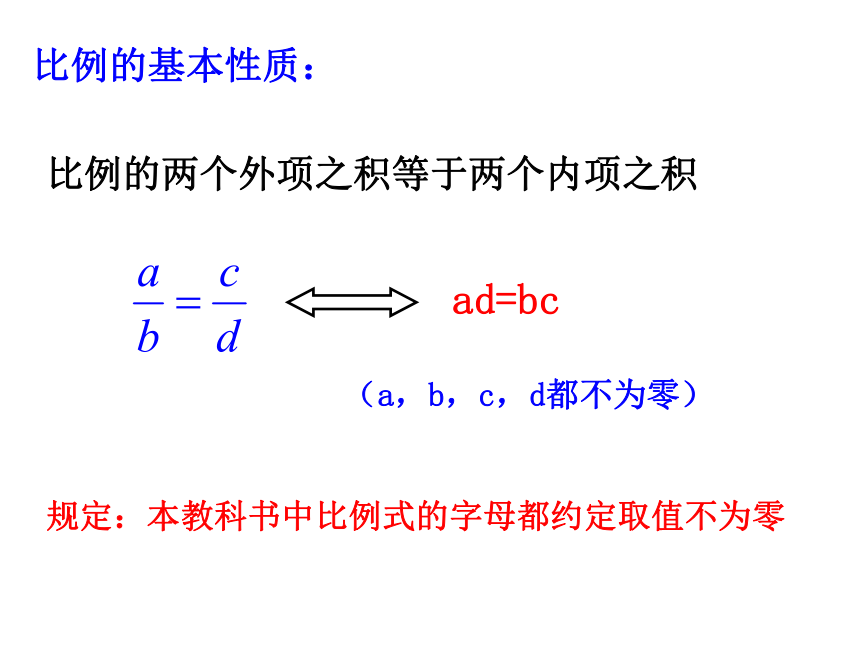
求a：b和c：d结论：a：b=c：d或 如果两个数的比值与另两个数的比值相等， 就说这四个数成比例。a：b=c：d 或比例内项比 例 外 项定义记为：1、已知:a=-2,b=4,c=-8，求a：b和b：c的值。结论：a：b=b：c： 若当两个比例内项相同时，则称b是a和c的比例中项。或做一做2、请指出下列比例式的比例内项和比例外项,并比较它们的积.做一做3、利用等式性质，能从 推导出ad=bc吗？反过来呢比例的基本性质：比例的两个外项之积等于两个内项之积ad=bc（a，b，c，d都不为零）规定：本教科书中比例式的字母都约定取值不为零 下列各组数能否成比例?如果能成比例,请写出一个比例式,并指出比例的内项与外项.试一试:例1（1）根据下列条件,求a:b的值.（2）求下列比例式中的 x.练一练已知ab=cd,请写出有关a,b,c,d成立的比例式.
(至少写4个)例2、已知 判断下列比例式是否
成立,并说明理由解（1）比例式成立，理由如下两边同加1，得：即：（2）设 =k，则a=bk，c=dk比例式变形的常用方法:k(1)已知：x：(x+1)=(1—x)：3，求x。练一练练一练1、已知 ，求 的值。2、若比例式 0，求 的值。2.已知x:y:z=4:5:7,求 ， 3.已知x：y=3：4，x：z=2：3，
求x：y：Z的值。拓展练习4、如图,已知线段AB=4,AC=2,BC=3,且
求DC,BD的长.5、如图,已知线段AD=2, AB=5, AE=1.5 ，且 ，求AC.课堂小结:比例有如下性质:比例式变形的常用方法:k探究活动 在平面直角坐标系中,过点(a,b)和原点的直线是一个怎样的正比例函数的图象?如果a,b,c,d四个数成比例,你认为点(a,b),点(c,d)和原点在同一条直线上吗?解：点（a，b），点（c，d）和坐标原点在同一条直线y＝ x上。理由：∴原点，（a，b），（c，d）在同一直线上显然(c,d)在直线y＝ x上∴直线y＝ x也可以表示为y＝ x∵a，b，c，d成比例 ∴ k＝ =则k＝∴y＝ x设经过点（a，b）和原点的直线为y＝kx再见！