沪教版四年级下册数学解决问题(2) 课件(共13张PPT)
文档属性
| 名称 | 沪教版四年级下册数学解决问题(2) 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-07 21:51:39 | ||
图片预览



文档简介
(共13张PPT)
解决问题(2) ④
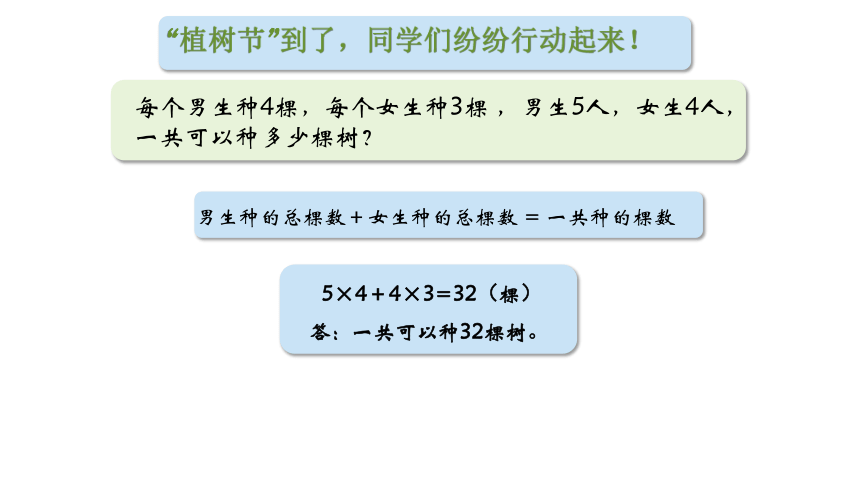
“植树节”到了,同学们纷纷行动起来!
每个男生种4棵,每个女生种3棵 ,男生5人,女生4人,一共可以种多少棵树?
5×4+4×3=32(棵)
男生种的总棵数+女生种的总棵数 = 一共种的棵数
答:一共可以种32棵树。
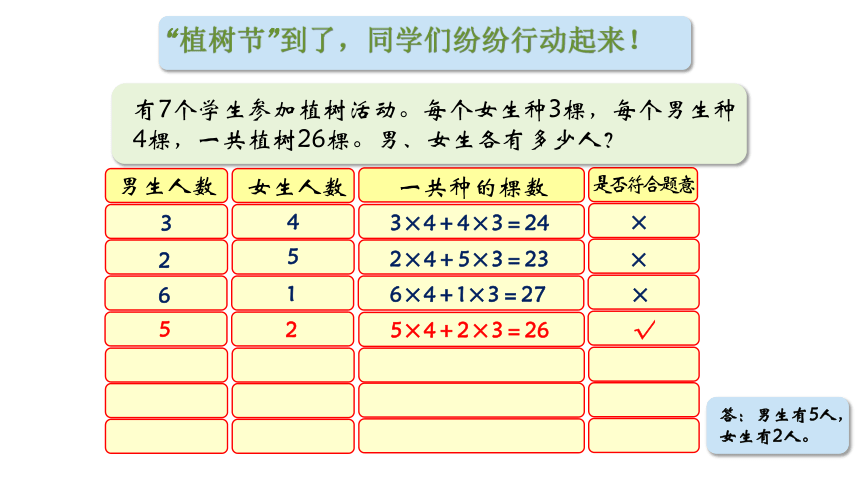
“植树节”到了,同学们纷纷行动起来!
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
每个男生种4棵,每个女生种3棵 ,男生5人,女生4人,一共可以种多少棵树?
男生5人,女生4人,
男、女生各有多少人?
一共可以种多少棵树?
一共植树26棵。
“植树节”到了,同学们纷纷行动起来!
( )×4 +( )×3
人数
人数
=26
共7人
每个男生种4棵,每个女生种3棵 ,男生5人,女生4人,一共可以种多少棵树?
男生5人,女生4人,
一共可以种多少棵树?
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
男、女生各有多少人?
一共植树26棵。
男生种的总棵数+女生种的总棵数 = 一共种的棵数
?人
?人
26棵
2×4 + 5×3
×
男生
2人
女生
5人
= 23(棵)
4
3
“植树节”到了,同学们纷纷行动起来!
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
男生人数
女生人数
一共种的棵数
3
4
3×4+4×3=24
2
5
2×4+5×3=23 ×
6
1
6×4+1×3=27 ×
5
2
5×4+2×3=26 √
答:男生有5人,女生有2人。
是否符合题意
×
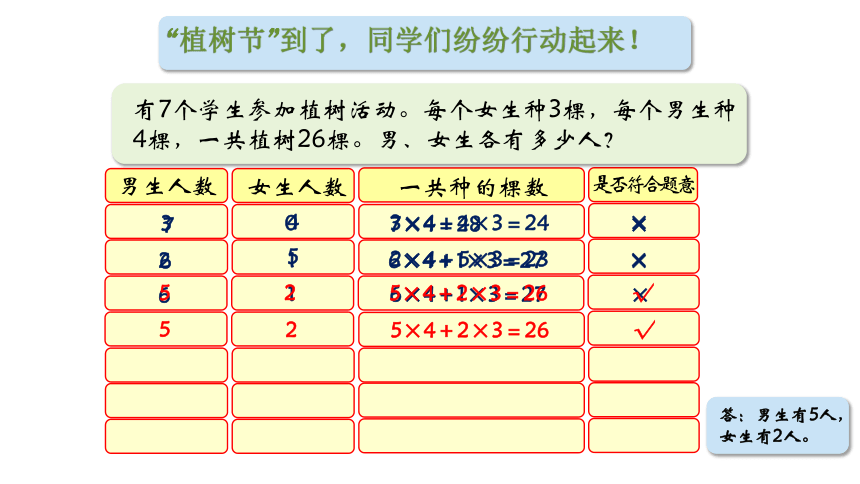
“植树节”到了,同学们纷纷行动起来!
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
男生人数
女生人数
一共种的棵数
3
4
3×4+4×3=24
2
5
2×4+5×3=23 ×
6
1
6×4+1×3=27 ×
5
2
5×4+2×3=26 √
答:男生有5人,女生有2人。
×
7
0
7×4=28 ×
6
1
6×4+1×3=27 ×
5
2
5×4+2×3=26 √
是否符合题意
5
2
5×4+2×3=26 √
6
1
6×4+1×3=27 ×
7
0
7×4=28 ×
“植树节”到了,同学们纷纷行动起来!
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
男生人数
女生人数
一共种的棵数
答:男生有5人,女生有2人。
0
7
7×3=21 ×
1
6
1×4+6×3=22 ×
2
5
2×4+5×3=23 ×
3
4
3×4+4×3=24 ×
4
3
4×4+3×3=25 ×
5
2
5×4+2×3=26 √
6
1
6×4+1×3=27 ×
是否符合题意
“植树节”到了,同学们纷纷行动起来!
男生种的总棵数+女生种的总棵数 = 一共种的棵数
答:男生有5人,女生有2人。
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
是否符合题意
是否符合题意
“植树节”到了,同学们纷纷行动起来!
有8个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
男生人数
女生人数
一共种的棵数
是否符合题意
“植树节”到了,同学们纷纷行动起来!
有8个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
假设全是女生,尝试的次数少。
怎么知道选择哪种方法更简单快速呢?
解题时要有策略。
答:男生有2人,女生有6人。
答:男生有2人,女生有6人。
相差6棵
相差2棵
是否符合题意
是否符合题意
“植树节”到了,同学们纷纷行动起来!
有13个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树43棵。男、女生各有多少人?
假设都是女生:
13×3=39(棵)
43-39=4(棵)
相差
假设都是男生:
13×4=52(棵)
52-43=9(棵)
相差
0
13
13×3=39 ×
1
12
1×4+12×3=40 ×
2
11
2×4+11×3=41 ×
3
10
3×4+10×3=42 ×
4
9
4×4+9×3=43 √
答:男生有4人,女生有9人。
男生人数
女生人数
一共种的棵数
是否符合题意
解决问题
今有雉兔同笼,
上有八头,
下有二十八足,
问雉兔各几何?
雉
一个笼子里有若干只鸡和兔,一共有8个头,
有28只脚,
问鸡和兔各有几只?
兔子的总脚数+鸡的总脚数 = 一共有的脚数
兔子的只数
鸡的只数
一共有的脚数
8
0
8×4=32 ×
7
1
7×4+1×2=30 ×
6
2
6×4+2×2=28 √
——“鸡兔同笼”问题
答:兔子有6只,鸡有2只。
一只兔有4只脚,
一只鸡有2只脚。
是否符合题意
用列表的方法来解决问题的。
在列表尝试时,还要做到有序,这样才能不重复也不遗漏。
“鸡兔同笼”问题是中国古代数学名题,出自《孙子算经》。
今天我们学习的是有关“鸡兔同笼”的问题。
解决问题(2) ④
“植树节”到了,同学们纷纷行动起来!
每个男生种4棵,每个女生种3棵 ,男生5人,女生4人,一共可以种多少棵树?
5×4+4×3=32(棵)
男生种的总棵数+女生种的总棵数 = 一共种的棵数
答:一共可以种32棵树。
“植树节”到了,同学们纷纷行动起来!
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
每个男生种4棵,每个女生种3棵 ,男生5人,女生4人,一共可以种多少棵树?
男生5人,女生4人,
男、女生各有多少人?
一共可以种多少棵树?
一共植树26棵。
“植树节”到了,同学们纷纷行动起来!
( )×4 +( )×3
人数
人数
=26
共7人
每个男生种4棵,每个女生种3棵 ,男生5人,女生4人,一共可以种多少棵树?
男生5人,女生4人,
一共可以种多少棵树?
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
男、女生各有多少人?
一共植树26棵。
男生种的总棵数+女生种的总棵数 = 一共种的棵数
?人
?人
26棵
2×4 + 5×3
×
男生
2人
女生
5人
= 23(棵)
4
3
“植树节”到了,同学们纷纷行动起来!
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
男生人数
女生人数
一共种的棵数
3
4
3×4+4×3=24
2
5
2×4+5×3=23 ×
6
1
6×4+1×3=27 ×
5
2
5×4+2×3=26 √
答:男生有5人,女生有2人。
是否符合题意
×
“植树节”到了,同学们纷纷行动起来!
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
男生人数
女生人数
一共种的棵数
3
4
3×4+4×3=24
2
5
2×4+5×3=23 ×
6
1
6×4+1×3=27 ×
5
2
5×4+2×3=26 √
答:男生有5人,女生有2人。
×
7
0
7×4=28 ×
6
1
6×4+1×3=27 ×
5
2
5×4+2×3=26 √
是否符合题意
5
2
5×4+2×3=26 √
6
1
6×4+1×3=27 ×
7
0
7×4=28 ×
“植树节”到了,同学们纷纷行动起来!
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
男生人数
女生人数
一共种的棵数
答:男生有5人,女生有2人。
0
7
7×3=21 ×
1
6
1×4+6×3=22 ×
2
5
2×4+5×3=23 ×
3
4
3×4+4×3=24 ×
4
3
4×4+3×3=25 ×
5
2
5×4+2×3=26 √
6
1
6×4+1×3=27 ×
是否符合题意
“植树节”到了,同学们纷纷行动起来!
男生种的总棵数+女生种的总棵数 = 一共种的棵数
答:男生有5人,女生有2人。
有7个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
是否符合题意
是否符合题意
“植树节”到了,同学们纷纷行动起来!
有8个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
男生人数
女生人数
一共种的棵数
是否符合题意
“植树节”到了,同学们纷纷行动起来!
有8个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树26棵。男、女生各有多少人?
假设全是女生,尝试的次数少。
怎么知道选择哪种方法更简单快速呢?
解题时要有策略。
答:男生有2人,女生有6人。
答:男生有2人,女生有6人。
相差6棵
相差2棵
是否符合题意
是否符合题意
“植树节”到了,同学们纷纷行动起来!
有13个学生参加植树活动。每个女生种3棵,每个男生种4棵,一共植树43棵。男、女生各有多少人?
假设都是女生:
13×3=39(棵)
43-39=4(棵)
相差
假设都是男生:
13×4=52(棵)
52-43=9(棵)
相差
0
13
13×3=39 ×
1
12
1×4+12×3=40 ×
2
11
2×4+11×3=41 ×
3
10
3×4+10×3=42 ×
4
9
4×4+9×3=43 √
答:男生有4人,女生有9人。
男生人数
女生人数
一共种的棵数
是否符合题意
解决问题
今有雉兔同笼,
上有八头,
下有二十八足,
问雉兔各几何?
雉
一个笼子里有若干只鸡和兔,一共有8个头,
有28只脚,
问鸡和兔各有几只?
兔子的总脚数+鸡的总脚数 = 一共有的脚数
兔子的只数
鸡的只数
一共有的脚数
8
0
8×4=32 ×
7
1
7×4+1×2=30 ×
6
2
6×4+2×2=28 √
——“鸡兔同笼”问题
答:兔子有6只,鸡有2只。
一只兔有4只脚,
一只鸡有2只脚。
是否符合题意
用列表的方法来解决问题的。
在列表尝试时,还要做到有序,这样才能不重复也不遗漏。
“鸡兔同笼”问题是中国古代数学名题,出自《孙子算经》。
今天我们学习的是有关“鸡兔同笼”的问题。
