1.4 二次函数的应用 同步练习 浙教版数学九年级上册(无答案)
文档属性
| 名称 | 1.4 二次函数的应用 同步练习 浙教版数学九年级上册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 335.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-08 21:25:43 | ||
图片预览



文档简介
浙教版九年级上册1.4 二次函数的应用
一、选择题
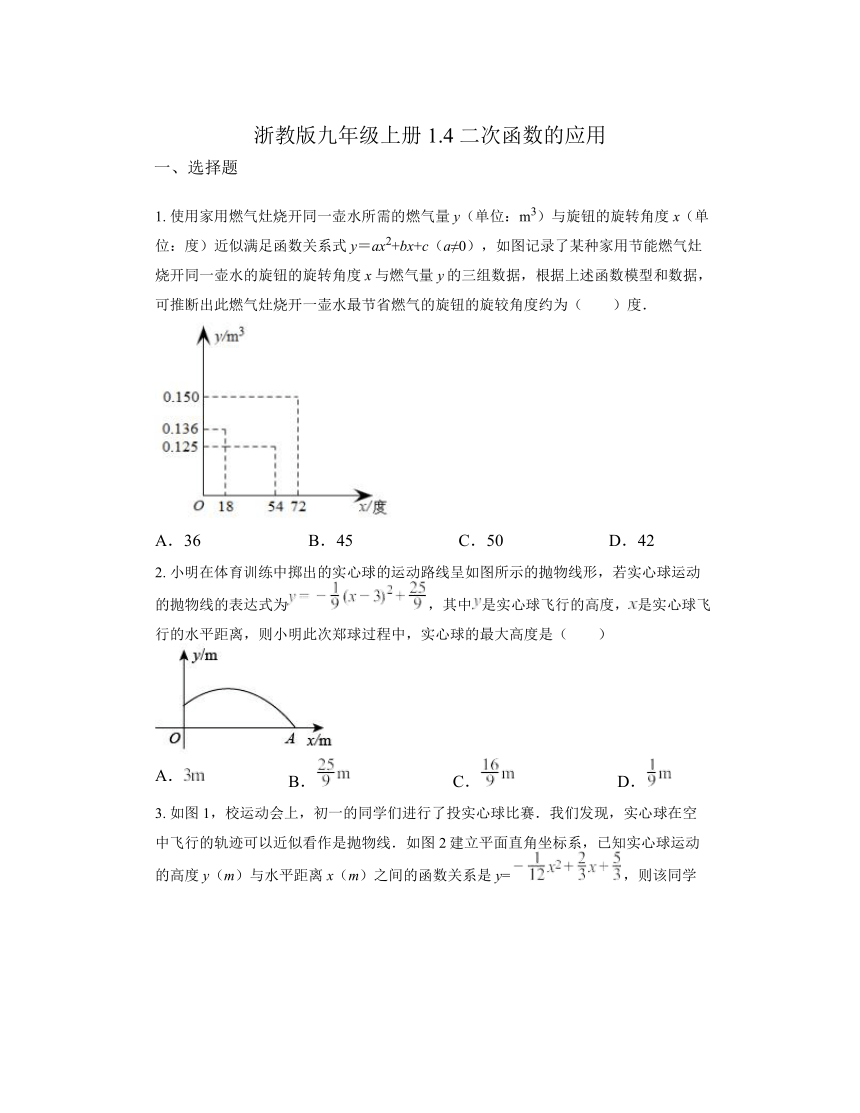
1. 使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)近似满足函数关系式y=ax2+bx+c(a≠0),如图记录了某种家用节能燃气灶烧开同一壶水的旋钮的旋转角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮的旋较角度约为( )度.
A.36 B.45 C.50 D.42
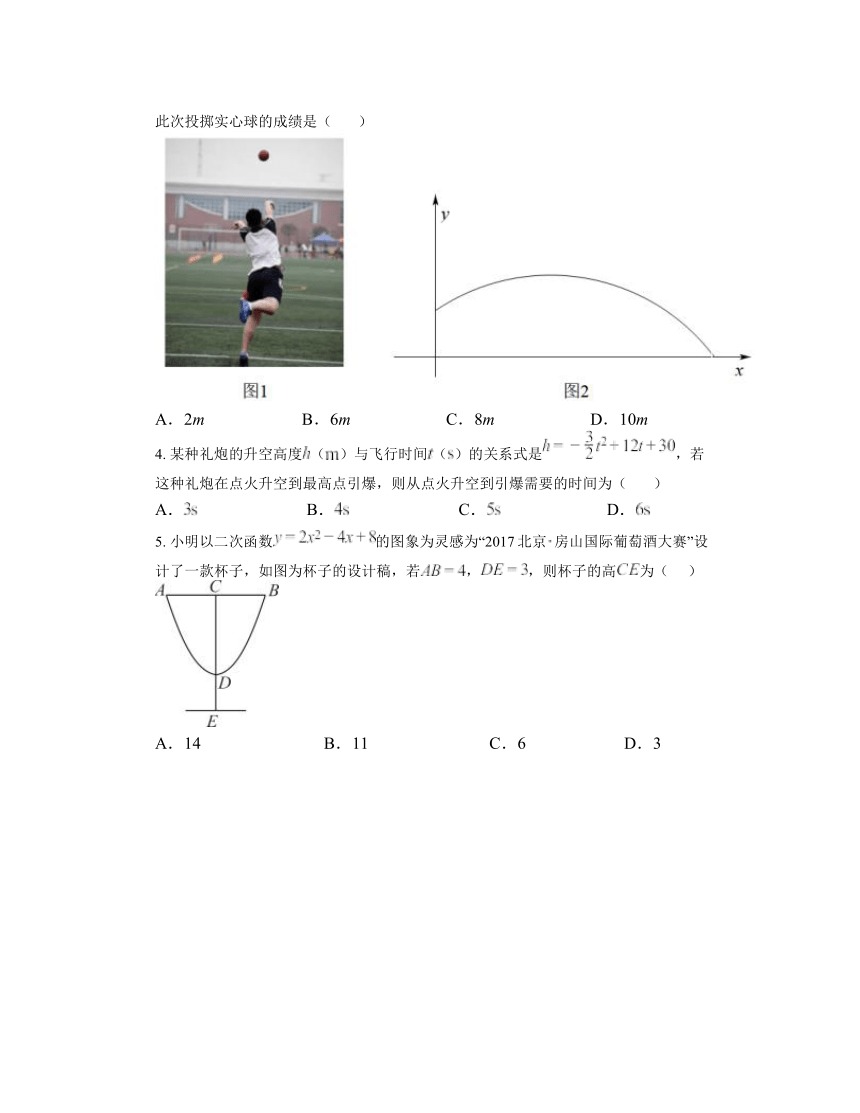
2. 小明在体育训练中掷出的实心球的运动路线呈如图所示的抛物线形,若实心球运动的抛物线的表达式为,其中是实心球飞行的高度,是实心球飞行的水平距离,则小明此次郑球过程中,实心球的最大高度是( )
A. B. C. D.
3. 如图1,校运动会上,初一的同学们进行了投实心球比赛.我们发现,实心球在空中飞行的轨迹可以近似看作是抛物线.如图2建立平面直角坐标系,已知实心球运动的高度y(m)与水平距离x(m)之间的函数关系是y=,则该同学此次投掷实心球的成绩是( )
A.2m B.6m C.8m D.10m
4. 某种礼炮的升空高度()与飞行时间()的关系式是,若这种礼炮在点火升空到最高点引爆,则从点火升空到引爆需要的时间为( )
A. B. C. D.
5. 小明以二次函数的图象为灵感为“2017北京房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高为( )
A.14 B.11 C.6 D.3
6. 如图,在平面直角坐标系中,抛物线y=﹣x2+2x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+AP的最小值为( ).
A. B. C.3 D.2
7. 如图,抛物线经过点,点从点A出发,沿抛物线运动到顶点后,再沿对称轴l向下运动,给出下列说法:
①:
②抛物线的对称轴为;
③当点P,B,C构成的三角形的周长取最小值时,;
④在点P从点A运动到顶点的过程中,当时,的面积最大.
其中,所有正确的说法是( )
A.①②③ B.①②④ C.②③④ D.①③
8. 如图所示,已知正方形的边长为1,分别是边的点(不与重合),且,设四边形的面积为y,,则y关于x的函数的图像大致是( )
A. B. C. D.
9. 如图,在中,,,三个全等的正方形的对称中心分别是的顶点,且它们各边与的两直角边平行或垂直.若正方形的边长为,且,阴影部分的面积为,则能反映与之间函数关系的大致图象是( )
A. B.
C. D.
10. 如图,直线,都与直线垂直,垂足分别为,,,正方形的边长为,对角线在直线上,且点位于点处,将正方形沿向右平移,直到点与点重合为止.记点平移的距离为,正方形位于直线,之间部分(阴影部分)的面积为,则关于的函数图象大致为( )
A. B.
C. D.
二、填空题
11. 飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=120t﹣2.5t2.在飞机从开始滑行到最后停止一共滑行的距离是____m.
12. 用总长为80米的篱笆围成一个面积为S平方米的矩形场地,设矩形场地的一边长为x米,则当x=______米时,矩形场地的面积S最大.
13. 如图,以的速度将小球沿与地面成角的方向击出时,小球的飞行路线将是一条抛物线.如果 不考虑空气阻力,小球的飞行高度单位:)与飞行时间单位:)之间具有函数关系.则小球从飞出到落地要用时_______________________.
14. 抛物线与直线的两个交点的横坐标分别是,,记,则代数式的值为_____.
三、解答题
15. 某商品的进价为每件40元,售价为每件60元,平均每天可卖出80件.如果每件商品的售价每下降1元,则每天可多卖出10件.设每件商品的售价下降元(为正整数),每天的销售利润为元.
(1)求销售利润(元)与下降价格(元)的函数关系式;
(2)每件商品的售价下降多少元时,每天的销售利润最大?最大利润是多少元?
16. 已知二次函数的图象经过坐标原点,与轴交于点.
(1)求二次函数的解析式;
(2)若在抛物线上存在点,满足,求点的坐标.
17. 攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市,某水果店购进一批优质晚熟芒果,进价为元千克,售价不低于元千克,且不超过元每千克,根据销售情况,发现该芒果在一天内的销售量y(千克)与该天的售价(元/千克)之间的数量满足如表所示的一次函数关系.
销售量y(千克)
售价x(元/千克)
(1)求芒果一天的销售量与该天售价之间的一次函数关系式,写出的取值范围.
(2)设某天销售这种芒果获利元,写出与售价之间的函数关系式.如果水果店该天获利元,那么这天芒果的售价为多少元?
(3)当芒果的售价为多少时,才能使销售利润最大?最大利润为多少元?
18. 如图,抛物线与x轴相交于点A、点B,与y轴相交于点C.
(1)请直接写出点A,B,C的坐标;
(2)点在抛物线上,当m取何值时,的面积最大?并求出面积的最大值.
(3)点是抛物线上的动点,作交x轴于点E,是否存在点F,使得以A、C、E、F为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F的坐标;若不存在,请说明理由.
19. 如图,抛物线,平移抛物线,使其顶点D在抛物线位于y轴右侧的图象上,得到抛物线,抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.
(1)当时,求抛物线的解析式.
(2)在抛物线的的对称轴上是否存在一点P,使得的长最短?若存在、求出点P的坐标(用含a的代数式表示);若不存在;请说明理由.
一、选择题
1. 使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)近似满足函数关系式y=ax2+bx+c(a≠0),如图记录了某种家用节能燃气灶烧开同一壶水的旋钮的旋转角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮的旋较角度约为( )度.
A.36 B.45 C.50 D.42
2. 小明在体育训练中掷出的实心球的运动路线呈如图所示的抛物线形,若实心球运动的抛物线的表达式为,其中是实心球飞行的高度,是实心球飞行的水平距离,则小明此次郑球过程中,实心球的最大高度是( )
A. B. C. D.
3. 如图1,校运动会上,初一的同学们进行了投实心球比赛.我们发现,实心球在空中飞行的轨迹可以近似看作是抛物线.如图2建立平面直角坐标系,已知实心球运动的高度y(m)与水平距离x(m)之间的函数关系是y=,则该同学此次投掷实心球的成绩是( )
A.2m B.6m C.8m D.10m
4. 某种礼炮的升空高度()与飞行时间()的关系式是,若这种礼炮在点火升空到最高点引爆,则从点火升空到引爆需要的时间为( )
A. B. C. D.
5. 小明以二次函数的图象为灵感为“2017北京房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若,,则杯子的高为( )
A.14 B.11 C.6 D.3
6. 如图,在平面直角坐标系中,抛物线y=﹣x2+2x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+AP的最小值为( ).
A. B. C.3 D.2
7. 如图,抛物线经过点,点从点A出发,沿抛物线运动到顶点后,再沿对称轴l向下运动,给出下列说法:
①:
②抛物线的对称轴为;
③当点P,B,C构成的三角形的周长取最小值时,;
④在点P从点A运动到顶点的过程中,当时,的面积最大.
其中,所有正确的说法是( )
A.①②③ B.①②④ C.②③④ D.①③
8. 如图所示,已知正方形的边长为1,分别是边的点(不与重合),且,设四边形的面积为y,,则y关于x的函数的图像大致是( )
A. B. C. D.
9. 如图,在中,,,三个全等的正方形的对称中心分别是的顶点,且它们各边与的两直角边平行或垂直.若正方形的边长为,且,阴影部分的面积为,则能反映与之间函数关系的大致图象是( )
A. B.
C. D.
10. 如图,直线,都与直线垂直,垂足分别为,,,正方形的边长为,对角线在直线上,且点位于点处,将正方形沿向右平移,直到点与点重合为止.记点平移的距离为,正方形位于直线,之间部分(阴影部分)的面积为,则关于的函数图象大致为( )
A. B.
C. D.
二、填空题
11. 飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=120t﹣2.5t2.在飞机从开始滑行到最后停止一共滑行的距离是____m.
12. 用总长为80米的篱笆围成一个面积为S平方米的矩形场地,设矩形场地的一边长为x米,则当x=______米时,矩形场地的面积S最大.
13. 如图,以的速度将小球沿与地面成角的方向击出时,小球的飞行路线将是一条抛物线.如果 不考虑空气阻力,小球的飞行高度单位:)与飞行时间单位:)之间具有函数关系.则小球从飞出到落地要用时_______________________.
14. 抛物线与直线的两个交点的横坐标分别是,,记,则代数式的值为_____.
三、解答题
15. 某商品的进价为每件40元,售价为每件60元,平均每天可卖出80件.如果每件商品的售价每下降1元,则每天可多卖出10件.设每件商品的售价下降元(为正整数),每天的销售利润为元.
(1)求销售利润(元)与下降价格(元)的函数关系式;
(2)每件商品的售价下降多少元时,每天的销售利润最大?最大利润是多少元?
16. 已知二次函数的图象经过坐标原点,与轴交于点.
(1)求二次函数的解析式;
(2)若在抛物线上存在点,满足,求点的坐标.
17. 攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市,某水果店购进一批优质晚熟芒果,进价为元千克,售价不低于元千克,且不超过元每千克,根据销售情况,发现该芒果在一天内的销售量y(千克)与该天的售价(元/千克)之间的数量满足如表所示的一次函数关系.
销售量y(千克)
售价x(元/千克)
(1)求芒果一天的销售量与该天售价之间的一次函数关系式,写出的取值范围.
(2)设某天销售这种芒果获利元,写出与售价之间的函数关系式.如果水果店该天获利元,那么这天芒果的售价为多少元?
(3)当芒果的售价为多少时,才能使销售利润最大?最大利润为多少元?
18. 如图,抛物线与x轴相交于点A、点B,与y轴相交于点C.
(1)请直接写出点A,B,C的坐标;
(2)点在抛物线上,当m取何值时,的面积最大?并求出面积的最大值.
(3)点是抛物线上的动点,作交x轴于点E,是否存在点F,使得以A、C、E、F为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F的坐标;若不存在,请说明理由.
19. 如图,抛物线,平移抛物线,使其顶点D在抛物线位于y轴右侧的图象上,得到抛物线,抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.
(1)当时,求抛物线的解析式.
(2)在抛物线的的对称轴上是否存在一点P,使得的长最短?若存在、求出点P的坐标(用含a的代数式表示);若不存在;请说明理由.
同课章节目录
