1.2 二次函数的图象 同步练习(含解析) 浙教版数学九年级上册
文档属性
| 名称 | 1.2 二次函数的图象 同步练习(含解析) 浙教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 168.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-09 10:14:38 | ||
图片预览


文档简介
浙教版九上 1.2 二次函数的图象
一、单选题(共11小题)
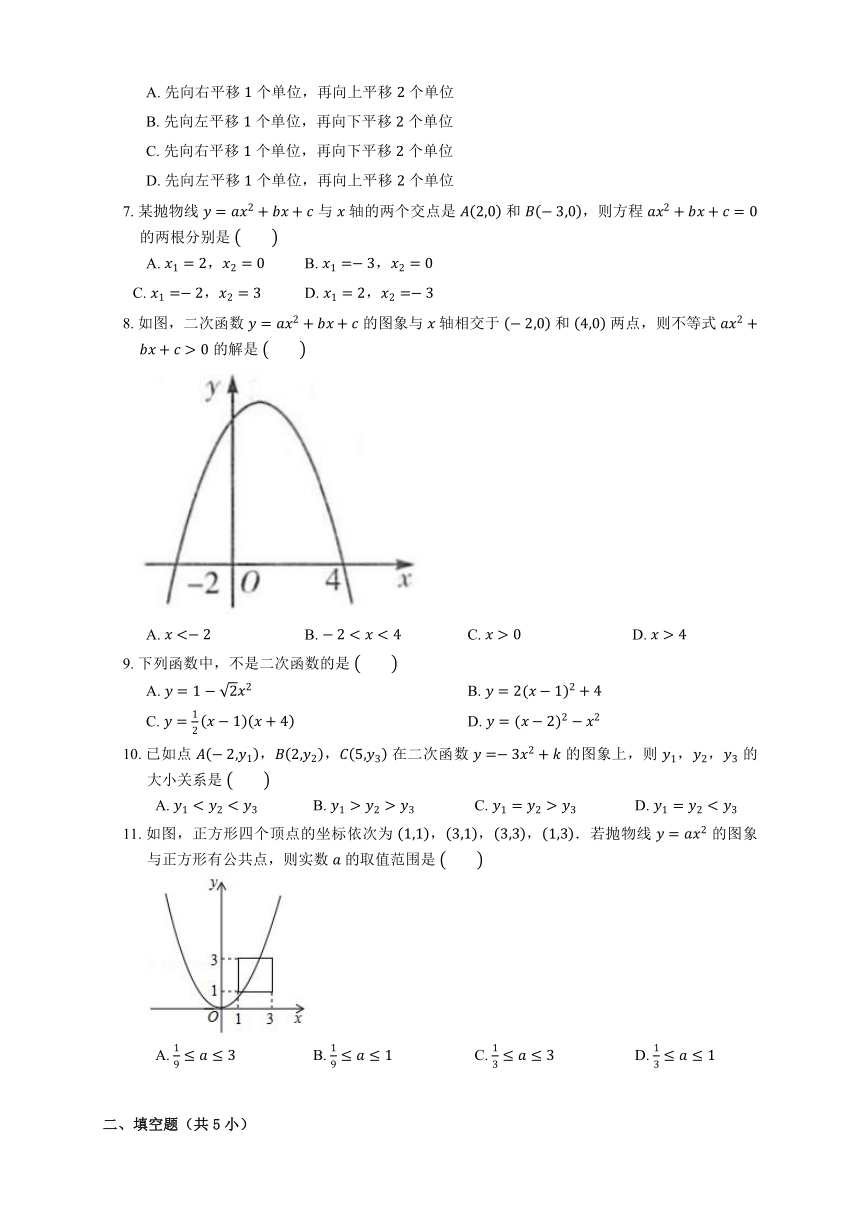
1. 如图,在 平行四边形 中,对角线 , 相交于点 ,,,.若 过点 且与边 , 分别相交于点 ,,设 ,,则 关于 的函数图象大致为
A. B.
C. D.
2. 若点 在函数 的图象上,则 的值为
A. B. C. D.
3. 设 平行于 轴,与直线 交于点 ,当 最大时, 的值为
A. B. C. D.
4. 若二次函数 的图象的最高点是 ,则 , 的值分别是
A. , B. ,
C. , D. ,
5. 二次函数 在 范围内的最大值是
A. B. C. D.
6. 抛物线 通过变换可以得到抛物线 ,以下变换过程正确的是
A. 先向右平移 个单位,再向上平移 个单位
B. 先向左平移 个单位,再向下平移 个单位
C. 先向右平移 个单位,再向下平移 个单位
D. 先向左平移 个单位,再向上平移 个单位
7. 某抛物线 与 轴的两个交点是 和 ,则方程 的两根分别是
A. , B. ,
C. , D. ,
8. 如图,二次函数 的图象与 轴相交于 和 两点,则不等式 的解是
A. B. C. D.
9. 下列函数中,不是二次函数的是
A. B.
C. D.
10. 已如点 ,, 在二次函数 的图象上,则 ,, 的大小关系是
A. B. C. D.
11. 如图,正方形四个顶点的坐标依次为 ,,,.若抛物线 的图象与正方形有公共点,则实数 的取值范围是
A. B. C. D.
二、填空题(共5小)
12. 若点 , 是二次函数 图象上的两点,那么 与 的大小关系是 .(填 , 或 )
13. 如果抛物线 与 轴交于点 ,那么点 关于此抛物线对称轴的对称点坐标是 .
14. 二次函数 的图象的对称轴是 ,在对称轴的左侧,抛物线从左到右 ;在对称轴的右侧,抛物线从左到右 .
15. 抛物线和 形状相同,方向相反,且顶点为 ,则它的关系式为 .
16. 将二次函数 先向左平移 个单位长度,再向上平移 个单位长度,得到二次函数 的图象,则 , , .
三、解答题(共5小题)
17. 在同一平面直角坐标系中,画出下面函数的图象,并尽可能多地指出两个图象间的共同点、不同点.
();
().
18. 用配方法把二次函数 化为 的形式,并指出这个函数图象的开口方向、对称轴和顶点坐标.
19. 定义:函数图象上到两坐标轴的距离都不大于 的点叫做这个函数图象的“ 阶方点”.例如,点 是函数 图象的“ 阶方点”;点 是函数 图象的“ 阶方点”.
(1)在① ;② ;③ 三点中,是反比例函数 图象的“ 阶方点”的有 (填序号);
(2)若 关于 的一次函数 图象的“ 阶方点”有且只有一个,求 的值;
(3)若 关于 的二次函数 图象的“ 阶方点”一定存在,请直接写出 的取值范围.
20. 已知抛物线 经过 ,, 三点,对称轴是直线 .关于 的方程 有两个相等的实数根.
(1)求抛物线的解析式;
(2)若 ,试比较 与 的大小;
(3)若 , 两点在直线 的两侧,且 ,求 的取值范围.
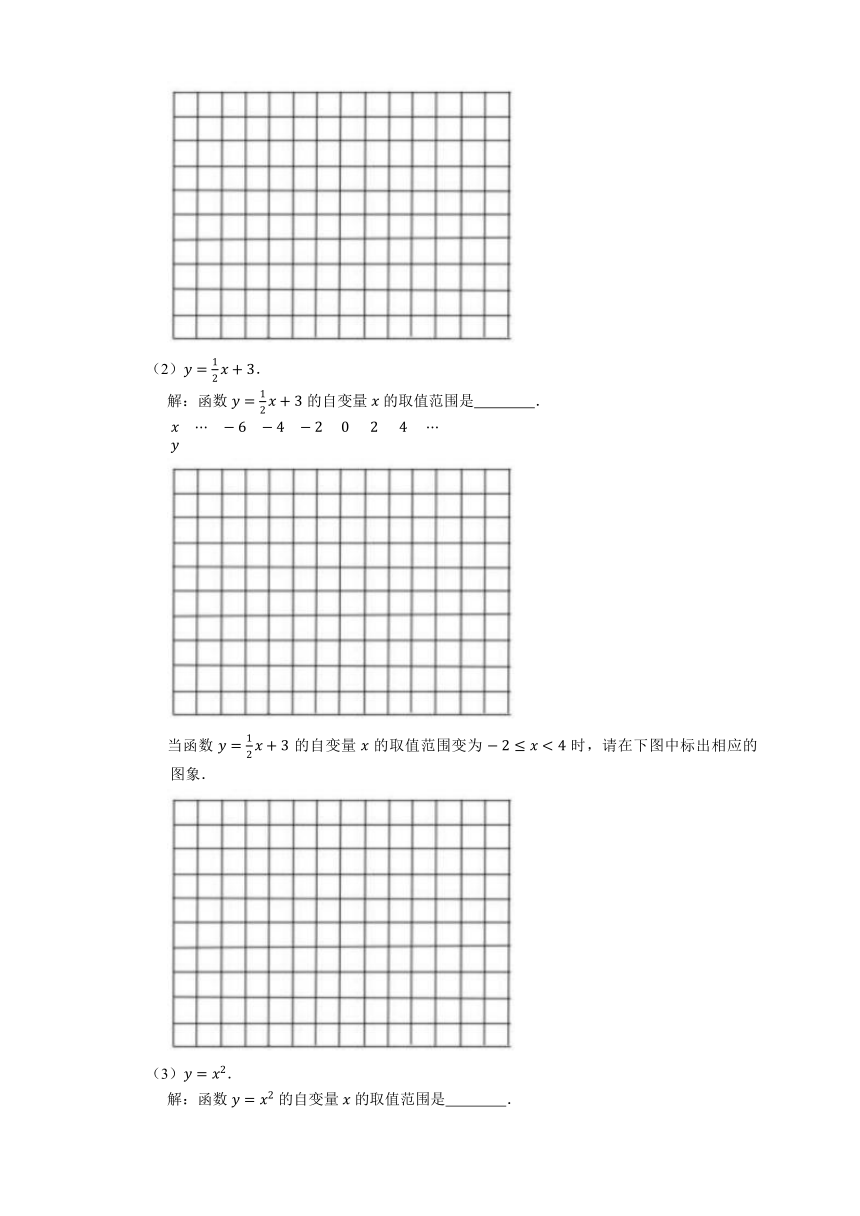
21. 用“描点法”分别画出下列各函数的图象.
(1).
解:函数 的自变量 的取值范围是 .
(2).
解:函数 的自变量 的取值范围是 .
当函数 的自变量 的取值范围变为 时,请在下图中标出相应的图象.
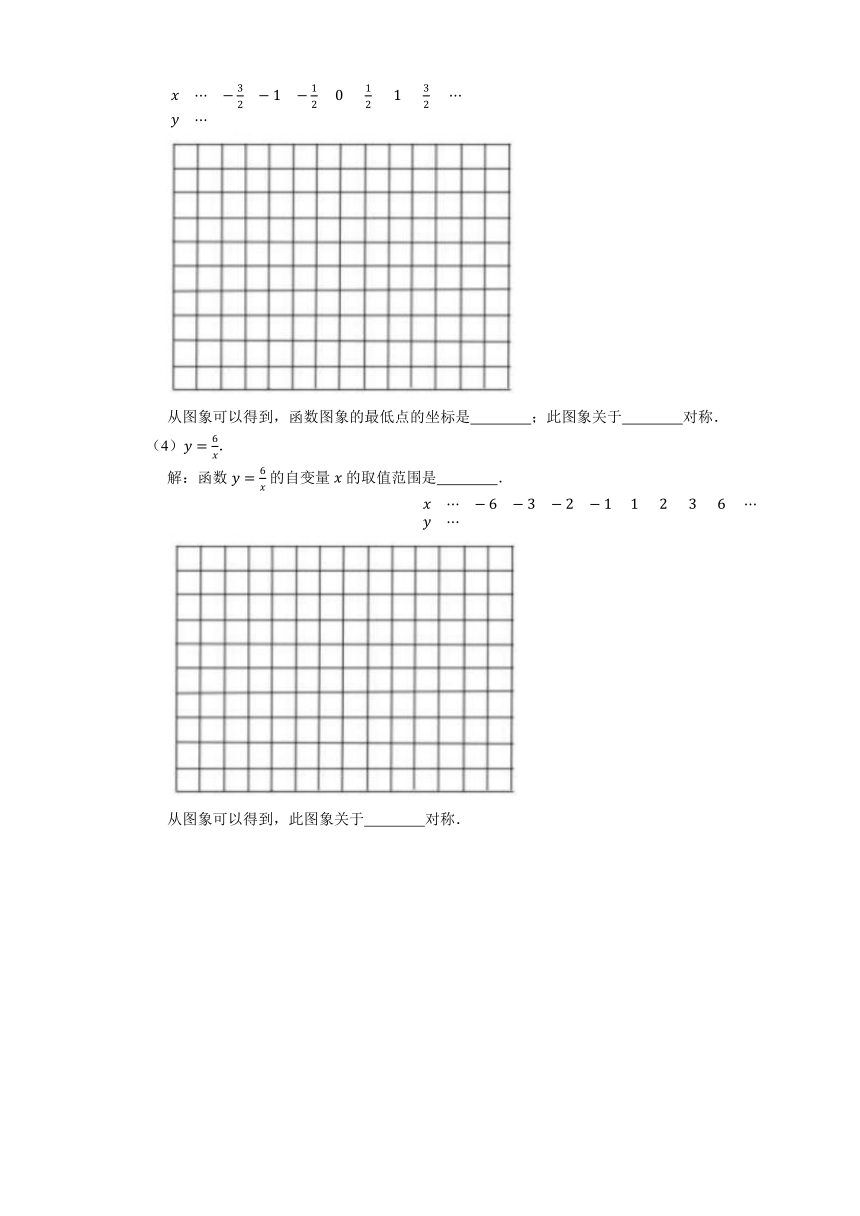
(3).
解:函数 的自变量 的取值范围是 .
从图象可以得到,函数图象的最低点的坐标是 ;此图象关于 对称.
(4).
解:函数 的自变量 的取值范围是 .
从图象可以得到,此图象关于 对称.
答案
一 单选题
1. C
【解析】过 点作 于 ,
,,
,
,
,,
四边形 为平行四边形,
,
,
,
设 ,,则 ,
,
,
,当 时 ,
故符合解析式的图象为:
故选:C.
2. C
3. B
【解析】直线的解析式为 ,
设 平行于 轴,与一次函数图象交于点
则 ,,
,
,
当 时, 最大为 .
故选:B.
4. B
5. D
【解析】,
对称轴为直线 ,
在 的取值范围内,当 时,有最大值 ,
故选:D.
6. D
7. D
【解析】抛物线与 轴的交点坐标的横坐标即为 的两根,
两个交点是 和 ,
两根分别是 ,.
故选:D.
8. B
9. D
10. C
11. A
【解析】设抛物线的解析式为 ,
当抛物线经过 时,,
当抛物线经过 时,,
观察图象可知 .
故选:A.
二 填空题
12.
13.
【解析】 抛物线 与 轴交于点 坐标为 ,对称轴为 ,
,
点 与此抛物线对称轴的对称点坐标是 .
14. ,上升,下降
15.
【解析】 抛物线的顶点坐标 ,开口方向与抛物线 的方向相反,
这个二次函数的解析式为 .
16. ,,
【解析】将二次函数 先向左平移 个单位长度,再向上平移 个单位长度,
得到二次函数 的图象,即 ,
,,.
,,.
故答案是:;;.
三 解答题
17. 略
18. ,
,
.
开口方向:向上.
顶点坐标:.
对称轴:直线 .
19. (1) ②③
【解析】① 到两坐标轴的距离分别是 ,,
所以 不是反比例函数 图象的“ 阶方点”;
② 到两坐标轴的距离分别是 ,,
所以 是反比例函数 图象的“ 阶方点”;
③ 到两坐标轴的距离分别是 ,,
所以 是反比例函数 图象的“ 阶方点”;
故答案为:②③.
(2) 因为 ,
所以函数经过定点 ,
在以 为中心,边长为 的正方形 中,当直线与正方形区域只有唯一交点时,图象的“ 阶方点”有且只有一个,
由图可知,,,
因为一次函数 图象的“ 阶方点”有且只有一个,
当直线经过点 时,,此时图象的“ 阶方点”有且只有一个,
当直线经过点 时,,此时图象的“ 阶方点”有且只有一个,
综上所述: 的值为 或 ;
(3)
【解析】在以 为中心,边长为 的正方形 中,当抛物线与正方形区域有公共部分时,二次函数 图象的“ 阶方点”一定存在,
如图,
当 时,,,,,
当抛物线经过点 时,(舍)或 ,
当抛物线经过点 时,;
所以 时,二次函数 图象有“ 阶方点”;
综上所述: 时,二次函数 图象有“ 阶方点”一定存在.
20. (1) 抛物线 经过 ,
对称轴是直线 ,
关于 的方程 有两个相等的实数根,
由 可得:
抛物线的解析式为 .
(2) ,
,,
点 ,点 在对称轴直线 的左侧,
抛物线 ,
,即 随 的增大而增大,
,
,
.
(3) 若点 在对称轴直线 的左侧,点 在对称轴直线 的右侧时,
由题意可得
,
若点 在对称轴直线 的左侧,点 在对称轴直线 的右侧时,
由题意可得:
不等式组无解,
综上所述:.
21. (1) 为全体实数,表略,图象略.
(2) 为全体实数,表略,图象略.
(3) 为全体实数,表略,图象略.
; 轴
(4) ,表略,图象略,
原点
一、单选题(共11小题)
1. 如图,在 平行四边形 中,对角线 , 相交于点 ,,,.若 过点 且与边 , 分别相交于点 ,,设 ,,则 关于 的函数图象大致为
A. B.
C. D.
2. 若点 在函数 的图象上,则 的值为
A. B. C. D.
3. 设 平行于 轴,与直线 交于点 ,当 最大时, 的值为
A. B. C. D.
4. 若二次函数 的图象的最高点是 ,则 , 的值分别是
A. , B. ,
C. , D. ,
5. 二次函数 在 范围内的最大值是
A. B. C. D.
6. 抛物线 通过变换可以得到抛物线 ,以下变换过程正确的是
A. 先向右平移 个单位,再向上平移 个单位
B. 先向左平移 个单位,再向下平移 个单位
C. 先向右平移 个单位,再向下平移 个单位
D. 先向左平移 个单位,再向上平移 个单位
7. 某抛物线 与 轴的两个交点是 和 ,则方程 的两根分别是
A. , B. ,
C. , D. ,
8. 如图,二次函数 的图象与 轴相交于 和 两点,则不等式 的解是
A. B. C. D.
9. 下列函数中,不是二次函数的是
A. B.
C. D.
10. 已如点 ,, 在二次函数 的图象上,则 ,, 的大小关系是
A. B. C. D.
11. 如图,正方形四个顶点的坐标依次为 ,,,.若抛物线 的图象与正方形有公共点,则实数 的取值范围是
A. B. C. D.
二、填空题(共5小)
12. 若点 , 是二次函数 图象上的两点,那么 与 的大小关系是 .(填 , 或 )
13. 如果抛物线 与 轴交于点 ,那么点 关于此抛物线对称轴的对称点坐标是 .
14. 二次函数 的图象的对称轴是 ,在对称轴的左侧,抛物线从左到右 ;在对称轴的右侧,抛物线从左到右 .
15. 抛物线和 形状相同,方向相反,且顶点为 ,则它的关系式为 .
16. 将二次函数 先向左平移 个单位长度,再向上平移 个单位长度,得到二次函数 的图象,则 , , .
三、解答题(共5小题)
17. 在同一平面直角坐标系中,画出下面函数的图象,并尽可能多地指出两个图象间的共同点、不同点.
();
().
18. 用配方法把二次函数 化为 的形式,并指出这个函数图象的开口方向、对称轴和顶点坐标.
19. 定义:函数图象上到两坐标轴的距离都不大于 的点叫做这个函数图象的“ 阶方点”.例如,点 是函数 图象的“ 阶方点”;点 是函数 图象的“ 阶方点”.
(1)在① ;② ;③ 三点中,是反比例函数 图象的“ 阶方点”的有 (填序号);
(2)若 关于 的一次函数 图象的“ 阶方点”有且只有一个,求 的值;
(3)若 关于 的二次函数 图象的“ 阶方点”一定存在,请直接写出 的取值范围.
20. 已知抛物线 经过 ,, 三点,对称轴是直线 .关于 的方程 有两个相等的实数根.
(1)求抛物线的解析式;
(2)若 ,试比较 与 的大小;
(3)若 , 两点在直线 的两侧,且 ,求 的取值范围.
21. 用“描点法”分别画出下列各函数的图象.
(1).
解:函数 的自变量 的取值范围是 .
(2).
解:函数 的自变量 的取值范围是 .
当函数 的自变量 的取值范围变为 时,请在下图中标出相应的图象.
(3).
解:函数 的自变量 的取值范围是 .
从图象可以得到,函数图象的最低点的坐标是 ;此图象关于 对称.
(4).
解:函数 的自变量 的取值范围是 .
从图象可以得到,此图象关于 对称.
答案
一 单选题
1. C
【解析】过 点作 于 ,
,,
,
,
,,
四边形 为平行四边形,
,
,
,
设 ,,则 ,
,
,
,当 时 ,
故符合解析式的图象为:
故选:C.
2. C
3. B
【解析】直线的解析式为 ,
设 平行于 轴,与一次函数图象交于点
则 ,,
,
,
当 时, 最大为 .
故选:B.
4. B
5. D
【解析】,
对称轴为直线 ,
在 的取值范围内,当 时,有最大值 ,
故选:D.
6. D
7. D
【解析】抛物线与 轴的交点坐标的横坐标即为 的两根,
两个交点是 和 ,
两根分别是 ,.
故选:D.
8. B
9. D
10. C
11. A
【解析】设抛物线的解析式为 ,
当抛物线经过 时,,
当抛物线经过 时,,
观察图象可知 .
故选:A.
二 填空题
12.
13.
【解析】 抛物线 与 轴交于点 坐标为 ,对称轴为 ,
,
点 与此抛物线对称轴的对称点坐标是 .
14. ,上升,下降
15.
【解析】 抛物线的顶点坐标 ,开口方向与抛物线 的方向相反,
这个二次函数的解析式为 .
16. ,,
【解析】将二次函数 先向左平移 个单位长度,再向上平移 个单位长度,
得到二次函数 的图象,即 ,
,,.
,,.
故答案是:;;.
三 解答题
17. 略
18. ,
,
.
开口方向:向上.
顶点坐标:.
对称轴:直线 .
19. (1) ②③
【解析】① 到两坐标轴的距离分别是 ,,
所以 不是反比例函数 图象的“ 阶方点”;
② 到两坐标轴的距离分别是 ,,
所以 是反比例函数 图象的“ 阶方点”;
③ 到两坐标轴的距离分别是 ,,
所以 是反比例函数 图象的“ 阶方点”;
故答案为:②③.
(2) 因为 ,
所以函数经过定点 ,
在以 为中心,边长为 的正方形 中,当直线与正方形区域只有唯一交点时,图象的“ 阶方点”有且只有一个,
由图可知,,,
因为一次函数 图象的“ 阶方点”有且只有一个,
当直线经过点 时,,此时图象的“ 阶方点”有且只有一个,
当直线经过点 时,,此时图象的“ 阶方点”有且只有一个,
综上所述: 的值为 或 ;
(3)
【解析】在以 为中心,边长为 的正方形 中,当抛物线与正方形区域有公共部分时,二次函数 图象的“ 阶方点”一定存在,
如图,
当 时,,,,,
当抛物线经过点 时,(舍)或 ,
当抛物线经过点 时,;
所以 时,二次函数 图象有“ 阶方点”;
综上所述: 时,二次函数 图象有“ 阶方点”一定存在.
20. (1) 抛物线 经过 ,
对称轴是直线 ,
关于 的方程 有两个相等的实数根,
由 可得:
抛物线的解析式为 .
(2) ,
,,
点 ,点 在对称轴直线 的左侧,
抛物线 ,
,即 随 的增大而增大,
,
,
.
(3) 若点 在对称轴直线 的左侧,点 在对称轴直线 的右侧时,
由题意可得
,
若点 在对称轴直线 的左侧,点 在对称轴直线 的右侧时,
由题意可得:
不等式组无解,
综上所述:.
21. (1) 为全体实数,表略,图象略.
(2) 为全体实数,表略,图象略.
(3) 为全体实数,表略,图象略.
; 轴
(4) ,表略,图象略,
原点
同课章节目录
