相似三角形的复习
图片预览






文档简介
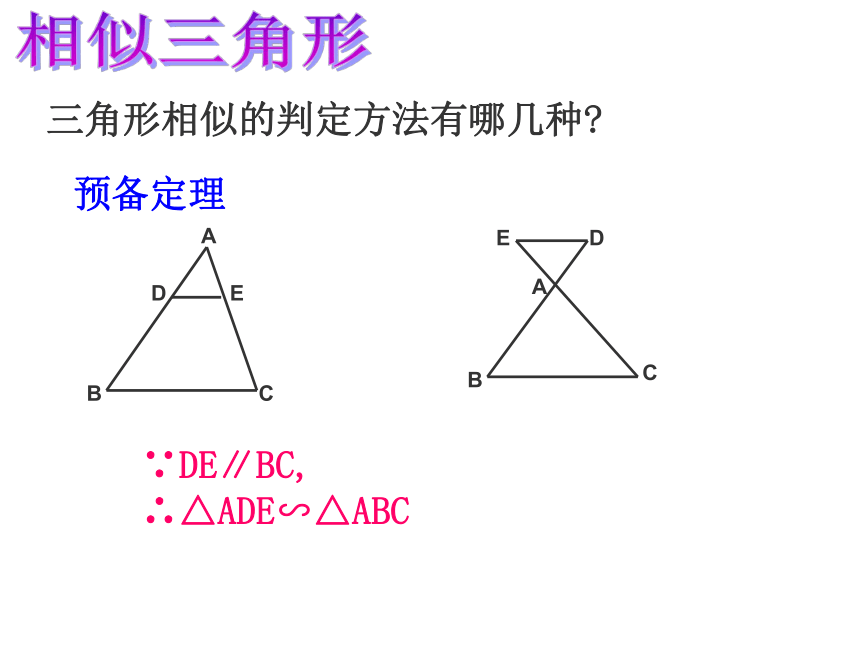
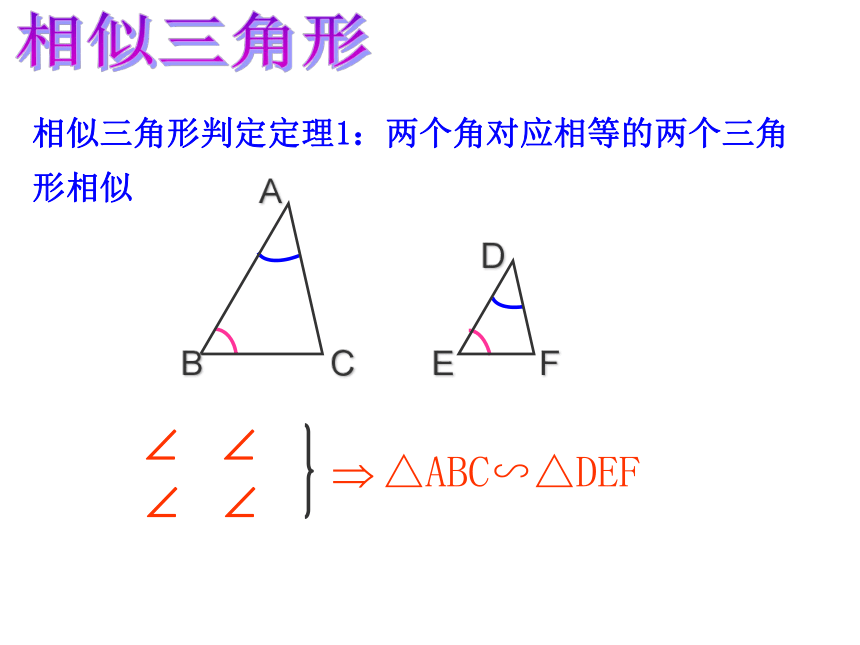
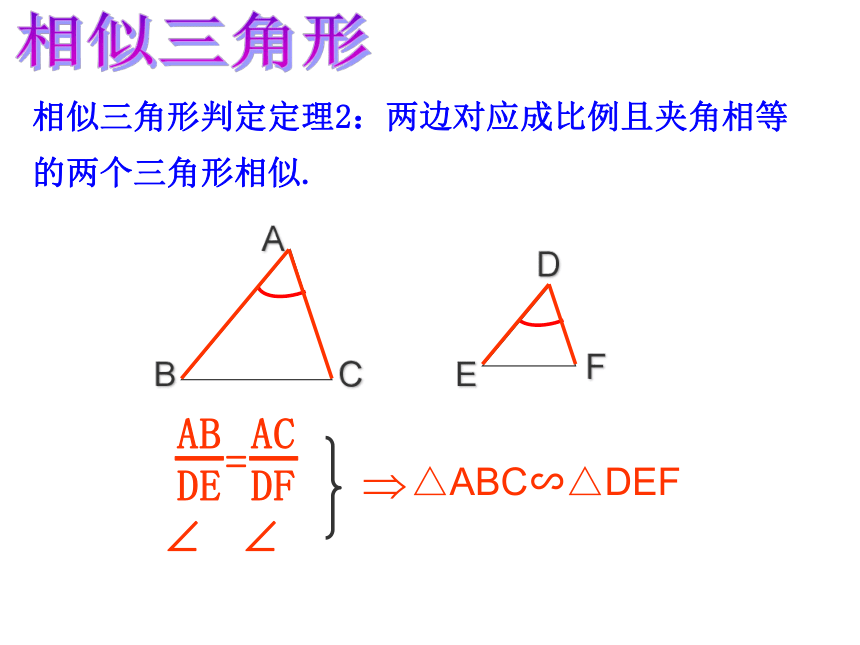
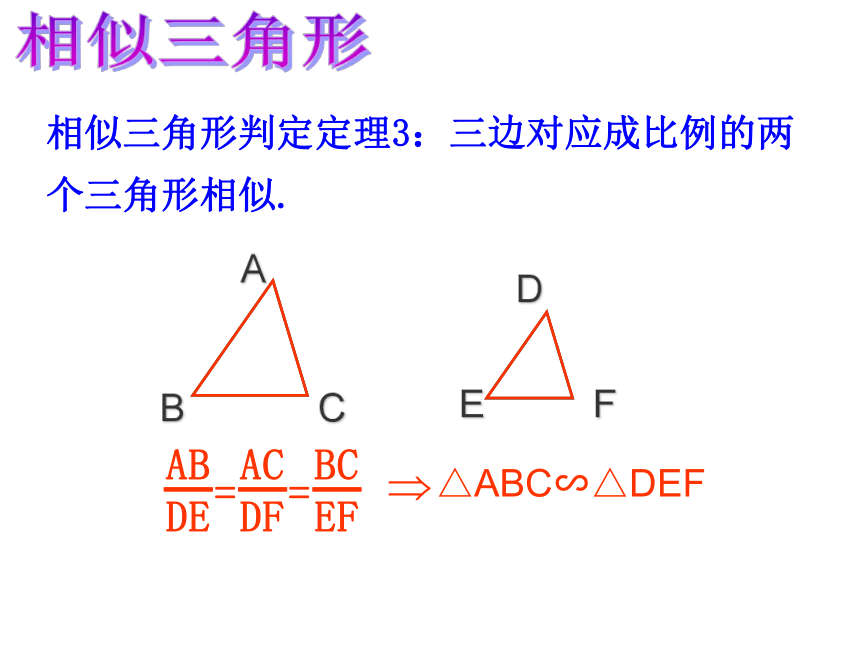
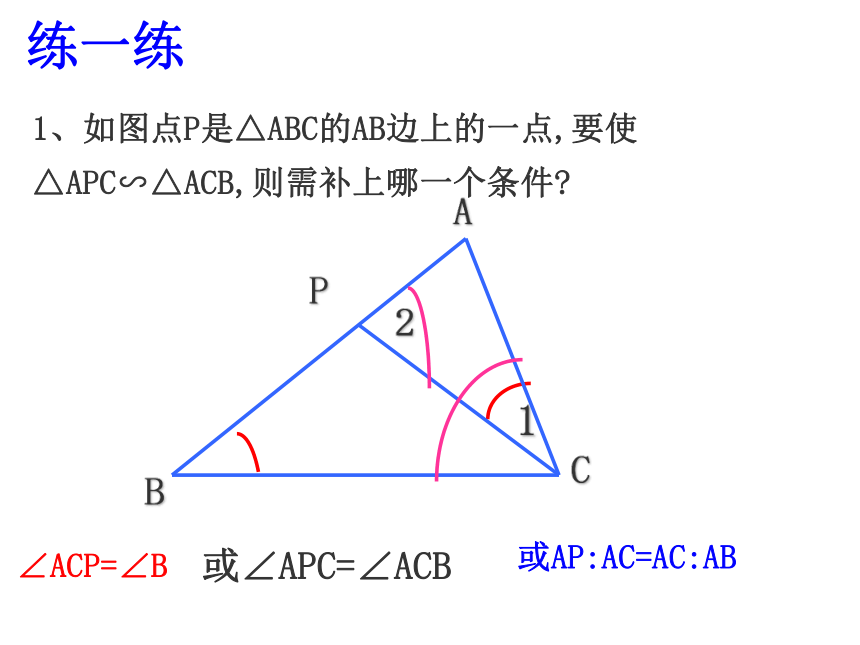
课件36张PPT。第四章 相似三角形复习课比例中项:黄金分割:比例的定义知识回顾4练习:3、计算:定义:对应角相等、对应边成比例的三角形叫做相似三角形。相似比:相似三角形的对应边的比,叫做相似三角形的相似比。相似三角形三角形相似的判定方法有哪几种?预备定理∵DE∥BC, ∴△ADE∽△ABC相似三角形相似三角形判定定理1:两个角对应相等的两个三角形相似相似三角形相似三角形判定定理2:两边对应成比例且夹角相等的两个三角形相似.相似三角形相似三角形判定定理3:三边对应成比例的两个三角形相似.△ABC∽△DEF相似三角形相似三角形的判定:(1)平行于三角形一边的直线截其它两边(或两边的延长线)相交;(2)两角对应相等;(3)两边对应成比例且夹角相等;(4)三边对应成比例;(5)Rt 中被斜边上的高分成的两个三角形相似。练习:4相似三角形相似三角形的性质:1、相似三角形的对应角相等,对应边成比例2、相似三角形的周长比等于相似比,对应高的比
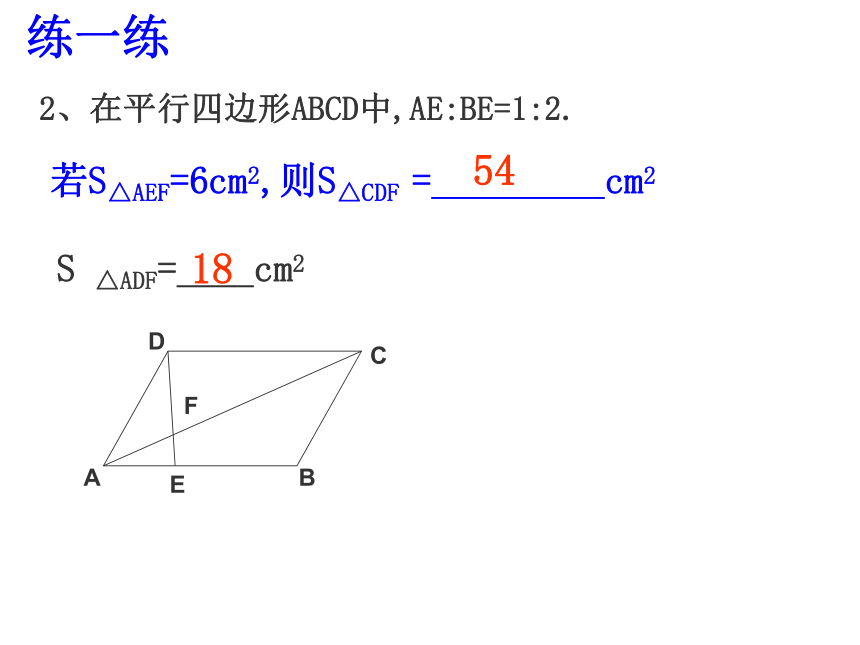
等于相似比3、相似三角形的面积比等于相似比的平方相似三角形或AP:AC=AC:AB练一练1、如图点P是△ABC的AB边上的一点,要使△APC∽△ACB,则需补上哪一个条件?2、在平行四边形ABCD中,AE:BE=1:2.若S△AEF=6cm2,则S△CDF = cm254S △ADF=____cm218练一练3、 如图D,E分别AB,AC是上的点, ∠AED=72o,
∠A=58o,∠B=50o, 那么△ADE和△ABC相似吗?若AE=2,AC=4,则BC是DE的 倍.练一练4、若△ ACP∽△ABC,AP=4,BP=5,则AC=_______,△ ACP与△ABC的相似比是_______,周长之比是_______,面积之比是_______。62 : 32 : 3练一练4 : 95、如图:已知∠ABC=∠CDB=90°,AC=5cm,BC=3cm,当BD取多少cm时 △ABC和△BDC相似?46、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2,
在AC上取一点F,使以A、E、F为顶点的三角形与
△ABC相似,那么AF=________练一练7、 如图, 在直角梯形中, ∠BAD=∠D=∠ACB=90。,
CD= 4, AB= 9, 则 AC=______6例1、如图,正方形ABCD中,E是DC中点,FC= BC.
求证: AE⊥EF证明:∵四边形ABCD是正方形∴BC=CD=AD,∠D=∠C=90°∵E是BC中点,FC= BC∴∴∴△ADE∽△ECF∴∠1=∠2∵∠D=90°∴∠1+ ∠3=90 °∴∠2+ ∠3=90°∴ AE⊥EF例2、如图,DE∥BC,EF∥AB,且S△ADE=25,S△CEF=36.
求△ABC的面积.解:∵DE∥BC,EF∥AB∴∠A=∠CEF,∠AED=∠C∴△ADE∽△EFC∴∵DE∥BC∴△ADE∽△ABC∵ S△ADE=25∴S △ABC=121∴∴∴例3、如图,⊙O是△ABC的外接圆,AB=AC.
求证:AB2=AE·AD证明:连接BD∵AB=AC∴∠ADB=∠ABE又∵∠BAD=∠EAB∴△ABC∽△AEB∴∴AB2=AE·AD例4、如图, 在△ABC中,∠ACB= 900,四边形BEDC为正方形, AE交BC于F, FG∥AC交AB于G. 求证: FC=FG. 证明: ∵四边形BEDC为正方形∴CF∥DE ,DE=BE ∴△ACF∽△ADE∴ ①又∵FG ∥AC∥BE∴△AGF∽△ABE∴ ②由①②可得:又∵ DE=BE∴FC=FG例5、如图,已知:DE ∥BC,DC和BE相交于P点,连结AP交DE于M,延长AP交BC于N点,求证:DM=ME,BN=NC。分析:∽同理可证:BN=NC例6、如图, AB/AD=BC/DE=AC/AE.
(1) 求证: ∠BAD= ∠CAE;
(2) 若已知 AB=6, BD=3, AC=4, 求 CE 的长.(1) ∵ 得∴ΔABC∽ΔADE ∴ ∠BAC=∠DAE∴ ∠BAC-∠DAC=∠DAE-∠DAC 即∠BAD=∠CAE(2) 由∴∵∠BAD=∠CAE ∴ΔABD∽ΔACE∴∴ 证明: 1、如图, 已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP. 试问在射线BF上是否存在一点E,使以点B、E、C为顶点的三角形与△ABP相似?若存在,请求出BE的长;若不存在,请说明理由.FEE做一做做一做2、在?ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,经几秒钟?BPQ与?BAC相似?3、如图,点C,D在线段AB上, △PCD是等边三角形.
(1)当AC,CD,DB满足怎样关系时, △PCA∽△BDP.
(2)当△PCA∽ △BDP时,求∠APB的度数.做一做4、如图,已知△ABC中,BC=8cm,AB=AC=5cm,一动点P在底边上从B点向C点以0.25cm/s的速度移动,当点P运动到和腰垂直的位置时,求P点的运动时间t.DD做一做画一画 在方格纸中,每个小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.在如图4×4的格纸中, △ABC是一个格点三角形(1)在右图中,请你画一个格点三角形,使它与△ABC相似(相似比不为1)(2)在右图中,请你再画一个格点三角形,使它与△ABC相似(相似比不为1),但与图1中所画的三角形大小不一样.相似三角形性质应用2. 如图, AD⊥BC, D为垂足, AD=8, BC=10, EFGH是△ABC内接矩形,(H、G是BC上的两个动点,但H不到达点B, G不到达点C) 设 EH=x,EF=y
(1)求y与x之间的函数关系式,并求自变量x的取值范围;
(2)当EF+EH=9时,求矩形EFGH的周长和面积.相似三角形性质应用相似三角形性质应用 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°(1)求证:△ABD∽△DCE(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值(3)当△ADE是等腰三角形时,求AE的长拓展提高1 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°(1)求证:△ABD∽△DCE∵∠ADC是△ABD的外角∴∠ADC=∠ADE+∠2=∠B+∠1)21证明:∵AB=AC,∠BAC=90°∴∠B=∠C=45°又∵∠ADE=45°∴∠ADE=∠B∴∠1=∠2∴ △ABD∽△DCE(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值解:∵△ABD∽△DCE1∴∴∴ 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°(3)当△ADE是等腰三角形时,求AE的长AD=AEAE=DEDE=AD 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°1分类讨论2、如图,在直角梯形ABCD中,AB∥CD, ∠A=900,AB=2, AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.(1)△ABP与△DPE是否相似?请说明理由;(2)设AP=x DE=y,求y与x之间的函数关系式,并指出自变量x的取值范围;(3)请你探索在点P运动的过程中,四边形ABED能否构成矩形?如果能,求出AP的长;如果不能,请说明理由;(4)请你探索在点P运动的过程中,△BPE能否成为等腰三角形?如果能,求出AP的长,如果不能,请说明理由。25xy5-x拓展提高
等于相似比3、相似三角形的面积比等于相似比的平方相似三角形或AP:AC=AC:AB练一练1、如图点P是△ABC的AB边上的一点,要使△APC∽△ACB,则需补上哪一个条件?2、在平行四边形ABCD中,AE:BE=1:2.若S△AEF=6cm2,则S△CDF = cm254S △ADF=____cm218练一练3、 如图D,E分别AB,AC是上的点, ∠AED=72o,
∠A=58o,∠B=50o, 那么△ADE和△ABC相似吗?若AE=2,AC=4,则BC是DE的 倍.练一练4、若△ ACP∽△ABC,AP=4,BP=5,则AC=_______,△ ACP与△ABC的相似比是_______,周长之比是_______,面积之比是_______。62 : 32 : 3练一练4 : 95、如图:已知∠ABC=∠CDB=90°,AC=5cm,BC=3cm,当BD取多少cm时 △ABC和△BDC相似?46、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2,
在AC上取一点F,使以A、E、F为顶点的三角形与
△ABC相似,那么AF=________练一练7、 如图, 在直角梯形中, ∠BAD=∠D=∠ACB=90。,
CD= 4, AB= 9, 则 AC=______6例1、如图,正方形ABCD中,E是DC中点,FC= BC.
求证: AE⊥EF证明:∵四边形ABCD是正方形∴BC=CD=AD,∠D=∠C=90°∵E是BC中点,FC= BC∴∴∴△ADE∽△ECF∴∠1=∠2∵∠D=90°∴∠1+ ∠3=90 °∴∠2+ ∠3=90°∴ AE⊥EF例2、如图,DE∥BC,EF∥AB,且S△ADE=25,S△CEF=36.
求△ABC的面积.解:∵DE∥BC,EF∥AB∴∠A=∠CEF,∠AED=∠C∴△ADE∽△EFC∴∵DE∥BC∴△ADE∽△ABC∵ S△ADE=25∴S △ABC=121∴∴∴例3、如图,⊙O是△ABC的外接圆,AB=AC.
求证:AB2=AE·AD证明:连接BD∵AB=AC∴∠ADB=∠ABE又∵∠BAD=∠EAB∴△ABC∽△AEB∴∴AB2=AE·AD例4、如图, 在△ABC中,∠ACB= 900,四边形BEDC为正方形, AE交BC于F, FG∥AC交AB于G. 求证: FC=FG. 证明: ∵四边形BEDC为正方形∴CF∥DE ,DE=BE ∴△ACF∽△ADE∴ ①又∵FG ∥AC∥BE∴△AGF∽△ABE∴ ②由①②可得:又∵ DE=BE∴FC=FG例5、如图,已知:DE ∥BC,DC和BE相交于P点,连结AP交DE于M,延长AP交BC于N点,求证:DM=ME,BN=NC。分析:∽同理可证:BN=NC例6、如图, AB/AD=BC/DE=AC/AE.
(1) 求证: ∠BAD= ∠CAE;
(2) 若已知 AB=6, BD=3, AC=4, 求 CE 的长.(1) ∵ 得∴ΔABC∽ΔADE ∴ ∠BAC=∠DAE∴ ∠BAC-∠DAC=∠DAE-∠DAC 即∠BAD=∠CAE(2) 由∴∵∠BAD=∠CAE ∴ΔABD∽ΔACE∴∴ 证明: 1、如图, 已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP. 试问在射线BF上是否存在一点E,使以点B、E、C为顶点的三角形与△ABP相似?若存在,请求出BE的长;若不存在,请说明理由.FEE做一做做一做2、在?ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,经几秒钟?BPQ与?BAC相似?3、如图,点C,D在线段AB上, △PCD是等边三角形.
(1)当AC,CD,DB满足怎样关系时, △PCA∽△BDP.
(2)当△PCA∽ △BDP时,求∠APB的度数.做一做4、如图,已知△ABC中,BC=8cm,AB=AC=5cm,一动点P在底边上从B点向C点以0.25cm/s的速度移动,当点P运动到和腰垂直的位置时,求P点的运动时间t.DD做一做画一画 在方格纸中,每个小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.在如图4×4的格纸中, △ABC是一个格点三角形(1)在右图中,请你画一个格点三角形,使它与△ABC相似(相似比不为1)(2)在右图中,请你再画一个格点三角形,使它与△ABC相似(相似比不为1),但与图1中所画的三角形大小不一样.相似三角形性质应用2. 如图, AD⊥BC, D为垂足, AD=8, BC=10, EFGH是△ABC内接矩形,(H、G是BC上的两个动点,但H不到达点B, G不到达点C) 设 EH=x,EF=y
(1)求y与x之间的函数关系式,并求自变量x的取值范围;
(2)当EF+EH=9时,求矩形EFGH的周长和面积.相似三角形性质应用相似三角形性质应用 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°(1)求证:△ABD∽△DCE(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值(3)当△ADE是等腰三角形时,求AE的长拓展提高1 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°(1)求证:△ABD∽△DCE∵∠ADC是△ABD的外角∴∠ADC=∠ADE+∠2=∠B+∠1)21证明:∵AB=AC,∠BAC=90°∴∠B=∠C=45°又∵∠ADE=45°∴∠ADE=∠B∴∠1=∠2∴ △ABD∽△DCE(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值解:∵△ABD∽△DCE1∴∴∴ 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°(3)当△ADE是等腰三角形时,求AE的长AD=AEAE=DEDE=AD 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°1分类讨论2、如图,在直角梯形ABCD中,AB∥CD, ∠A=900,AB=2, AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.(1)△ABP与△DPE是否相似?请说明理由;(2)设AP=x DE=y,求y与x之间的函数关系式,并指出自变量x的取值范围;(3)请你探索在点P运动的过程中,四边形ABED能否构成矩形?如果能,求出AP的长;如果不能,请说明理由;(4)请你探索在点P运动的过程中,△BPE能否成为等腰三角形?如果能,求出AP的长,如果不能,请说明理由。25xy5-x拓展提高
同课章节目录
