1.2锐角三角函数的计算 课件(共26张PPT) 2022—2023学年浙教版数学九年级下册
文档属性
| 名称 | 1.2锐角三角函数的计算 课件(共26张PPT) 2022—2023学年浙教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
1.2锐角三角函数的计算
教学目标
1.复习并巩固锐角三角函数的相关知识.
2.学会利用计算器求三角函数值并进行相关计算.
3.学会利用计算器根据三角函数值求锐角度数并计算.
新知导入
已知圆弧形公路弯道的两端相距200m,圆弧半径为1km,你能求出弯道的长吗?
新知讲解
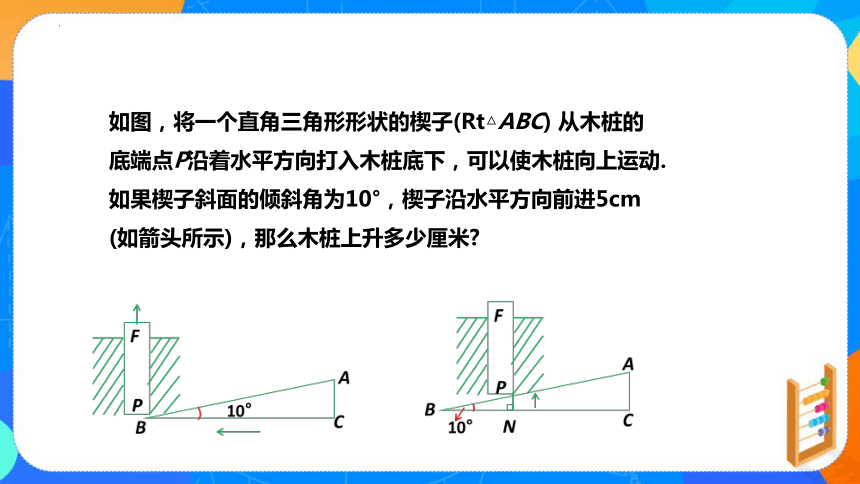
如图,将一个直角三角形形状的楔子(Rt△ABC) 从木桩的
底端点P沿着水平方向打入木桩底下,可以使木桩向上运动.
如果楔子斜面的倾斜角为10°,楔子沿水平方向前进5cm
(如箭头所示),那么木桩上升多少厘米
新知讲解
分数有意义的条件是分母不为0.
10°
F
P
A
B
C
N
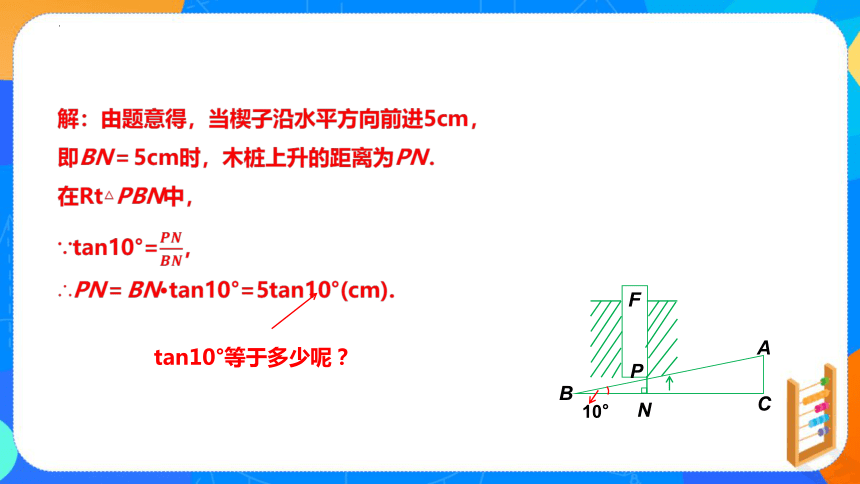
解:由题意得,当楔子沿水平方向前进5cm,
即BN=5cm时,木桩上升的距离为PN.
在Rt△PBN中,
∵tan10°=,
∴PN=BN·tan10°=5tan10°(cm).
tan10°等于多少呢?
新知讲解
前面我们学习了特殊角30°,45°,60°的三角函数值,那么一些非特殊角(如10°,56°,89°等)的三角函数值又怎么求呢
利用计算器求锐角三角函数值
新知讲解
请按下表内的按键顺序,求相应的三角函数值.
按键顺序 显示结果
sin30° sin 3 0 = 0.5
cos55° cos 5 5 = 0.5735764364
tan86°17' tan 8 6 ° 1 7 ° = 15.39427604
sin68°28'32″ sin 6 8 ° 2 8 ° 3 2 ° = 0.93026112
cos21.5° cos 2 1 . 5 = 0.930417568
新知讲解
计算器的型号不同,按键方法也不一定相同.另
外当我们计算以度分秒为单位的数据时,一般化成以
度为单位来进行计算.
典例精析
例1 如图,在Rt△ABC中,∠C=90°,AB=12cm,∠A=35°.求△ABC的周长和面积(周长精确到0.1cm,
面积精确到0.1cm2).
解:在Rt△ABC中,
∵sinA=,cosA=,
∴BC=AB sinA,AC=AB cosA.
∴ △ABC的周长=AB+BC+AC
C
A
B
新知讲解
=AB+AB sinA+AB cosA
=AB(1+sinA+cosA)
=12(1+sin35°+cos35°)
≈28.7(cm);
按键顺序:
1
2
(
1
+
sin
3
5
)
+
cos
3
5
)
)
=
△ABC的面积
= AC BC= AB cosA AB sinA
典例精析
= AB2 sinA cosA
= ×122×sin35° cos35°
≈33.8(cm2).
按键顺序:
1
÷
2
×
1
2
x2
×
sin
3
5
)
×
cos
3
5
)
=
答: △ABC的周长约为28.7cm,
面积约为33.8cm2.
新知讲解
如图,为了方便行人,市政府在10m高的天桥两端修建了40m长的斜道.这条斜道的倾斜角是多少?
新知讲解
已知一个角的三角函数值,求这个角的度数,这类问题可以通过计算器来解决,此时用到“”,“”,“”键的第二功能“”,“”,“”.
例如:已知,求锐角.按健顺序为:
如果再按“度分秒键 ”,就换算成“度分秒”的形式,
即α=17°18′5.43″.
典例精析
例2 根据下面的条件,求锐角β的大小(精确到1″).
(1)sin β=0.4511; (2)cosβ=0.7857; (3)tan β=1.4036.
解 (1)按键顺序为:
SHIFT
sin-1
0
4
5
1
1
=
°′″
得β≈26°48′51″.
(2)按键顺序为:
SHIFT
cos-1
0
7
8
5
7
=
°′″
得β≈38°12′52″.
典例精析
(3)按键顺序为:
SHIFT
tan-1
1
4
0
3
6
=
°′″
得β≈54°31′55″.
典例精析
A
B
R
例2 如图,一段公路弯道呈圆弧形,测得弯道两端的
距离为200m, 的半径为1000m.求弯道的长(精确到0.1m).
O
∴∠AOB≈11.48°,∴ =≈200.3m.
答:弯道的长约为200.3m.
解:作OC⊥AB,垂足为C,则OC平分∠AOB.
在Rt△OCB中,BC=AB=100m,OB=1000m,
∴sin∠BOC=.
利用计算器求得∠BOC=5°44′21.01″,
C
课堂练习
【知识技能类作业】必做题:
1. 用计算器求sin24°37′18″的值,以下按键顺序正确的是 ( )
A.
B.
C.
D.
A
sin
2
4
D.M′S
3
7
D.M′S
8
1
D.M′S
=
sin
2
4
D.M′S
3
7
D.M′S
8
1
D.M′S
=
2nd F
sin
2
4
D.M′S
8
1
D.M′S
=
sin
2
4
D.M′S
3
7
D.M′S
8
1
D.M′S
=
2nd F
课堂练习
【知识技能类作业】必做题:
2. 下列式子中,不成立的是 ( )
A.sin35°= cos55°
B.sin30°+ sin45°= sin75°
C. cos30°= sin60°
D.sin260°+ cos260°=1
3.用计算器计算cos 44°的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
B
B
课堂练习
【知识技能类作业】选做题:
4.下列各式中一定成立的是( )
A.tan75°﹥tan48°﹥tan15° B. tan75°﹤tan48°﹤tan15°
C. cos75°﹥cos48°﹥cos15° D. sin75°﹤sin48°5.已知α为锐角,且tan α=3.387,下列各值中与α最接近的是( )
A.73°33′ B.73°27′
C.16°27′ D.16°21′
A
A
课堂练习
【综合拓展类作业】
解:由题意知,tan∠ACD=≈0.5208,
所以∠ACD=27.5°,
即∠ACB=2∠ACD≈2×27.50 =55°.
答:V型角的大小约为55°.
5、如图,工件上有一V型槽,测得它的上口AB宽20mm,
深CD=19.2mm. AC=BC,求V型角(∠ACB)的大小(结果精确到1° ).
课堂总结
用计算器求锐角三角函数值及锐角
用计算器求锐角的三角函数值或角的度数
注意:不同的计算器操作步骤可能有所不同
利用计算器探索锐三角函数的新知
板书设计
1.用计算器求锐角的三角函数值
2.已知三角函数值求角的度数
作业布置
【知识技能类作业】必做题:
1.在△ABC中,∠C=90°,BC=5,AB=13,用科学计算器求∠A约等于( )
A.24°38′ B.65°22′ C.67°23′ D.22°37′
2.如图,有一滑梯AB,其水平宽度AC为5.3米,铅直高度BC为2.8米,则∠A的度数约为________(用科学计算器计算,结果精确到0.1°).
D
27.8°
作业布置
【知识技能类作业】必做题:
(1)sin a=0.2476;
(2)cos a=0.4174;
(3)tan a=0.1890.
α≈14°20′
3、已知锐角a的三角函数值,使用计算器求锐角a(精确到1′).
α≈65°20′
α≈10°42′
作业布置
【知识技能类作业】选做题:
4、比较下列各组数的大小:
(1)sin 52°与sin 62°;(2)tan 89°与tan 48°; (3)sin 47°与cos 47°.
解:(1)∵锐角的正弦值随着角度的增大而增大,
∴sin 52°(2)∵锐角的正切值随着角度的增大而增大,
∴ tan 48°<tan 89°.
(3)∵sin 47°=cos (90°-47°)=cos 43°,
而cos 43°>cos 47°,
∴sin 47°>cos 47°.
作业布置
【综合拓展类作业】
5、如图,为了测量一条河的宽度,一测量员在河岸边的
C处测得对岸一棵树A在正南方向,测量员向正东方向走180米到点B处,测得这棵树在南偏西68°的方向,
求河的宽度(结果保留四个有效数字).
C
B
A
北
东
解:在Rt△ABC中,BC=180m,∠A=68°.
∴AC= ≈77.72m.
答:河的宽度约为77.72m.
1.2锐角三角函数的计算
教学目标
1.复习并巩固锐角三角函数的相关知识.
2.学会利用计算器求三角函数值并进行相关计算.
3.学会利用计算器根据三角函数值求锐角度数并计算.
新知导入
已知圆弧形公路弯道的两端相距200m,圆弧半径为1km,你能求出弯道的长吗?
新知讲解
如图,将一个直角三角形形状的楔子(Rt△ABC) 从木桩的
底端点P沿着水平方向打入木桩底下,可以使木桩向上运动.
如果楔子斜面的倾斜角为10°,楔子沿水平方向前进5cm
(如箭头所示),那么木桩上升多少厘米
新知讲解
分数有意义的条件是分母不为0.
10°
F
P
A
B
C
N
解:由题意得,当楔子沿水平方向前进5cm,
即BN=5cm时,木桩上升的距离为PN.
在Rt△PBN中,
∵tan10°=,
∴PN=BN·tan10°=5tan10°(cm).
tan10°等于多少呢?
新知讲解
前面我们学习了特殊角30°,45°,60°的三角函数值,那么一些非特殊角(如10°,56°,89°等)的三角函数值又怎么求呢
利用计算器求锐角三角函数值
新知讲解
请按下表内的按键顺序,求相应的三角函数值.
按键顺序 显示结果
sin30° sin 3 0 = 0.5
cos55° cos 5 5 = 0.5735764364
tan86°17' tan 8 6 ° 1 7 ° = 15.39427604
sin68°28'32″ sin 6 8 ° 2 8 ° 3 2 ° = 0.93026112
cos21.5° cos 2 1 . 5 = 0.930417568
新知讲解
计算器的型号不同,按键方法也不一定相同.另
外当我们计算以度分秒为单位的数据时,一般化成以
度为单位来进行计算.
典例精析
例1 如图,在Rt△ABC中,∠C=90°,AB=12cm,∠A=35°.求△ABC的周长和面积(周长精确到0.1cm,
面积精确到0.1cm2).
解:在Rt△ABC中,
∵sinA=,cosA=,
∴BC=AB sinA,AC=AB cosA.
∴ △ABC的周长=AB+BC+AC
C
A
B
新知讲解
=AB+AB sinA+AB cosA
=AB(1+sinA+cosA)
=12(1+sin35°+cos35°)
≈28.7(cm);
按键顺序:
1
2
(
1
+
sin
3
5
)
+
cos
3
5
)
)
=
△ABC的面积
= AC BC= AB cosA AB sinA
典例精析
= AB2 sinA cosA
= ×122×sin35° cos35°
≈33.8(cm2).
按键顺序:
1
÷
2
×
1
2
x2
×
sin
3
5
)
×
cos
3
5
)
=
答: △ABC的周长约为28.7cm,
面积约为33.8cm2.
新知讲解
如图,为了方便行人,市政府在10m高的天桥两端修建了40m长的斜道.这条斜道的倾斜角是多少?
新知讲解
已知一个角的三角函数值,求这个角的度数,这类问题可以通过计算器来解决,此时用到“”,“”,“”键的第二功能“”,“”,“”.
例如:已知,求锐角.按健顺序为:
如果再按“度分秒键 ”,就换算成“度分秒”的形式,
即α=17°18′5.43″.
典例精析
例2 根据下面的条件,求锐角β的大小(精确到1″).
(1)sin β=0.4511; (2)cosβ=0.7857; (3)tan β=1.4036.
解 (1)按键顺序为:
SHIFT
sin-1
0
4
5
1
1
=
°′″
得β≈26°48′51″.
(2)按键顺序为:
SHIFT
cos-1
0
7
8
5
7
=
°′″
得β≈38°12′52″.
典例精析
(3)按键顺序为:
SHIFT
tan-1
1
4
0
3
6
=
°′″
得β≈54°31′55″.
典例精析
A
B
R
例2 如图,一段公路弯道呈圆弧形,测得弯道两端的
距离为200m, 的半径为1000m.求弯道的长(精确到0.1m).
O
∴∠AOB≈11.48°,∴ =≈200.3m.
答:弯道的长约为200.3m.
解:作OC⊥AB,垂足为C,则OC平分∠AOB.
在Rt△OCB中,BC=AB=100m,OB=1000m,
∴sin∠BOC=.
利用计算器求得∠BOC=5°44′21.01″,
C
课堂练习
【知识技能类作业】必做题:
1. 用计算器求sin24°37′18″的值,以下按键顺序正确的是 ( )
A.
B.
C.
D.
A
sin
2
4
D.M′S
3
7
D.M′S
8
1
D.M′S
=
sin
2
4
D.M′S
3
7
D.M′S
8
1
D.M′S
=
2nd F
sin
2
4
D.M′S
8
1
D.M′S
=
sin
2
4
D.M′S
3
7
D.M′S
8
1
D.M′S
=
2nd F
课堂练习
【知识技能类作业】必做题:
2. 下列式子中,不成立的是 ( )
A.sin35°= cos55°
B.sin30°+ sin45°= sin75°
C. cos30°= sin60°
D.sin260°+ cos260°=1
3.用计算器计算cos 44°的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
B
B
课堂练习
【知识技能类作业】选做题:
4.下列各式中一定成立的是( )
A.tan75°﹥tan48°﹥tan15° B. tan75°﹤tan48°﹤tan15°
C. cos75°﹥cos48°﹥cos15° D. sin75°﹤sin48°
A.73°33′ B.73°27′
C.16°27′ D.16°21′
A
A
课堂练习
【综合拓展类作业】
解:由题意知,tan∠ACD=≈0.5208,
所以∠ACD=27.5°,
即∠ACB=2∠ACD≈2×27.50 =55°.
答:V型角的大小约为55°.
5、如图,工件上有一V型槽,测得它的上口AB宽20mm,
深CD=19.2mm. AC=BC,求V型角(∠ACB)的大小(结果精确到1° ).
课堂总结
用计算器求锐角三角函数值及锐角
用计算器求锐角的三角函数值或角的度数
注意:不同的计算器操作步骤可能有所不同
利用计算器探索锐三角函数的新知
板书设计
1.用计算器求锐角的三角函数值
2.已知三角函数值求角的度数
作业布置
【知识技能类作业】必做题:
1.在△ABC中,∠C=90°,BC=5,AB=13,用科学计算器求∠A约等于( )
A.24°38′ B.65°22′ C.67°23′ D.22°37′
2.如图,有一滑梯AB,其水平宽度AC为5.3米,铅直高度BC为2.8米,则∠A的度数约为________(用科学计算器计算,结果精确到0.1°).
D
27.8°
作业布置
【知识技能类作业】必做题:
(1)sin a=0.2476;
(2)cos a=0.4174;
(3)tan a=0.1890.
α≈14°20′
3、已知锐角a的三角函数值,使用计算器求锐角a(精确到1′).
α≈65°20′
α≈10°42′
作业布置
【知识技能类作业】选做题:
4、比较下列各组数的大小:
(1)sin 52°与sin 62°;(2)tan 89°与tan 48°; (3)sin 47°与cos 47°.
解:(1)∵锐角的正弦值随着角度的增大而增大,
∴sin 52°
∴ tan 48°<tan 89°.
(3)∵sin 47°=cos (90°-47°)=cos 43°,
而cos 43°>cos 47°,
∴sin 47°>cos 47°.
作业布置
【综合拓展类作业】
5、如图,为了测量一条河的宽度,一测量员在河岸边的
C处测得对岸一棵树A在正南方向,测量员向正东方向走180米到点B处,测得这棵树在南偏西68°的方向,
求河的宽度(结果保留四个有效数字).
C
B
A
北
东
解:在Rt△ABC中,BC=180m,∠A=68°.
∴AC= ≈77.72m.
答:河的宽度约为77.72m.
