4.2相似三角形(浙江省宁波市)

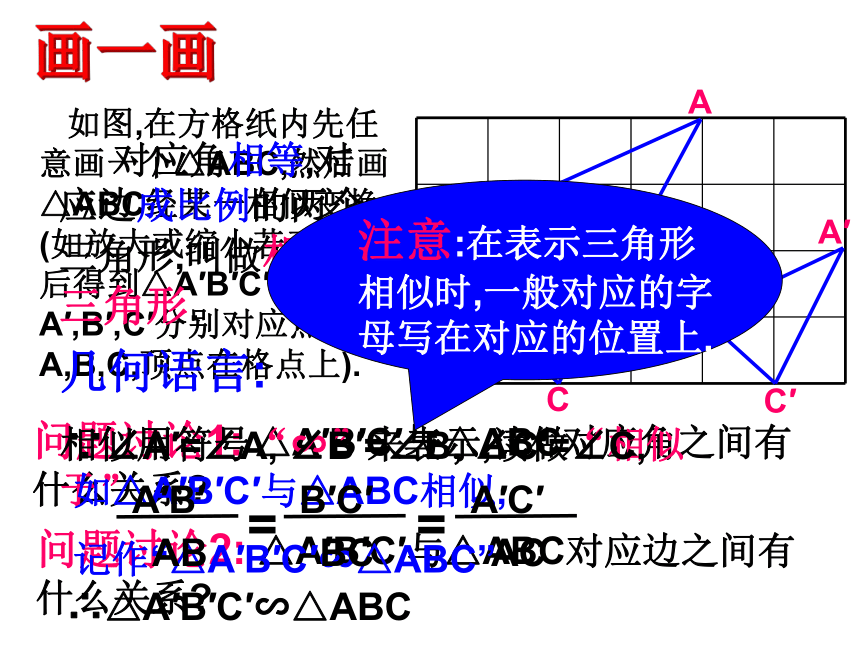
课件18张PPT。4.2 相似三角形观察上图中几幅图形可以通过怎样的图形变换得到？知识回顾相似变换的性质: 图形的相似变换不改变图形中每一个角的大小;图形中的每条线段都扩大(或缩小)相同的倍数. 如图,在方格纸内先任意画一个△ABC,然后画△ABC经某一相似变换(如放大或缩小若干倍)后得到△A′B′C′(点A′,B′,C′分别对应点A,B,C,顶点在格点上).问题讨论1: △A′B′C′与△ABC对应角之间有什么关系?问题讨论2: △A′B′C′与△ABC对应边之间有什么关系?画一画 对应角相等,对应边成比例的两个三角形,叫做相似三角形.相似用符号“∽”来表示,读做“相似于”如△A′B′C′与△ABC相似,
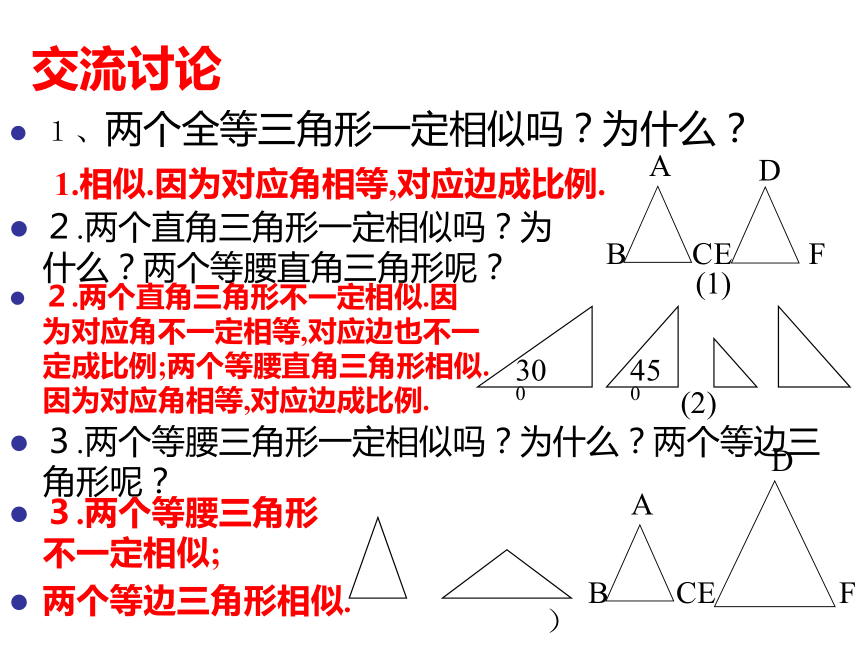
记作“△A′B′C′∽△ABC”几何语言:∴△A′B′C′∽△ABC１、两个全等三角形一定相似吗？为什么？２.两个直角三角形一定相似吗？为什么？两个等腰直角三角形呢？３.两个等腰三角形一定相似吗？为什么？两个等边三角形呢？ 1.相似.因为对应角相等,对应边成比例.２.两个直角三角形不一定相似.因为对应角不一定相等,对应边也不一定成比例;两个等腰直角三角形相似.因为对应角相等,对应边成比例.３.两个等腰三角形不一定相似;
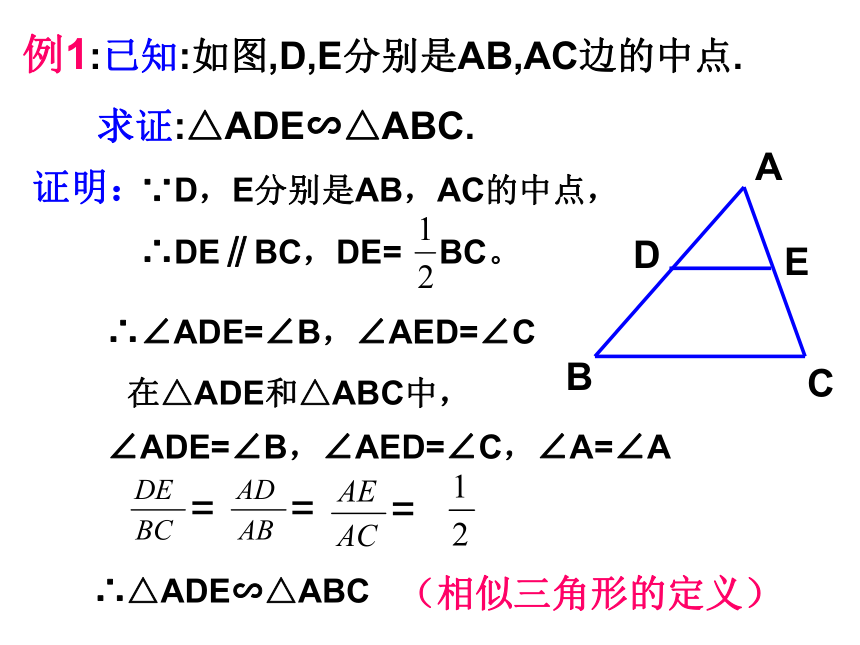
两个等边三角形相似.交流讨论例1:已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.证明：∵D，E分别是AB，AC的中点，∴∠ADE=∠B，∠AED=∠C在△ADE和△ABC中，∠ADE=∠B，∠AED=∠C，∠A=∠A∴DE∥BC，DE= BC。∴△ADE∽△ABC（相似三角形的定义）性质: 相似三角形的对应角相等,对应边成比例. 相似三角形对应边的比,叫做两个相似三角形的相似比(或相似系数) (similitude ratio).则△ABC与△A'B'C'的
相似比k1△A'B'C'与△ABC的相似比k2=？=？ 如果△ABC∽△A'B'C'三角形的前后次序不同，所得相似比不同。求相似比: 如图， △ADE∽ △ABC,点D与点B是对应点，根据图形分别写出两个三角形的对应角和对应边成比例的比例式.（1）做一做例2、已知:如图,D,E分别是△ABC的AB,AC边上的点, △ABC∽△ADE.已知AD﹕DB=1﹕2,BC=9cm,求DE的长.1、在下面的两组图形中,各有两个相似三角形,试确定x ,y ,m ,n 的值. m°50°45°2ay(2)CDEF随堂练习2.如图，D是AB上的一点。 △ABC∽ △ACD ，且AD：AC＝2：3,∠ADC= 65°, ∠B＝43 °.
（1）求∠ABC， ∠ACD的度数；
（2）写出△ABC与 △ACD的对应边成比例的比例式，求出相似比。 2、如图，AB，CD相交于点0, △AOC∽ △BOD 。
（1）如果OC：OD＝1：2,AC＝5,求BD的长；
（2）如果∠A＝35°, ∠AOC＝100°,求∠D的度数。1,已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的最大边为8,求其余两边.已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的一边为8,求其余两边.探究活动4,64,6或12,16或16/3,32/3问题探究：2. 如果△ABC ≌ △ A`B`C` ， △ABC ∽ △DEF，能不能得到 △ A`B`C` ∽ △DEF？3. 如果两个三角形都与第三个三角形相似，那么这两个三角形相似吗？为什么？在方格纸中,每个小格的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图所示,在10×10的方格中,已知△OAB.4-1-143213012A-4-3-2-4-3-2B5-5数学乐园1.作一个格点三角形与△OAB全等.2.作一个格点三角形与△OAB相似.3.作一个格点三角形与△OAB相似且与△OAB 共边AB.●●●●●你说我说大家说 请你谈谈学习本节课后的感受!谢谢指导!
再见！