3.1直线与圆的位置关系(1)
图片预览




文档简介
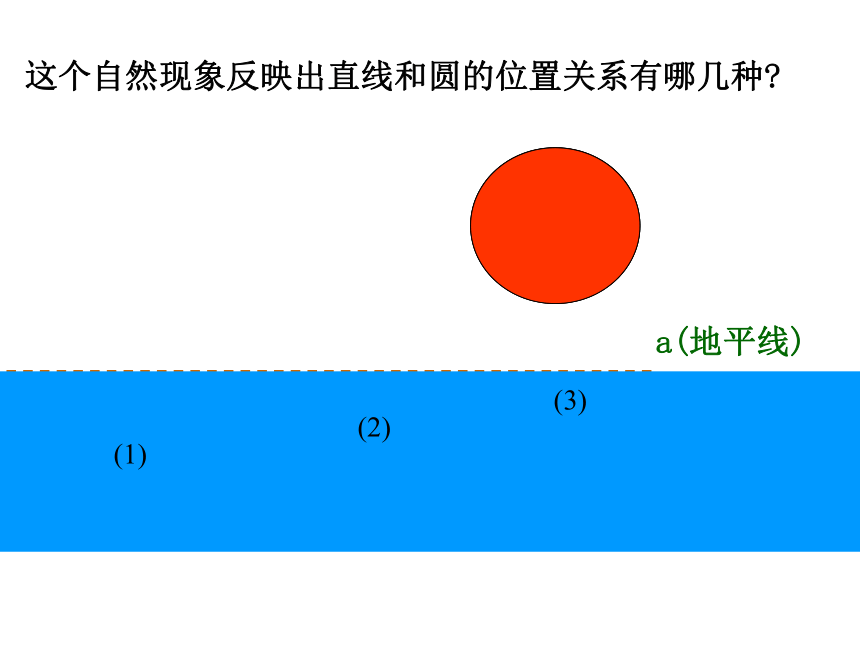
课件25张PPT。点和圆的位置关系有几种?回顾思考直线外一点到这条直线垂线段的长度叫点到直线的距离。什么叫点到直线的距离? 连结直线外一点与直线所有点的线段中,最短的是______; 垂线段请观察,你有什么发现?请观察,你有什么发现?请观察,你有什么发现?a(地平线)这个自然现象反映出直线和圆的位置关系有哪几种?
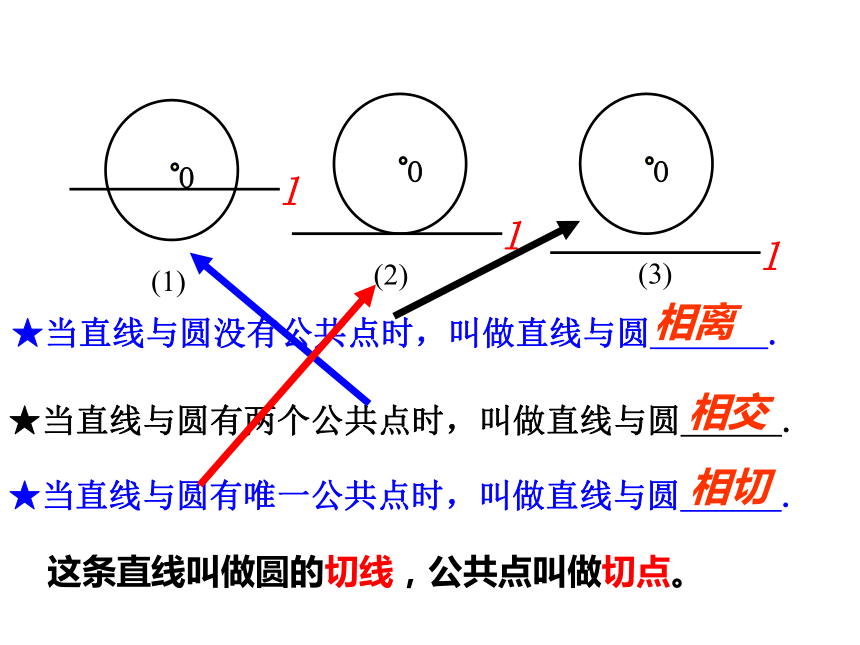
(1)(3)(2) 3.1直线与圆的位置关系(1)★当直线与圆有唯一公共点时,叫做直线与圆 .★当直线与圆没有公共点时,叫做直线与圆 . ★当直线与圆有两个公共点时,叫做直线与圆 . 相离相切相交(1)(3)(2)这条直线叫做圆的切线,公共点叫做切点。OOOlll直线与圆的位置关系有 种.
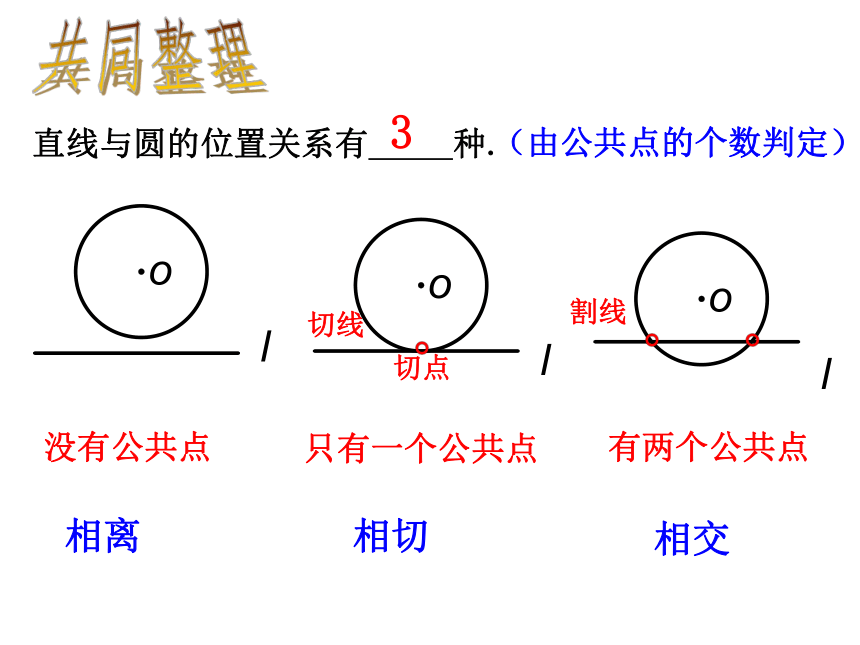
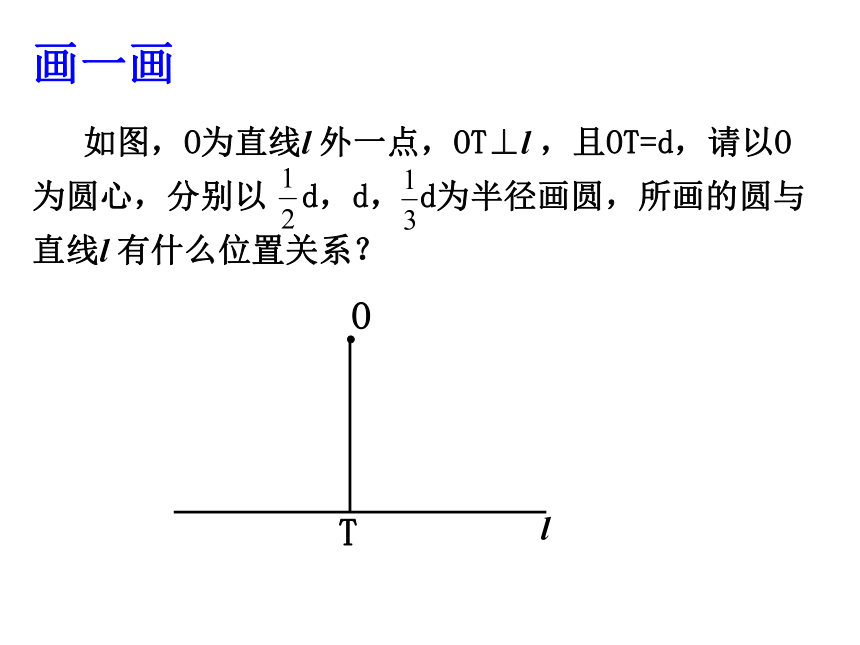
3没有公共点相离只有一个公共点相切切点切线有两个公共点相交割线(由公共点的个数判定)共同整理画一画观察 讨论结合图形,如何由数量关系判定直线与圆的位置关系?d>rd=rdrd=rdrd=rd∴直线l与⊙O相交∵d=r
∴直线l与⊙O相切∵d>r
∴直线l与⊙O相离试一试3、在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,设⊙C的半径为r,请根据r的下列值,判断直线AB与⊙C的位置关系,并说明理由。(2)r =2.4厘米(3)r =3厘米(1)r =2厘米试一试即:圆心C到AB的距离d=2.4cm解:过C作CD⊥AB,垂足为D,则(1) r = 2cm(2)r =2.4cm(3) r =3cm 在Rt△ABC中,根据三角形的面积公式有3、在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,设⊙C的半径为r,请根据r的下列值,判断直线AB与⊙C的位置关系,并说明理由。试一试4、在△ABC 中,∠ACB=90°,AC=3cm,BC=4cm,设⊙C的半径为r。1、当r满足 时,
⊙C与直线AB相离.2、当r满足________时,⊙C与直线AB相切.0cm(1)相交;(2)相切;(3)相离。4、已知圆的直径为13cm,如果一条直线和圆心的距离分别为:(1)d=4.5cm (2)d=6.5cm (3)d=8cm, 那么直线和圆有几个公共点?为什么?练一练1、直线与圆的三种位置关系210dr交点切点无相交相切相离谈谈你本节课有哪些困惑或者收获?2、判定直线与圆的位置关系的方法有____种:(1)由________________ 的个数来判断;(2)由 的数量大小关系来判断.注意:在实际应用中,常采用第二种方法判定.两直线与圆的公共点圆心到直线的距离d与半径r再 见!
(1)(3)(2) 3.1直线与圆的位置关系(1)★当直线与圆有唯一公共点时,叫做直线与圆 .★当直线与圆没有公共点时,叫做直线与圆 . ★当直线与圆有两个公共点时,叫做直线与圆 . 相离相切相交(1)(3)(2)这条直线叫做圆的切线,公共点叫做切点。OOOlll直线与圆的位置关系有 种.
3没有公共点相离只有一个公共点相切切点切线有两个公共点相交割线(由公共点的个数判定)共同整理画一画观察 讨论结合图形,如何由数量关系判定直线与圆的位置关系?d>rd=rd
∴直线l与⊙O相切∵d>r
∴直线l与⊙O相离试一试3、在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,设⊙C的半径为r,请根据r的下列值,判断直线AB与⊙C的位置关系,并说明理由。(2)r =2.4厘米(3)r =3厘米(1)r =2厘米试一试即:圆心C到AB的距离d=2.4cm解:过C作CD⊥AB,垂足为D,则(1) r = 2cm(2)r =2.4cm(3) r =3cm 在Rt△ABC中,根据三角形的面积公式有3、在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,设⊙C的半径为r,请根据r的下列值,判断直线AB与⊙C的位置关系,并说明理由。试一试4、在△ABC 中,∠ACB=90°,AC=3cm,BC=4cm,设⊙C的半径为r。1、当r满足 时,
⊙C与直线AB相离.2、当r满足________时,⊙C与直线AB相切.0cm
