弧长及扇形面积
图片预览






文档简介
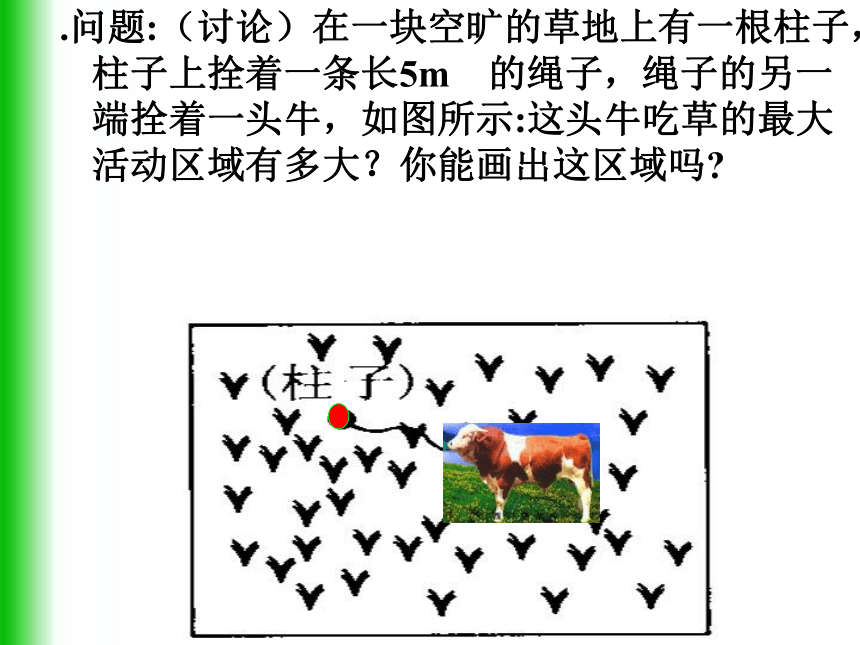
课件31张PPT。弧长和扇形的面积情境导入1:在田径二百米跑比赛中,每位运动员的起跑位置相同吗?每位运动员弯路的展直长度相同吗?情境导入2:.问题:(讨论)在一块空旷的草地上有一根柱子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示:这头牛吃草的最大活动区域有多大?你能画出这区域吗?
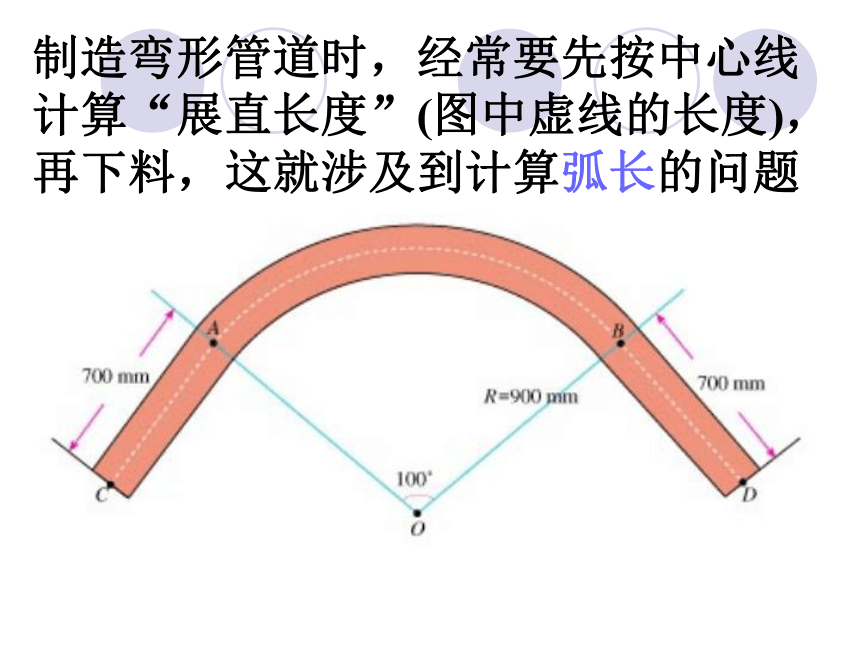
制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线的长度),再下料,这就涉及到计算弧长的问题
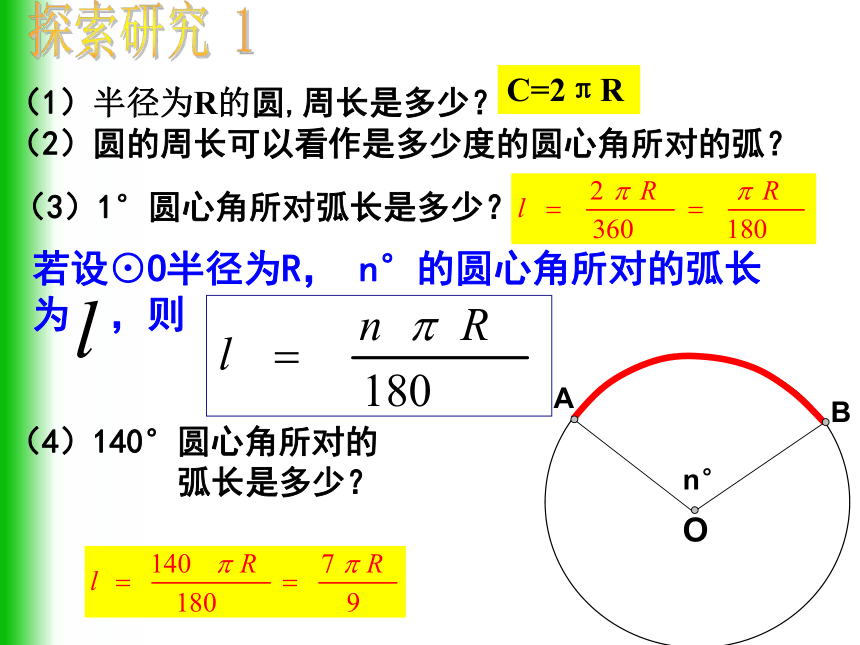
(1)半径为R的圆,周长是多少?C=2πR (3)1°圆心角所对弧长是多少? (4)140°圆心角所对的
弧长是多少?(2)圆的周长可以看作是多少度的圆心角所对的弧?n°ABO若设⊙O半径为R, n°的圆心角所对的弧长为 ,则 探索研究 1例1:已知圆弧的半径为50厘米,圆心角为60°,
求此圆弧的长度。
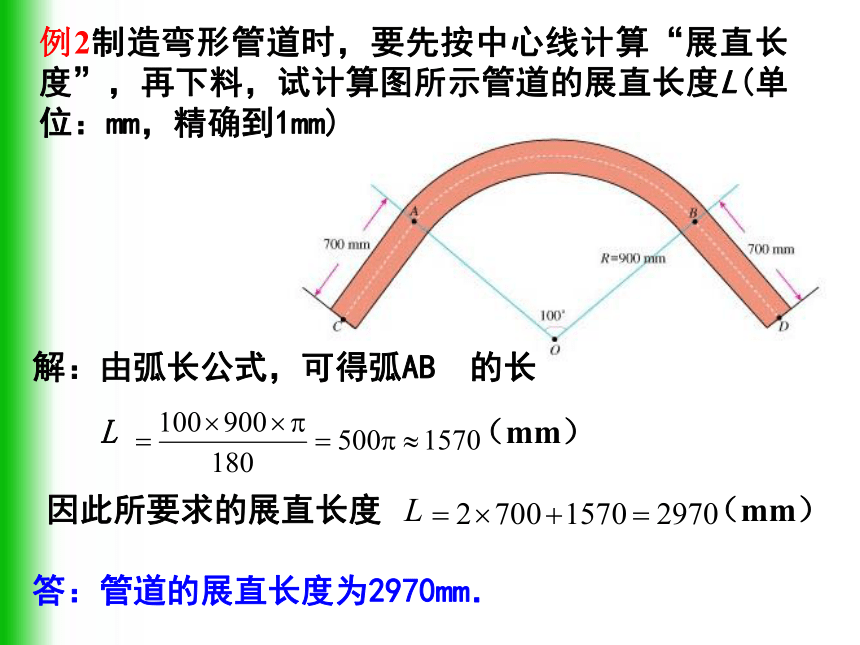
解:例 题 剖 析注意:题目没有特殊要求,最后结果保留到π例2制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
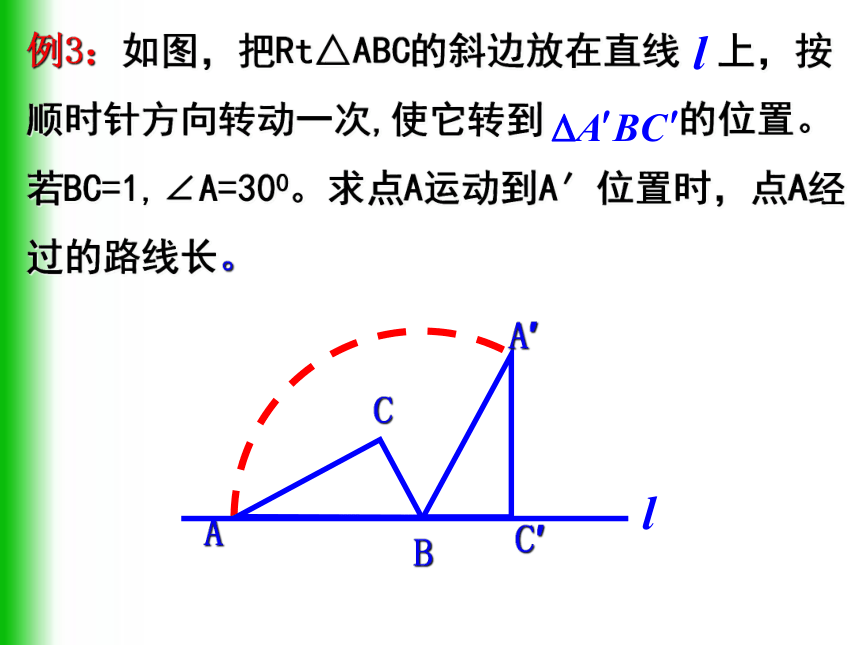
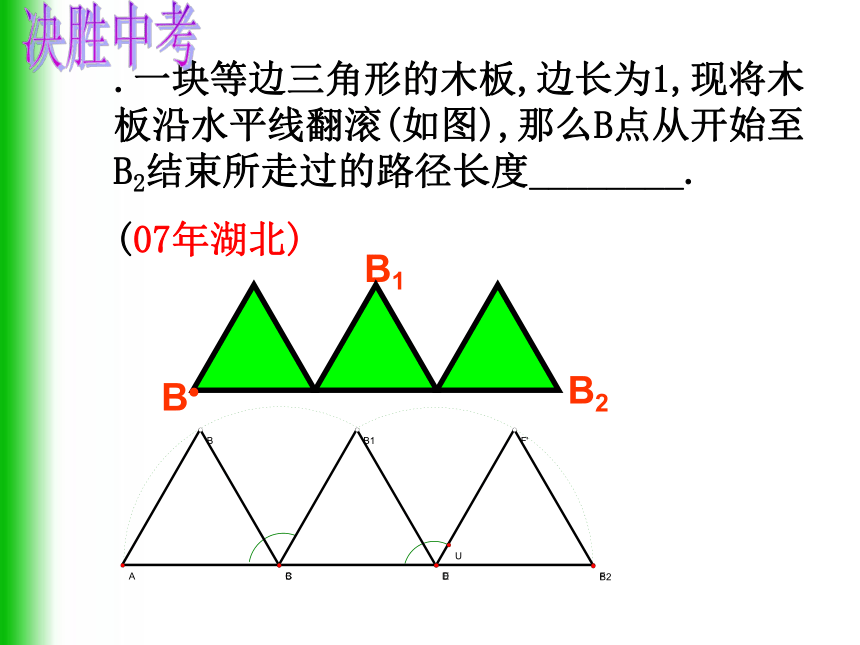
L (mm) 因此所要求的展直长度 L (mm) 答:管道的展直长度为2970mm. 例3:如图,把Rt△ABC的斜边放在直线 上,按顺时针方向转动一次,使它转到 的位置。若BC=1,∠A=300。求点A运动到A′位置时,点A经过的路线长。.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度________.
(07年湖北)BB1B2决胜中考试一试1.已知弧所对的圆心角为900,半径是4,则弧长为______
2. (2006,随州市)已知一条弧的半径为9,弧长为8 ,那么这条弧所对的圆心角为____。
3. (2006,枣庄)钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D. 4、有一段弯道是圆弧形的,道长是12m,弧所对的圆心角是81o,求这段圆弧的半径R(精确到0.1m)(书P122)什 么 是 扇 形 ?扇 形 的 定 义 : 如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。圆心角圆心角AB那么: 在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为探索研究 2 如果圆的半径为R,则圆的面积为 ,
l°的圆心角对应的扇形面积为 ,
°的圆心角对应的扇形面积为 比较扇形面积(S)公式和弧长(l)公式,你能用弧长来表示扇形的面积吗?探索弧长与扇形面积的关系SR感悟点滴想一想:扇形的面积公式与什么公式类似? O比较扇形面积与弧长公式, 用弧长表示扇形面积:1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积,
S扇=____.
2、已知半径为2的扇形,面积为 ,则它的圆心角的度数
为___.
120°练习例4:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)。CD有水部分的面积 = S扇- S△解:如图,连接OA、OB,作弦AB的垂直平分线,垂足为D,交弧AB于点C.
∵OC=0.6,DC=0.3 ∴OD=OC—DC=0.3
在Rt△OAD中,OA=0.6,利用勾股定理可得:AD=0.3√3
在Rt△ OAD中,∵OD=1/2OA
∴∠ OAD=30° ∴∠A OD=60°, ∠ AOB=120°
有水部分的面积DC例5:如图,有一把折扇和一把团扇。已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120 °,问哪一把扇子扇面的面积大?练习:1.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。(结果保留 )ABDCE有水部分的面积
= S扇+ S△3、已知扇形的圆心角为1500,弧长为 ,则扇形的面积为__________.2、已知扇形的圆心角为300,面积为 ,则这个扇形的半径R=____. 1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积为_______.6cm做一做:1:⊙A, ⊙B, ⊙C两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少?弧长的和为多少? (07年北京)决胜中考 2. 如图,⊙A、⊙B、⊙C、⊙D相互外离,它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的面积之和是___________.(07年山东) 3.(2007,山东)如图所示,分别以n边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为 个平方单位. 1. 如图,一根 长的绳子,一端栓在柱子上,另一端栓着一只羊, 羊的活动最大区域面积是 . 生活中的数学3m5m数学乐园ABC数学乐园
制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线的长度),再下料,这就涉及到计算弧长的问题
(1)半径为R的圆,周长是多少?C=2πR (3)1°圆心角所对弧长是多少? (4)140°圆心角所对的
弧长是多少?(2)圆的周长可以看作是多少度的圆心角所对的弧?n°ABO若设⊙O半径为R, n°的圆心角所对的弧长为 ,则 探索研究 1例1:已知圆弧的半径为50厘米,圆心角为60°,
求此圆弧的长度。
解:例 题 剖 析注意:题目没有特殊要求,最后结果保留到π例2制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
L (mm) 因此所要求的展直长度 L (mm) 答:管道的展直长度为2970mm. 例3:如图,把Rt△ABC的斜边放在直线 上,按顺时针方向转动一次,使它转到 的位置。若BC=1,∠A=300。求点A运动到A′位置时,点A经过的路线长。.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度________.
(07年湖北)BB1B2决胜中考试一试1.已知弧所对的圆心角为900,半径是4,则弧长为______
2. (2006,随州市)已知一条弧的半径为9,弧长为8 ,那么这条弧所对的圆心角为____。
3. (2006,枣庄)钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D. 4、有一段弯道是圆弧形的,道长是12m,弧所对的圆心角是81o,求这段圆弧的半径R(精确到0.1m)(书P122)什 么 是 扇 形 ?扇 形 的 定 义 : 如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。圆心角圆心角AB那么: 在半径为R 的圆中,n°的圆心角所对的扇形面积的计算公式为探索研究 2 如果圆的半径为R,则圆的面积为 ,
l°的圆心角对应的扇形面积为 ,
°的圆心角对应的扇形面积为 比较扇形面积(S)公式和弧长(l)公式,你能用弧长来表示扇形的面积吗?探索弧长与扇形面积的关系SR感悟点滴想一想:扇形的面积公式与什么公式类似? O比较扇形面积与弧长公式, 用弧长表示扇形面积:1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积,
S扇=____.
2、已知半径为2的扇形,面积为 ,则它的圆心角的度数
为___.
120°练习例4:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)。CD有水部分的面积 = S扇- S△解:如图,连接OA、OB,作弦AB的垂直平分线,垂足为D,交弧AB于点C.
∵OC=0.6,DC=0.3 ∴OD=OC—DC=0.3
在Rt△OAD中,OA=0.6,利用勾股定理可得:AD=0.3√3
在Rt△ OAD中,∵OD=1/2OA
∴∠ OAD=30° ∴∠A OD=60°, ∠ AOB=120°
有水部分的面积DC例5:如图,有一把折扇和一把团扇。已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120 °,问哪一把扇子扇面的面积大?练习:1.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。(结果保留 )ABDCE有水部分的面积
= S扇+ S△3、已知扇形的圆心角为1500,弧长为 ,则扇形的面积为__________.2、已知扇形的圆心角为300,面积为 ,则这个扇形的半径R=____. 1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积为_______.6cm做一做:1:⊙A, ⊙B, ⊙C两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少?弧长的和为多少? (07年北京)决胜中考 2. 如图,⊙A、⊙B、⊙C、⊙D相互外离,它们的半径都是1,顺次连接四个圆心得到四边形ABCD,则图形中四个扇形(空白部分)的面积之和是___________.(07年山东) 3.(2007,山东)如图所示,分别以n边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为 个平方单位. 1. 如图,一根 长的绳子,一端栓在柱子上,另一端栓着一只羊, 羊的活动最大区域面积是 . 生活中的数学3m5m数学乐园ABC数学乐园
同课章节目录
