矩形复习课(浙江省金华市浦江县)

课件14张PPT。矩 形
菱 形
正方形
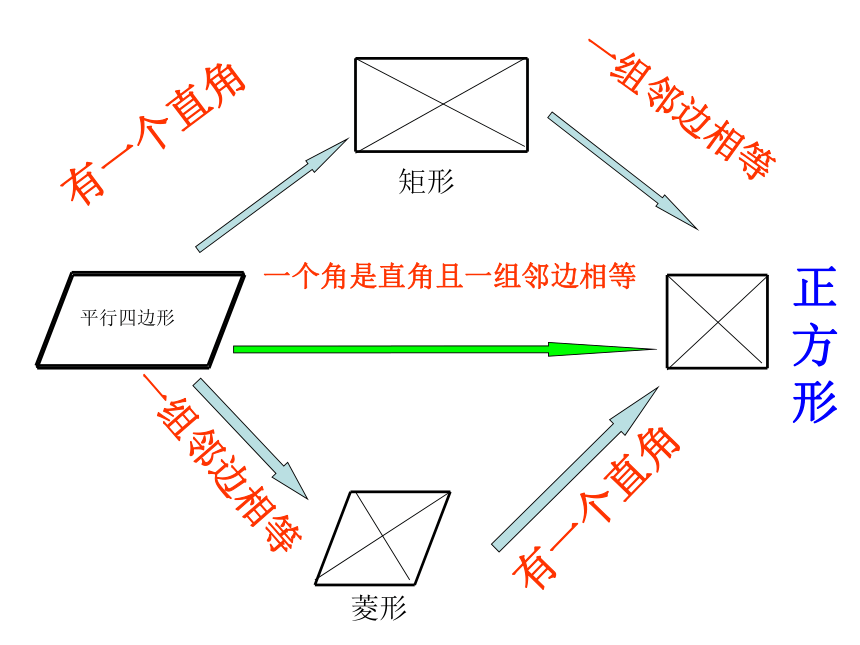
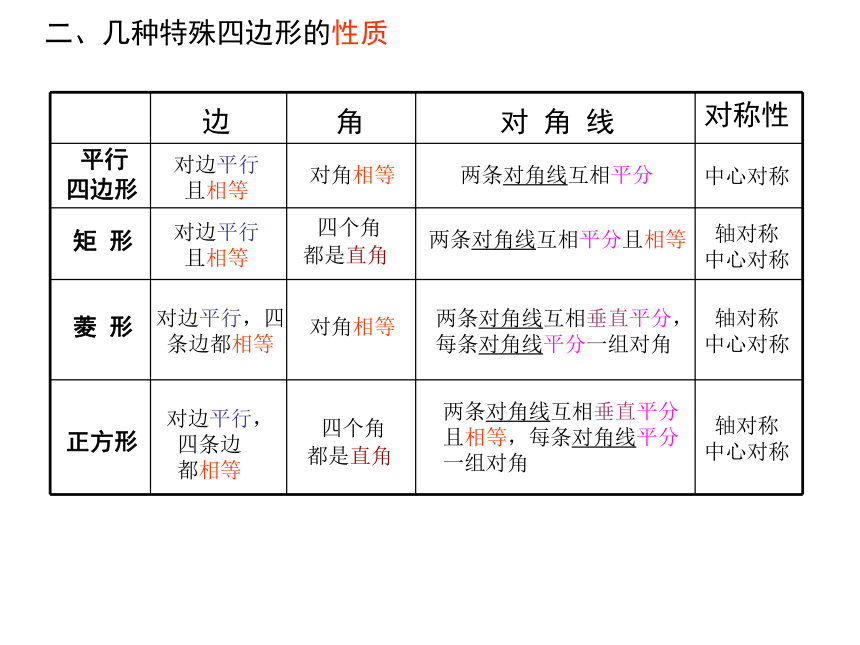
复习课有一个直角一组邻边相等一组邻边相等有一个直角一个角是直角且一组邻边相等正方形平行四边形矩形菱形二、几种特殊四边形的性质 平行
四边形矩 形菱 形正方形边对边平行
且相等对边平行
且相等对边平行，四
条边都相等对边平行，
四条边
都相等角对角相等 四个角
都是直角对角相等 四个角
都是直角对 角 线两条对角线互相平分两条对角线互相平分且相等两条对角线互相垂直平分，
每条对角线平分一组对角两条对角线互相垂直平分
且相等，每条对角线平分
一组对角对称性中心对称 轴对称
中心对称 轴对称
中心对称 轴对称
中心对称三、特殊四边形的常用判定方法 平行
四边形（1）两组对边分别平行；（2）两组对边分别相等；（3）两条对角线互相平分；矩 形（1）有三个角是直角；（2）是平行四边形，并且有一个角是直角；（3）是平行四边形，并且两条对角线相等。 菱 形（1）四条边都相等；（2）是平行四边形，并且有一组邻边相等；（3）是平行四边形，并且两条对角线互相垂直。正方形（1）是矩形，并且有一组邻边相等；（2）是菱形，并且有一个角是直角。典型例题 :例1 :A组题1、矩形、菱形、正方形都具有的性质是（ ）
A、对角线相等 B、对角线互相平分
C、对角线互相垂直 D、四条边都相等 2、已知矩形的一条对角线与另一边的夹角
是40°，则两条对角线所成的锐角的度数是（ ）
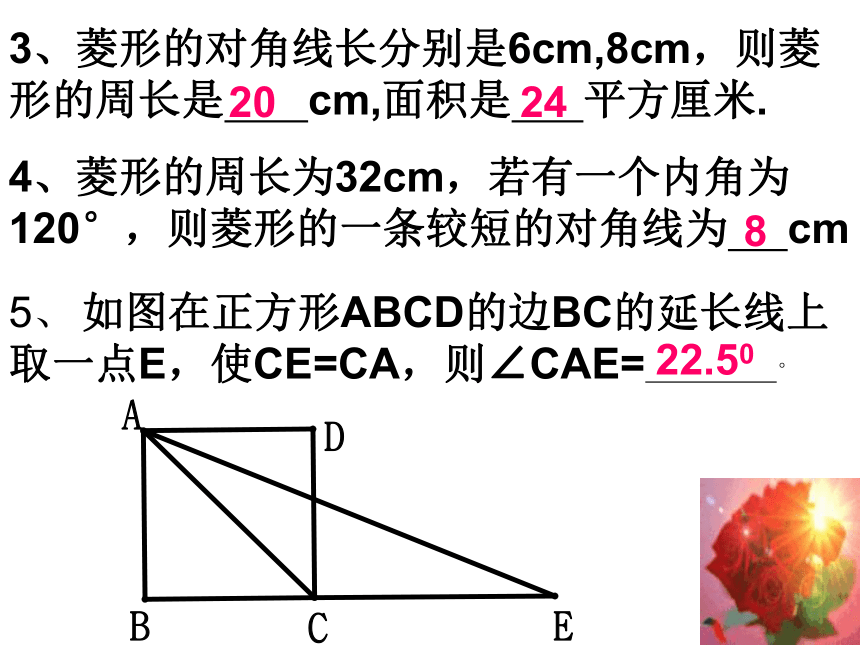
A、50° B、60° C、70° D、80°BD3、菱形的对角线长分别是6cm,8cm，则菱形的周长是 cm,面积是 平方厘米.4、菱形的周长为32cm，若有一个内角为120°，则菱形的一条较短的对角线为 cm 5、 如图在正方形ABCD的边BC的延长线上取一点E，使CE=CA，则∠CAE= ° 2024822.506、正方形ABCD的长为2，E、F分别是AB、BC的中点，则EF的长为 。7、若菱形的两条对角线长是方程
x2－8x＋15＝0的两个根，则该菱形的面积等于________。 8、如图，已知方格纸中是4个相同的正方形，则∠1＋∠2＋∠3＝________。 13507.5B组题例2、如图，矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长和是80cm,对角线是10cm,求矩形的周长。分析：要求矩形的周长，已知中给出了四个三角形的周长，这包括了矩形的四条边和两条对角线长的2倍，所以可用四个三角形的周长减去两条对角线长的2倍即可求得。 例3：如图所示，矩形ABCD的对角线AC、BD相交于点O，AE⊥BD，垂足为E，
∠1＝∠2，OB＝6厘米。 (1)求∠BOC的度数； (2)求△DOC的周长 例4：如图，在菱形ABCD中，CE⊥AB交AB延长线于点E，CF⊥AD交AD延长线于点F，请你猜想CE和CF的大小关系，并证明你的猜想。 例5、如图所示，已知正方形ABCD的对角线AC，BD相交于点O，E是AC上的一点，，过点A作AG⊥EB，垂足是G，AG交BD于F。求证：OE=OF分析：可以把OE、OF分别放在两个三角形△OEB，△OAF中进行证明，条件可由正方形的对角线互相平分且垂直，与已知条件AG⊥EB来创造。拓广：若点E在AC的延长线上，AG⊥EB，AG交EB的延长线于点G，AG的延长线交DB于点F，其他条件不变，OE=OF是否仍然成立？ 若成立，请给出证明；若不成立，请说明理由。例6：根据要求拟编一道新题．C组题已知：如图所示，在矩形ABCD所在平面有一点P，且PA＝PD，请说明：PB＝PC． 请你将上述条件中的“矩形ABCD”改为另一种四边形，其余条件不变，使结论“PB＝PC”仍然成立，再根据改编后的题目画出图形，并说明理由． 例6：把一个等腰直角三角形ABC沿斜边上的高线CD(裁剪线)剪一刀，从这个三角形中裁下一部分，与剩下部分能拼成一个平行四边形A'BCD(如图1)．
以下探究过程中有画图要求的，工具不限，不必写画法和证明． 探究一： (1)想一想——判断四边形A'BCD是平行四边形的依据是__________； (2)做一做——按上述的裁剪方法，请你拼一个与图1位置或形状不同的平行四边形，并在图2中画出示意图． 探究二：在等腰直角三角形ABC中，请你找出其它的剪裁线，把分割成的两部分拼出不同类型的特殊四边形．(1)试一试——你能拼得所有不同类型的特殊四边形有_________，它们的裁剪线分别是_________．(2)画一画——请在图3中画出一个你拼得的特殊四边形示意图。 课外思考： 如图，在四边形ABCD中，AC＝6，BD＝8且AC⊥BD，顺次连结四边形ABCD各边中点，得到四边形A1B1C1D1；再顺次连结四边形A1B1C1D1各边中点，得到四边形A2B2C2D2…如此进行下去得到四边形AnBnCnDn。
(1)证明：四边形A1B1C1D1是矩形；
(2)写出四边形A1B1C1D1和四边形A2B2C2D2的面积；
(3)写出四边形AnBnCnDn的面积；
(4)求四边形A5B5C5D5的周长。