浙教版七年级上册 5.2等式的基本性质 课件(共32张PPT)
文档属性
| 名称 | 浙教版七年级上册 5.2等式的基本性质 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-14 13:50:59 | ||
图片预览











文档简介
(共32张PPT)
知识回顾
1.下面哪些不是一元一次方程?
(1)只含有一个未知数;
(2)经过整理,未知数的最高次数为1次;
(3)含有未知数的代数式必须是整式(整式方程)
三个条件缺一不可
2.下面是方程2x+5=-9的解的是( )
A.x=-2 B.x=2 C.x=7 D.x=-7
代入方程使方程左,右两边相等的未知数的值
②③④
D
5.2 等式的基本性质
学习内容
1 .理解等式的两个性质。
2. 会利用等式的性质解简单的一元一次方程方程。
比较下图中左、右两个天平图,你有什么发现?
一架平衡的天平两边同时加上(或减去)相同质量的砝码,天平仍保持平衡.
新知一:等式的基本性质
新课讲解
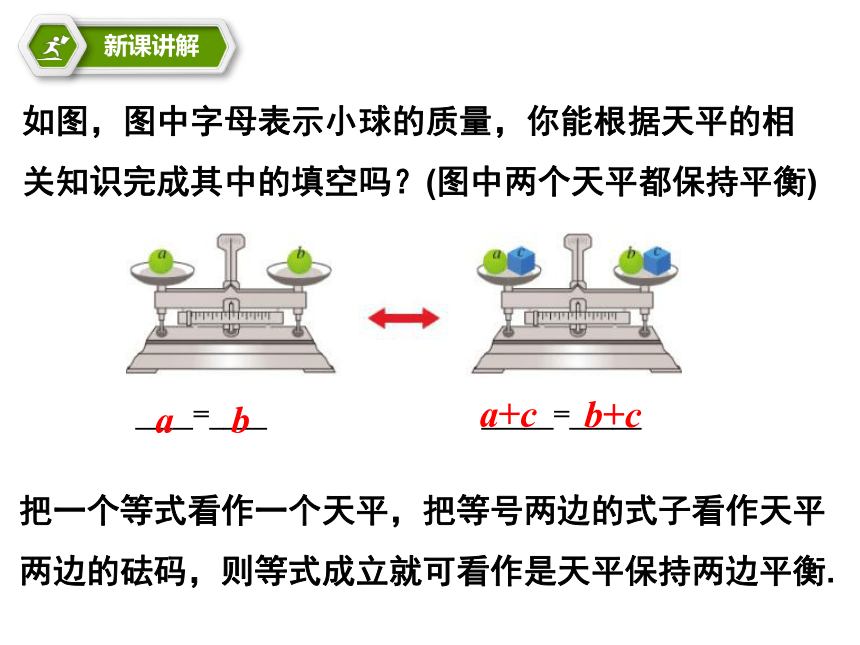
如图,图中字母表示小球的质量,你能根据天平的相关知识完成其中的填空吗?(图中两个天平都保持平衡)
____=____ _____=_____
a
b
a+c
b+c
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.
新课讲解
如果把上面的天平看作是等式,那么等式从左到右发生了怎样的变化?从右到左呢?由此你发现了等式的哪些性质?
把天平看作一个等式,把天平两边的砝码看作等号两边的式子,则天平保持两边平衡就可看作是等式成立.
等式的性质1 等式的两边都加上(或都减去)同一个数或式,所得结果仍是等式.
用字母可表示为:
如果a=b,那么a±c=b±c.
新课讲解
如图,图中字母表示小球的质量,你能根据天平的相关知识完成其中的填空吗?(图中两个天平都保持平衡)
____=____ _____=_____
a
b
3a
3b
新课讲解
如果把上面的天平看作是等式,那么等式从左到右发生了怎样的变化?从右到左呢?由此你又能发现等式的哪些性质?
等式的性质2 等式的两边都乘或都除以同一个数或式(除数不能为零),所得的结果仍是等式.
用字母可表示为:
如果a=b,那么ac=bc,或 .
学以致用
B
3
等式的性质1
-5
等式的性质2
2.已知x+3=1,下列等式成立吗?根据是什么?
(1)3=1-x; (2)-2(x+3)=-2;
(3) ; (4)x=1-3.
解:(1)成立,根据等式的性质1,两边都减去x;
(2)成立,根据等式的性质2,两边都乘以-2;
(3)成立,根据等式的性质2,两边都除以3;
(4)成立,根据等式的性质1,两边都减去3.
3.已知2x-5y=0,且y≠0.判断下列等式是否成立,并说明理由.
(1)2x=5y; (2) .
解:(1)成立.理由如下:
∵2x-5y=0,
∴两边都加上5y,得: 2x-5y+5y=0+5y(等式的性质1)
∴2x=5y.
(2)成立.理由如下:由(1)知2x=5y,而y≠0,
两边都除以2y,得: (等式的性质2).
3.下列方程的变形是否正确?为什么?
(1)由3+x=5,得:x=5+3.
(2)由7x=-4,得:x= .
(3)由 , 得:y=0.
(4)由3=x-2,得:x=-2-3 .
解:(1)由3+x=5,得:x=5+3,变形不正确,
∵方程左边减3,方程的右边加3,
∴变形不正确;
(2)由7x=-4,得x= ,变形正确,
根据等式的性质2,等式两边同除以7;
(3)由 , 得:y=0,变形正确,
根据等式的性质2,等式两边同乘以2;
(4)由3=x-2,得:x=-2-3,变形不正确,
∵左边加x减3,右边减x减3,
∴变形不正确.
学以致用
等式变形需要注意:
1、等式两边都要参加运算,并且是作同一种运算.
2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
3、等式两边不能都除以0,即0不能作除数或分母.
(1)x+2=5 (2)3=x-5
(3)-3x=15
新知二:利用等式的基本性质解方程
例1.利用不等式的性质解下列方程
例1: 解下列方程:
(1)x+2=5
解:方程两边同时减去2,得:
x+2-2=5-2
化简得: x=3
检验方法:
当x=3时,
方程左边=3+2=5,方程右边=5
方程左边=方程右边
∴x=3是方程的解
为什么一定要减去2?
(2)3=x-5
解:方程两边同时加上5,得:
3+5=x-5+5
化简得:
8=x
x=8
注意:习惯上把x写在左边,数字写在右边。
例2 解下列方程:
(1)-3x=15
解:方程两边同时除以-3,得:
化简得:x =-5
代入,检验
为什么一定要除以-3?而不是除以3?
注意:一定要把未知数的项的系数化为1.
除以未知数的项的系数或者乘以它的倒数
注意:解方程就是把方程化简成“x=a”的形式,即把未知数项的系数化为1.
1
注意:(1)方程左边的常数项要去掉;
(2)方程右边的含有未知数的项要去掉.
1.利用等式的性质解下列方程.
(1)3x+1=7; (2)3x+2=x+1.
解:(1)方程得两边都减1,得:3x=6
方程两边都除以3,得:x=2
(2)方程两边都减x,得:2x+2=1,
方程两边都减2,得:2x=-1,
方程得两边都除以2,得: .
学以致用
2 .(1) 由等式3x + 2 = 6 的两边同时________,
得:3x = 4.
(2)由方程 – 2x = 4,两边同时乘以 ,
得:x =-2.
(3)在等式5y – 4 = 6 中,两边同时 ,
可得到5y = 10,再两边同时 ,
得:y = 2。
减去 2
加上 4
除以 5
除以
-2
课堂小结
1.等式的基本性质:
等式的性质1:等式两边同时加上(或减去)同一个代数式,所得结果仍是等式。
等式的性质2:等式两边同时乘以同一个数(或除以同一个不为0的数),所得结果仍是等式。
2.利用等式性质解方程一般方法。
利用等式性质1→ 把方程右边含有的未知数项去掉,方程左边含有的常数项去掉;
利用等式性质2 →把未知数项系数化为1.
3.解方程就是把方程最终化简成“x=a”的形式.
课后巩固
1.(2018—2019·厦门期中)下列等式变形中,错误的是( )
A.由a=b,得a+5=b+5
B.由-3x=-3y,得x=y
C.由x+m=y+m,得x=y
D
B
3.下列变形符合等式性质的是( ).
A.如果2x-3=7,那么2x=7-3
B.如果3x-2=x+1,那么3x-x=1-2
C.如果-2x=5,那么x=5+2
D.如果-x=1,那么x=-1
D
4.已知x=2是关于x的方程3x+a=0的一个解,则a的值是( ).
A.-6 B.-3
C.-4 D.-5
A
5.如果代数式8x-9与6-2x的值互为相反
数,则x的值为 。
6、下列变形符合等式性质的是( )
A、如果2x-3=7,那么2x=7-3
B、如果3x-2=1,那么3x=1-2
C、如果-2x=5,那么x=5+2
D、如果 ,那么x=-3
D
7、依据等式性质进行变形,用得不正确的是( )
A、如果 x+y=5,那么x=5-y
B、如果 x+y=5,那么x+y-5=0
C、如果 x+y=5,那么
D、如果 x+y=5,那么
D
8、填空:
(1)如果 ,那么 =_________.
依据是_________________________________.
(2)如果x-3=5,那么x-3+3=_______,
依据是_________________________________.
(3)如果-3m=12n,那么m=_______,
依据是_________________________________.
(4)如果-0.12x=6,那么x=_______,
依据是_________________________________.
2×0.5
等式的性质2,在等式两边同时乘2
5+3
等式的性质1,在等式两边同加3
-4n
等式的性质2,在等式两边同时除以-3
-50
等式的性质2,在等式两边同除-0.12
教学目标
巩固提升
9、利用等式的性质解下列方程:
(1)x+5=7; (2)-4x=20;
(3)4x-4=8; (4)4x=8x-12.
解:(1)利用等式的性质1,两边都减去5得x+5-5=7-5.即x=2.
(2)利用等式的性质2,两边都除以-4得x= 5.
(3)利用等式的性质1,两边都加上4得4x-4+4=8+4,即4x=12.利用等式的性质2,两边都除以4得x=3.
(4)利用等式的性质1,两边都减去8x得4x-8x=8x-12-8x,即-4x=-12.利用等式的性质2,两边都除以-4得x=3.
21cnjy.com
教学目标
拓展提升
10.要把等式(m-4)x=a化成 ,m必须满足什么条件?
21cnjy.com
解:在(m-4)x=a两边同除以(m-4)
得:
∴m-4≠0
即m≠4
11.小颖碰到一道解方程的题:2x=5x,她在方程的两边都除以x,竟然得到2=5,你能说出她错在哪里吗?
解:能,理由如下:
方程左右两边同都减去5x得:2x-5x=5x-5x
化简得:-3x=0
左右两边都除以-3得:x=0
因此小颖错在她在方程两边同时除以了0.
13.用“●”“■”“▲”分别表示三种不同的物
体,如图所示,前两架天平保持平衡,若要使第三
架天平也平衡,那么“?”处应放“■”的个数为
( )
A.5个 B.4个 C.3个 D.2个
A
设“●”“■”“▲”分别为x、y、z,由图可知,2x=y+z
z=x+y,解得x=2y,z=3y,
所以x+z=2y+3y=5y,即“■”的个数为5,
故选A.
谢 谢!
知识回顾
1.下面哪些不是一元一次方程?
(1)只含有一个未知数;
(2)经过整理,未知数的最高次数为1次;
(3)含有未知数的代数式必须是整式(整式方程)
三个条件缺一不可
2.下面是方程2x+5=-9的解的是( )
A.x=-2 B.x=2 C.x=7 D.x=-7
代入方程使方程左,右两边相等的未知数的值
②③④
D
5.2 等式的基本性质
学习内容
1 .理解等式的两个性质。
2. 会利用等式的性质解简单的一元一次方程方程。
比较下图中左、右两个天平图,你有什么发现?
一架平衡的天平两边同时加上(或减去)相同质量的砝码,天平仍保持平衡.
新知一:等式的基本性质
新课讲解
如图,图中字母表示小球的质量,你能根据天平的相关知识完成其中的填空吗?(图中两个天平都保持平衡)
____=____ _____=_____
a
b
a+c
b+c
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.
新课讲解
如果把上面的天平看作是等式,那么等式从左到右发生了怎样的变化?从右到左呢?由此你发现了等式的哪些性质?
把天平看作一个等式,把天平两边的砝码看作等号两边的式子,则天平保持两边平衡就可看作是等式成立.
等式的性质1 等式的两边都加上(或都减去)同一个数或式,所得结果仍是等式.
用字母可表示为:
如果a=b,那么a±c=b±c.
新课讲解
如图,图中字母表示小球的质量,你能根据天平的相关知识完成其中的填空吗?(图中两个天平都保持平衡)
____=____ _____=_____
a
b
3a
3b
新课讲解
如果把上面的天平看作是等式,那么等式从左到右发生了怎样的变化?从右到左呢?由此你又能发现等式的哪些性质?
等式的性质2 等式的两边都乘或都除以同一个数或式(除数不能为零),所得的结果仍是等式.
用字母可表示为:
如果a=b,那么ac=bc,或 .
学以致用
B
3
等式的性质1
-5
等式的性质2
2.已知x+3=1,下列等式成立吗?根据是什么?
(1)3=1-x; (2)-2(x+3)=-2;
(3) ; (4)x=1-3.
解:(1)成立,根据等式的性质1,两边都减去x;
(2)成立,根据等式的性质2,两边都乘以-2;
(3)成立,根据等式的性质2,两边都除以3;
(4)成立,根据等式的性质1,两边都减去3.
3.已知2x-5y=0,且y≠0.判断下列等式是否成立,并说明理由.
(1)2x=5y; (2) .
解:(1)成立.理由如下:
∵2x-5y=0,
∴两边都加上5y,得: 2x-5y+5y=0+5y(等式的性质1)
∴2x=5y.
(2)成立.理由如下:由(1)知2x=5y,而y≠0,
两边都除以2y,得: (等式的性质2).
3.下列方程的变形是否正确?为什么?
(1)由3+x=5,得:x=5+3.
(2)由7x=-4,得:x= .
(3)由 , 得:y=0.
(4)由3=x-2,得:x=-2-3 .
解:(1)由3+x=5,得:x=5+3,变形不正确,
∵方程左边减3,方程的右边加3,
∴变形不正确;
(2)由7x=-4,得x= ,变形正确,
根据等式的性质2,等式两边同除以7;
(3)由 , 得:y=0,变形正确,
根据等式的性质2,等式两边同乘以2;
(4)由3=x-2,得:x=-2-3,变形不正确,
∵左边加x减3,右边减x减3,
∴变形不正确.
学以致用
等式变形需要注意:
1、等式两边都要参加运算,并且是作同一种运算.
2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
3、等式两边不能都除以0,即0不能作除数或分母.
(1)x+2=5 (2)3=x-5
(3)-3x=15
新知二:利用等式的基本性质解方程
例1.利用不等式的性质解下列方程
例1: 解下列方程:
(1)x+2=5
解:方程两边同时减去2,得:
x+2-2=5-2
化简得: x=3
检验方法:
当x=3时,
方程左边=3+2=5,方程右边=5
方程左边=方程右边
∴x=3是方程的解
为什么一定要减去2?
(2)3=x-5
解:方程两边同时加上5,得:
3+5=x-5+5
化简得:
8=x
x=8
注意:习惯上把x写在左边,数字写在右边。
例2 解下列方程:
(1)-3x=15
解:方程两边同时除以-3,得:
化简得:x =-5
代入,检验
为什么一定要除以-3?而不是除以3?
注意:一定要把未知数的项的系数化为1.
除以未知数的项的系数或者乘以它的倒数
注意:解方程就是把方程化简成“x=a”的形式,即把未知数项的系数化为1.
1
注意:(1)方程左边的常数项要去掉;
(2)方程右边的含有未知数的项要去掉.
1.利用等式的性质解下列方程.
(1)3x+1=7; (2)3x+2=x+1.
解:(1)方程得两边都减1,得:3x=6
方程两边都除以3,得:x=2
(2)方程两边都减x,得:2x+2=1,
方程两边都减2,得:2x=-1,
方程得两边都除以2,得: .
学以致用
2 .(1) 由等式3x + 2 = 6 的两边同时________,
得:3x = 4.
(2)由方程 – 2x = 4,两边同时乘以 ,
得:x =-2.
(3)在等式5y – 4 = 6 中,两边同时 ,
可得到5y = 10,再两边同时 ,
得:y = 2。
减去 2
加上 4
除以 5
除以
-2
课堂小结
1.等式的基本性质:
等式的性质1:等式两边同时加上(或减去)同一个代数式,所得结果仍是等式。
等式的性质2:等式两边同时乘以同一个数(或除以同一个不为0的数),所得结果仍是等式。
2.利用等式性质解方程一般方法。
利用等式性质1→ 把方程右边含有的未知数项去掉,方程左边含有的常数项去掉;
利用等式性质2 →把未知数项系数化为1.
3.解方程就是把方程最终化简成“x=a”的形式.
课后巩固
1.(2018—2019·厦门期中)下列等式变形中,错误的是( )
A.由a=b,得a+5=b+5
B.由-3x=-3y,得x=y
C.由x+m=y+m,得x=y
D
B
3.下列变形符合等式性质的是( ).
A.如果2x-3=7,那么2x=7-3
B.如果3x-2=x+1,那么3x-x=1-2
C.如果-2x=5,那么x=5+2
D.如果-x=1,那么x=-1
D
4.已知x=2是关于x的方程3x+a=0的一个解,则a的值是( ).
A.-6 B.-3
C.-4 D.-5
A
5.如果代数式8x-9与6-2x的值互为相反
数,则x的值为 。
6、下列变形符合等式性质的是( )
A、如果2x-3=7,那么2x=7-3
B、如果3x-2=1,那么3x=1-2
C、如果-2x=5,那么x=5+2
D、如果 ,那么x=-3
D
7、依据等式性质进行变形,用得不正确的是( )
A、如果 x+y=5,那么x=5-y
B、如果 x+y=5,那么x+y-5=0
C、如果 x+y=5,那么
D、如果 x+y=5,那么
D
8、填空:
(1)如果 ,那么 =_________.
依据是_________________________________.
(2)如果x-3=5,那么x-3+3=_______,
依据是_________________________________.
(3)如果-3m=12n,那么m=_______,
依据是_________________________________.
(4)如果-0.12x=6,那么x=_______,
依据是_________________________________.
2×0.5
等式的性质2,在等式两边同时乘2
5+3
等式的性质1,在等式两边同加3
-4n
等式的性质2,在等式两边同时除以-3
-50
等式的性质2,在等式两边同除-0.12
教学目标
巩固提升
9、利用等式的性质解下列方程:
(1)x+5=7; (2)-4x=20;
(3)4x-4=8; (4)4x=8x-12.
解:(1)利用等式的性质1,两边都减去5得x+5-5=7-5.即x=2.
(2)利用等式的性质2,两边都除以-4得x= 5.
(3)利用等式的性质1,两边都加上4得4x-4+4=8+4,即4x=12.利用等式的性质2,两边都除以4得x=3.
(4)利用等式的性质1,两边都减去8x得4x-8x=8x-12-8x,即-4x=-12.利用等式的性质2,两边都除以-4得x=3.
21cnjy.com
教学目标
拓展提升
10.要把等式(m-4)x=a化成 ,m必须满足什么条件?
21cnjy.com
解:在(m-4)x=a两边同除以(m-4)
得:
∴m-4≠0
即m≠4
11.小颖碰到一道解方程的题:2x=5x,她在方程的两边都除以x,竟然得到2=5,你能说出她错在哪里吗?
解:能,理由如下:
方程左右两边同都减去5x得:2x-5x=5x-5x
化简得:-3x=0
左右两边都除以-3得:x=0
因此小颖错在她在方程两边同时除以了0.
13.用“●”“■”“▲”分别表示三种不同的物
体,如图所示,前两架天平保持平衡,若要使第三
架天平也平衡,那么“?”处应放“■”的个数为
( )
A.5个 B.4个 C.3个 D.2个
A
设“●”“■”“▲”分别为x、y、z,由图可知,2x=y+z
z=x+y,解得x=2y,z=3y,
所以x+z=2y+3y=5y,即“■”的个数为5,
故选A.
谢 谢!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
