浙教版八年级数学上册2.3 等腰三角形的性质定理 同步练习(无答案)
文档属性
| 名称 | 浙教版八年级数学上册2.3 等腰三角形的性质定理 同步练习(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 148.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-15 11:23:19 | ||
图片预览


文档简介
浙教版八年级上册2.3 等腰三角形的性质定理
一、选择题
1. 下列命题中真命题是( )
A.三角形按边可分为不等边三角形,等腰三角形和等边三角形
B.等边三角形有条对称轴,它们是三条边上的高
C.三角形的一个外角大于任何一个内角
D.三角形三条内角平分线相交于一点,这点到三角形三边的距离相等
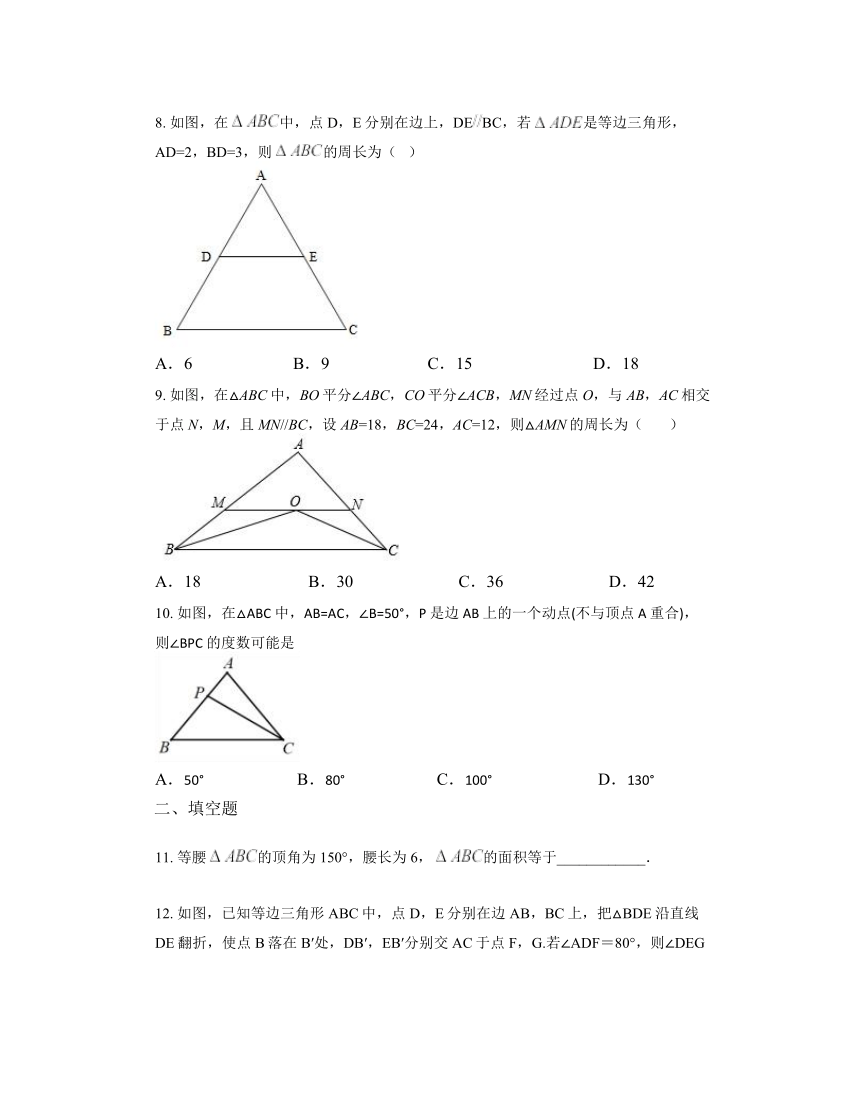
2. 如图,等边三角形ABC中,AD⊥BC于D,BE平分∠ABC交AD、AC于点O、E, ABC的重心是( )
A.点D B.点E C.点O D.不能确定
3. 如图,将一块等边三角形纸板与直尺叠放在一起,且等边三角形纸板的一个顶点在直尺的一边上,则与的数量关系为( )
A. B. C. D.
4. 如图,直线,是等边三角形,,则的大小为( )
A. B. C. D.
5. 在中,,的中垂线交,于点,,的周长是8,,则的周长是( )
A.10 B.11 C.12 D.13
6. 如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
7. 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
A.7.5 B.5 C.4 D.不能确定
8. 如图,在中,点D,E分别在边上,DEBC,若是等边三角形,AD=2,BD=3,则的周长为( )
A.6 B.9 C.15 D.18
9. 如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O,与AB,AC相交于点N,M,且MN//BC,设AB=18,BC=24,AC=12,则△AMN的周长为( )
A.18 B.30 C.36 D.42
10. 如图,在△ABC 中,AB=AC,∠B=50°,P 是边 AB 上的一个动点(不与顶点 A 重合),则∠BPC 的度数可能是
A.50° B.80° C.100° D.130°
二、填空题
11. 等腰的顶角为150°,腰长为6,的面积等于____________.
12. 如图,已知等边三角形ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交AC于点F,G.若∠ADF=80°,则∠DEG的度数为________.
13. 已知等腰三角形的一边长等于3,一边长等于7,则它的周长为 _______.
14. 在△ABC中,∠A=36°.当∠C=______________°,△ABC为等腰三角形.
三、解答题
15. 如图,中,,点M、N分别从点A、点B同时出发,沿三角形的边顺时针运动,点M的速度为2cm/s,点N的速度为3cm/s,当点M,点N第一次相遇时,点M,点N同时停止运动.设点M,点N的运动时间为秒.
(1)当点M在上时, ;当点M在上时, .(用含的代数式表示)
(2)点N在上时,若为直角三角形,直接写出的值.
(3)连结,当线段的垂直平分线经的某一顶点时,直接写出的值.
16. 综合与实践
问题情境
如图1,和均为等边三角形,点,,在同一条直线上,连接;
探究发现
(1)善思组发现:,请你帮他们写出推理过程;
(2)钻研组受善思组的启发,求出了度数,请直接写出等于______度;
(3)奋进组在前面两组的基础上又探索出了与的位置关系为______(请直接写出结果);
拓展探究
(4)如图2,和均为等腰直角三角形,,点,,在同一条直线上,为中边上的高,连接,试探究,,之间有怎样的数量关系.
创新组类比善思组的发现,很快证出,进而得出.请你写出,,之间的数量关系并帮创新组完成后续的证明过程.
17. 【发现问题】小强在一次学习过程中遇到了下面的问题:如图①,是的中线,若,求的取值范围.
【探究方法】小强所在的小组通过探究发现,延长至点E,使.连接,可以证出,利用全等三角形的性质可将已知的边长与转化到到中,进而求出的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法”.
(1)请你利用上面解答问题的思路方法,写出求的取值范围的过程;
(2)【问题解决】如图②,是的中线,是的中线,且,下列四个选项中:
A. B. C. D.
直接写出所有正确选项的序号是 .
(3)【问题拓展】如图③,在和中, ,与互补,连接、,E是的中点,求证:.
18. 已知是边长为4的等边三角形,点是射线上的动点,将线段绕点顺时针方向旋转得到线段,连接.
(1)如图1,求证:;
(2)①当________时,;(直接写出结果)
②点在运动过程中,的周长是否存在最小值?若存在.请直接写出周长的最小值;若不存在,请说明理由.
一、选择题
1. 下列命题中真命题是( )
A.三角形按边可分为不等边三角形,等腰三角形和等边三角形
B.等边三角形有条对称轴,它们是三条边上的高
C.三角形的一个外角大于任何一个内角
D.三角形三条内角平分线相交于一点,这点到三角形三边的距离相等
2. 如图,等边三角形ABC中,AD⊥BC于D,BE平分∠ABC交AD、AC于点O、E, ABC的重心是( )
A.点D B.点E C.点O D.不能确定
3. 如图,将一块等边三角形纸板与直尺叠放在一起,且等边三角形纸板的一个顶点在直尺的一边上,则与的数量关系为( )
A. B. C. D.
4. 如图,直线,是等边三角形,,则的大小为( )
A. B. C. D.
5. 在中,,的中垂线交,于点,,的周长是8,,则的周长是( )
A.10 B.11 C.12 D.13
6. 如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
7. 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
A.7.5 B.5 C.4 D.不能确定
8. 如图,在中,点D,E分别在边上,DEBC,若是等边三角形,AD=2,BD=3,则的周长为( )
A.6 B.9 C.15 D.18
9. 如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O,与AB,AC相交于点N,M,且MN//BC,设AB=18,BC=24,AC=12,则△AMN的周长为( )
A.18 B.30 C.36 D.42
10. 如图,在△ABC 中,AB=AC,∠B=50°,P 是边 AB 上的一个动点(不与顶点 A 重合),则∠BPC 的度数可能是
A.50° B.80° C.100° D.130°
二、填空题
11. 等腰的顶角为150°,腰长为6,的面积等于____________.
12. 如图,已知等边三角形ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在B′处,DB′,EB′分别交AC于点F,G.若∠ADF=80°,则∠DEG的度数为________.
13. 已知等腰三角形的一边长等于3,一边长等于7,则它的周长为 _______.
14. 在△ABC中,∠A=36°.当∠C=______________°,△ABC为等腰三角形.
三、解答题
15. 如图,中,,点M、N分别从点A、点B同时出发,沿三角形的边顺时针运动,点M的速度为2cm/s,点N的速度为3cm/s,当点M,点N第一次相遇时,点M,点N同时停止运动.设点M,点N的运动时间为秒.
(1)当点M在上时, ;当点M在上时, .(用含的代数式表示)
(2)点N在上时,若为直角三角形,直接写出的值.
(3)连结,当线段的垂直平分线经的某一顶点时,直接写出的值.
16. 综合与实践
问题情境
如图1,和均为等边三角形,点,,在同一条直线上,连接;
探究发现
(1)善思组发现:,请你帮他们写出推理过程;
(2)钻研组受善思组的启发,求出了度数,请直接写出等于______度;
(3)奋进组在前面两组的基础上又探索出了与的位置关系为______(请直接写出结果);
拓展探究
(4)如图2,和均为等腰直角三角形,,点,,在同一条直线上,为中边上的高,连接,试探究,,之间有怎样的数量关系.
创新组类比善思组的发现,很快证出,进而得出.请你写出,,之间的数量关系并帮创新组完成后续的证明过程.
17. 【发现问题】小强在一次学习过程中遇到了下面的问题:如图①,是的中线,若,求的取值范围.
【探究方法】小强所在的小组通过探究发现,延长至点E,使.连接,可以证出,利用全等三角形的性质可将已知的边长与转化到到中,进而求出的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法”.
(1)请你利用上面解答问题的思路方法,写出求的取值范围的过程;
(2)【问题解决】如图②,是的中线,是的中线,且,下列四个选项中:
A. B. C. D.
直接写出所有正确选项的序号是 .
(3)【问题拓展】如图③,在和中, ,与互补,连接、,E是的中点,求证:.
18. 已知是边长为4的等边三角形,点是射线上的动点,将线段绕点顺时针方向旋转得到线段,连接.
(1)如图1,求证:;
(2)①当________时,;(直接写出结果)
②点在运动过程中,的周长是否存在最小值?若存在.请直接写出周长的最小值;若不存在,请说明理由.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
