4.4相似三角形的性质及应用(2)(浙江省宁波市)
文档属性
| 名称 | 4.4相似三角形的性质及应用(2)(浙江省宁波市) |
|
|
| 格式 | rar | ||
| 文件大小 | 505.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-16 00:00:00 | ||
图片预览


文档简介
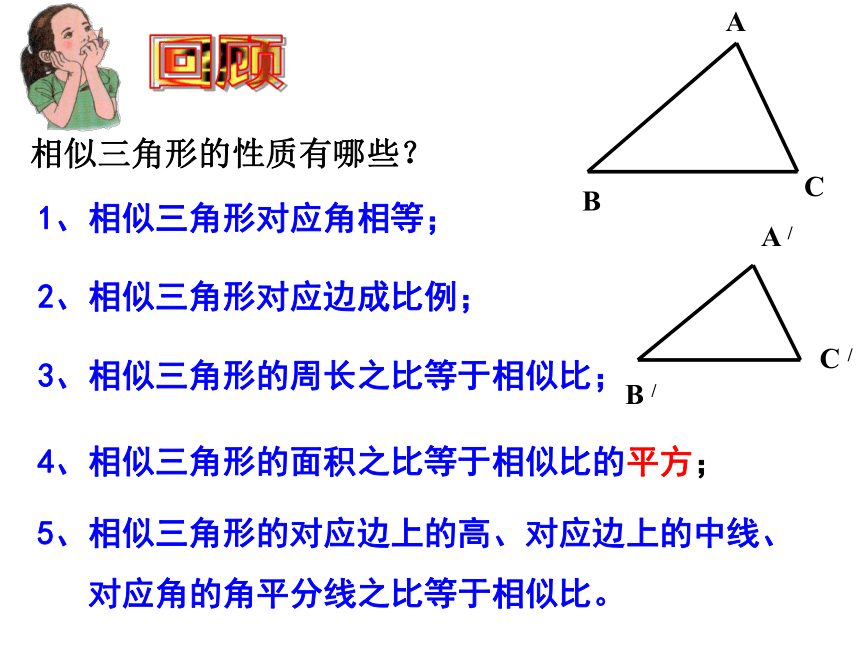
课件17张PPT。4.4相似三角形的性质及其应用(2)浙教版九年级《数学》上册相似三角形的性质有哪些?1、相似三角形对应角相等;2、相似三角形对应边成比例; 3、相似三角形的周长之比等于相似比;4、相似三角形的面积之比等于相似比的平方;5、相似三角形的对应边上的高、对应边上的中线、
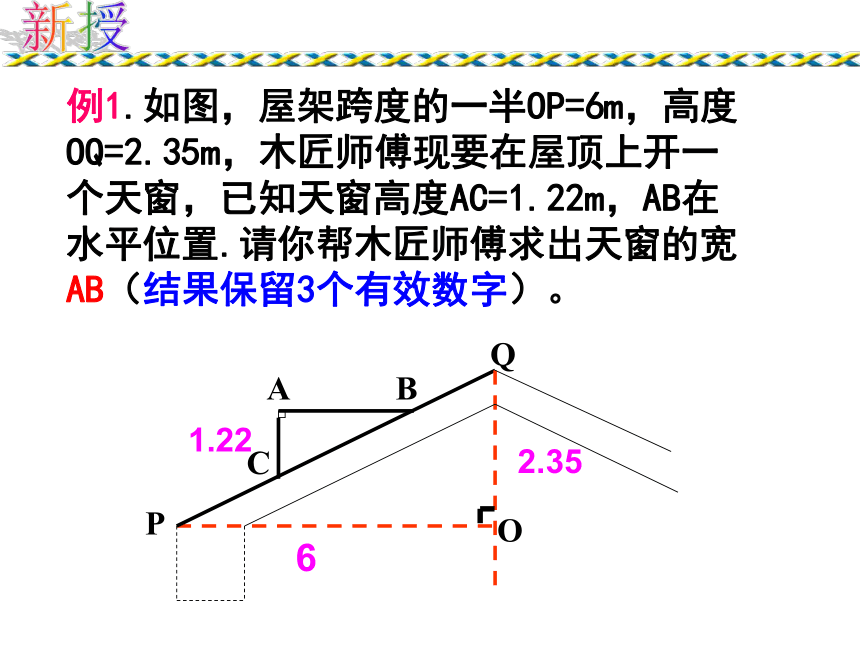
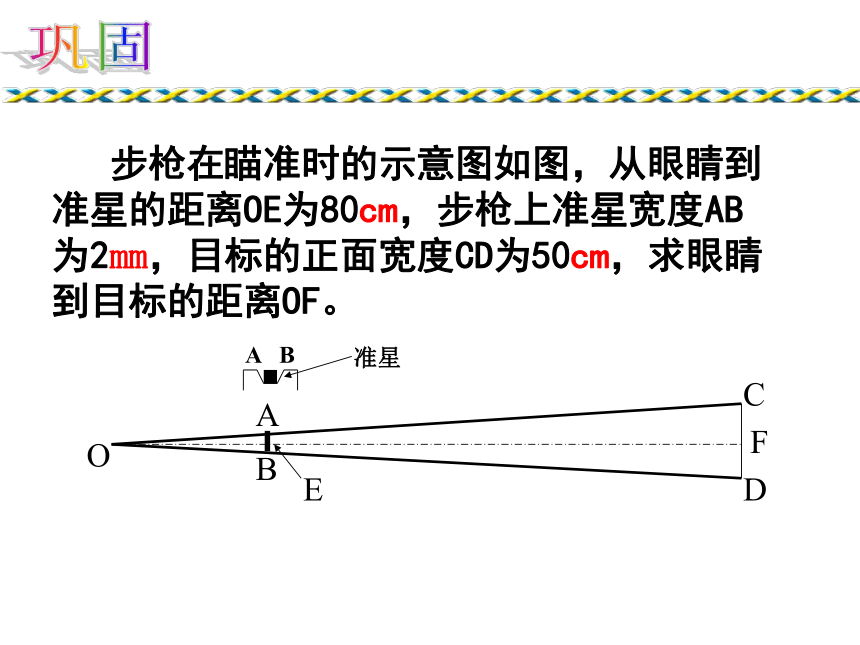
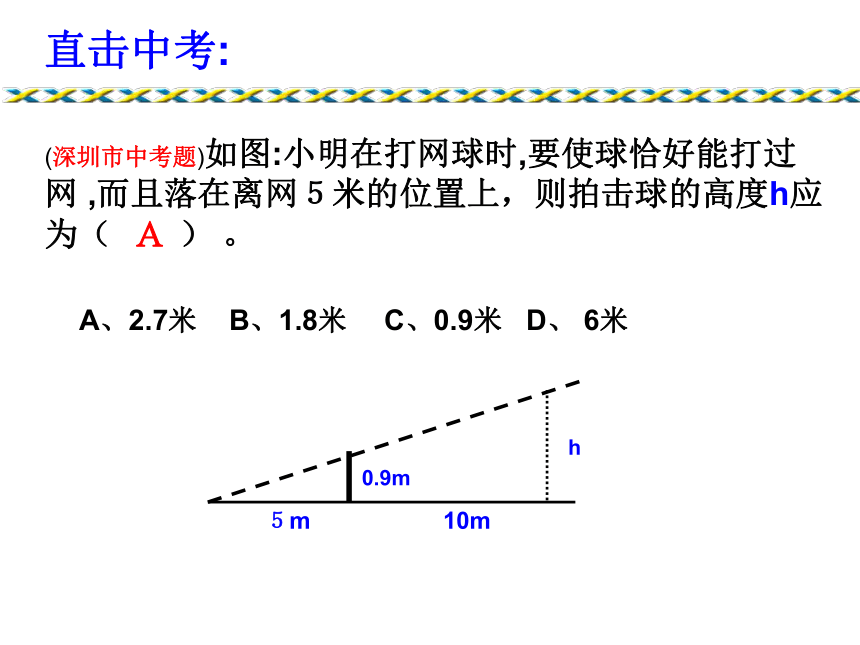
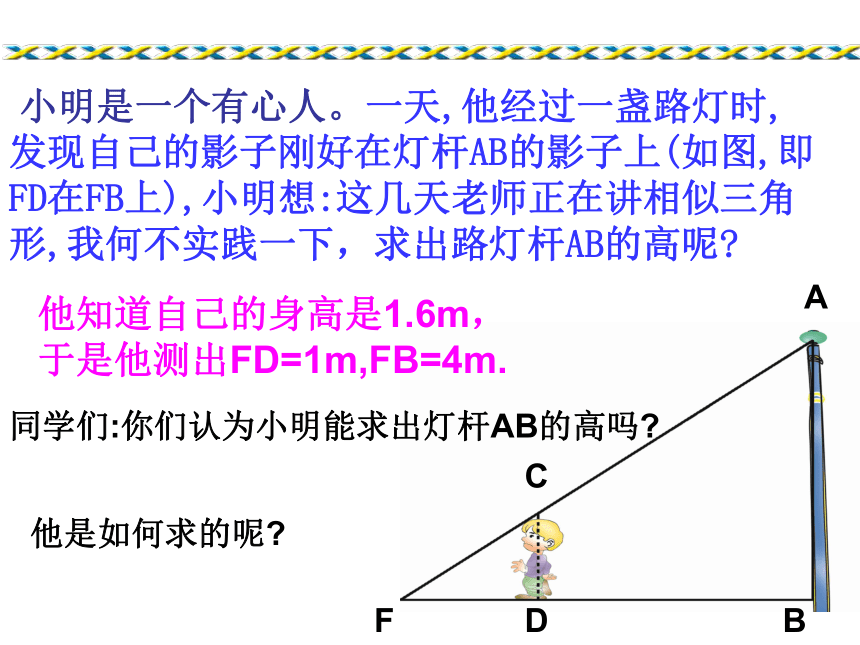
对应角的角平分线之比等于相似比。回顾例1.如图,屋架跨度的一半OP=6m,高度OQ=2.35m,木匠师傅现要在屋顶上开一个天窗,已知天窗高度AC=1.22m,AB在水平位置.请你帮木匠师傅求出天窗的宽AB(结果保留3个有效数字)。新授62.351.22 步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,求眼睛到目标的距离OF。巩固直击中考:(深圳市中考题)如图:小明在打网球时,要使球恰好能打过网 ,而且落在离网5米的位置上,则拍击球的高度h应为( ) 。A、2.7米 B、1.8米 C、0.9米 D、 6米 A 小明是一个有心人。一天,他经过一盏路灯时,发现自己的影子刚好在灯杆AB的影子上(如图,即FD在FB上),小明想:这几天老师正在讲相似三角形,我何不实践一下,求出路灯杆AB的高呢?ABDFC他知道自己的身高是1.6m,于是他测出FD=1m,FB=4m.同学们:你们认为小明能求出灯杆AB的高吗?他是如何求的呢?例2:
小明不仅是个有心人,还是个爱动脑筋的孩子 .在一次户外游玩中,他发现一棵“很高很高”的白杨树,他特别想知道“这棵白杨树到底有多高”.于是他从附近的店里借来皮尺(足够长)、标杆(2.80米)、镜子等工具,他只选了其中的部分工具,就设计出了测量白杨树高的方案,并求出了此树的高度。同学们,你们知道小明的方案是如何设计的吗?他是如何求出树高的? 方案1:小明把长为2.80m的标杆CD直立在地面上,如果量出树的影长为9.62m,标杆的影长为1.27m,这时树高多少?你能解决这个问题吗? (精确到0.1m) ABCDEF2.809.621.27
小明把一小镜子放在离树(AB)16米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=1.21m,观察者目高CD=1.6m,这时树高多少?你能解决这个问题吗? (精确到0.1m) ABEDC方案2:课外思考方案161.211.6 小明不仅爱动脑筋,而且还是个乐于助人的孩子。一次同学小刚拿来一题请教小明:如图,零件的外径为a,要求它的厚度x。现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=3,且量得CD=b,求厚度x。小明思索了一会儿,马上给小刚讲解起来。你知道他是如何分析并解答的吗?O(分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB。而在图中可构造出相似三角形,通过相似三角形的性质,从而求出AB的长度。)O一 、相似三角形的应用主要体现在哪些方面?二、解决方法三、解决步骤一般步骤:①审题 ②找相似或构造相似三角形
③利用相似三角形解决问题谈谈你的收获课堂小结常找相似三角形或构造相似三角形求解1、求线段长度2、测物体高度(用皮尺等工具无法直接测得的高)2.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m。 1m16m0.5m8?1.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为 . 反馈4米挑战自我如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,问加工成的正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN的边长为x毫米。即答:这个正方形的 边长是48毫米。∴ ∴△APN∽ △ABC∵PN∥BC,∴ x=48(毫米)。1、独立作业:见作业本(1)2、合作作业:
进一步思考测量树高的方案.结束寄语不经历风雨,怎么见彩虹,没有人能随随便便成功!希望同学们做一个生活的有心人,
勤于思考,乐于助人!谢谢指导!
对应角的角平分线之比等于相似比。回顾例1.如图,屋架跨度的一半OP=6m,高度OQ=2.35m,木匠师傅现要在屋顶上开一个天窗,已知天窗高度AC=1.22m,AB在水平位置.请你帮木匠师傅求出天窗的宽AB(结果保留3个有效数字)。新授62.351.22 步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,求眼睛到目标的距离OF。巩固直击中考:(深圳市中考题)如图:小明在打网球时,要使球恰好能打过网 ,而且落在离网5米的位置上,则拍击球的高度h应为( ) 。A、2.7米 B、1.8米 C、0.9米 D、 6米 A 小明是一个有心人。一天,他经过一盏路灯时,发现自己的影子刚好在灯杆AB的影子上(如图,即FD在FB上),小明想:这几天老师正在讲相似三角形,我何不实践一下,求出路灯杆AB的高呢?ABDFC他知道自己的身高是1.6m,于是他测出FD=1m,FB=4m.同学们:你们认为小明能求出灯杆AB的高吗?他是如何求的呢?例2:
小明不仅是个有心人,还是个爱动脑筋的孩子 .在一次户外游玩中,他发现一棵“很高很高”的白杨树,他特别想知道“这棵白杨树到底有多高”.于是他从附近的店里借来皮尺(足够长)、标杆(2.80米)、镜子等工具,他只选了其中的部分工具,就设计出了测量白杨树高的方案,并求出了此树的高度。同学们,你们知道小明的方案是如何设计的吗?他是如何求出树高的? 方案1:小明把长为2.80m的标杆CD直立在地面上,如果量出树的影长为9.62m,标杆的影长为1.27m,这时树高多少?你能解决这个问题吗? (精确到0.1m) ABCDEF2.809.621.27
小明把一小镜子放在离树(AB)16米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=1.21m,观察者目高CD=1.6m,这时树高多少?你能解决这个问题吗? (精确到0.1m) ABEDC方案2:课外思考方案161.211.6 小明不仅爱动脑筋,而且还是个乐于助人的孩子。一次同学小刚拿来一题请教小明:如图,零件的外径为a,要求它的厚度x。现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=3,且量得CD=b,求厚度x。小明思索了一会儿,马上给小刚讲解起来。你知道他是如何分析并解答的吗?O(分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB。而在图中可构造出相似三角形,通过相似三角形的性质,从而求出AB的长度。)O一 、相似三角形的应用主要体现在哪些方面?二、解决方法三、解决步骤一般步骤:①审题 ②找相似或构造相似三角形
③利用相似三角形解决问题谈谈你的收获课堂小结常找相似三角形或构造相似三角形求解1、求线段长度2、测物体高度(用皮尺等工具无法直接测得的高)2.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m。 1m16m0.5m8?1.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为 . 反馈4米挑战自我如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,问加工成的正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN的边长为x毫米。即答:这个正方形的 边长是48毫米。∴ ∴△APN∽ △ABC∵PN∥BC,∴ x=48(毫米)。1、独立作业:见作业本(1)2、合作作业:
进一步思考测量树高的方案.结束寄语不经历风雨,怎么见彩虹,没有人能随随便便成功!希望同学们做一个生活的有心人,
勤于思考,乐于助人!谢谢指导!
同课章节目录
