浙教版数学八年级上册《5.5一次函数的简单应用(1)》课件(共15张PPT)
文档属性
| 名称 | 浙教版数学八年级上册《5.5一次函数的简单应用(1)》课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 15:04:37 | ||
图片预览




文档简介
(共15张PPT)
5.5 一次函数的简单应用(1)
第5章 一次函数
浙教版 八年级上册
学习目标
学习目标
(1)了解通过实验获得数据,然后根据数据建立一次函数模型的一般过程.
(2)会综合运用一次函数的表达式,函数图象以及结合方程(组)等其他数学模型,解决实际问题.
课前复习
课前复习
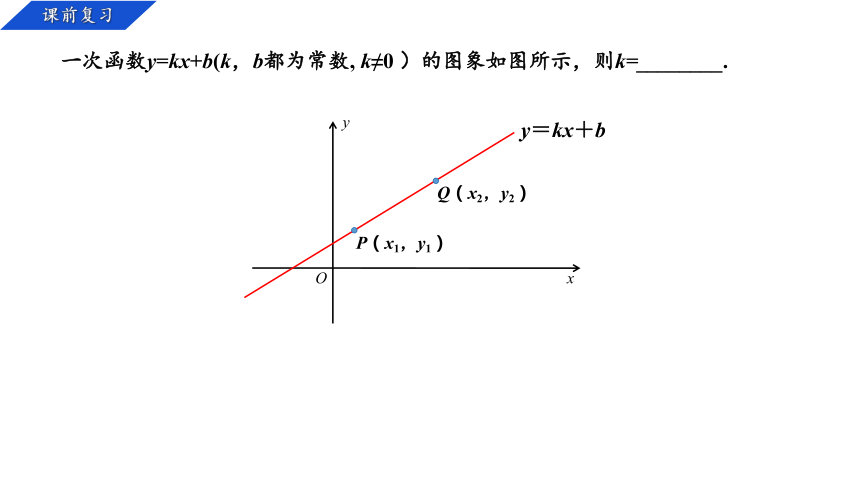
一次函数y=kx+b(k,b都为常数, k≠0 )的图象如图所示,则k=________.
O
P(x1,y1)
x
y
y=kx+b
Q(x2,y2)
课前练习
【练习】已知一次函数y=kx+k﹣1(k为常数且k≠0)
(1)若该图象不经过第二象限,求k的取值范围.
(2)求证:不论k为何值,函数图象都经过一个定点.
(3)在﹣2≤x≤4范围内y有最大值14,求k的值.
解:(1)一次函数y=kx+k﹣1(其中k为常数且k≠0)的图象不经过第二象限,则可能是经过一、三象限或一、三、四象限,经过一、三象限时,k>0且k﹣1=0,此时k=1,经过一、三、四象限时,k>0且k﹣1<0.此时0<k<1综上所述,k的取值范围是:0<k≤1.
(2)过定点(﹣1,﹣1).
(3)k=3或﹣15.
新知探究
【例1】生物学家测得7条成熟的雄性鲸的全长y和吻尖到喷水孔的长度x的数据如下表(单位:m):
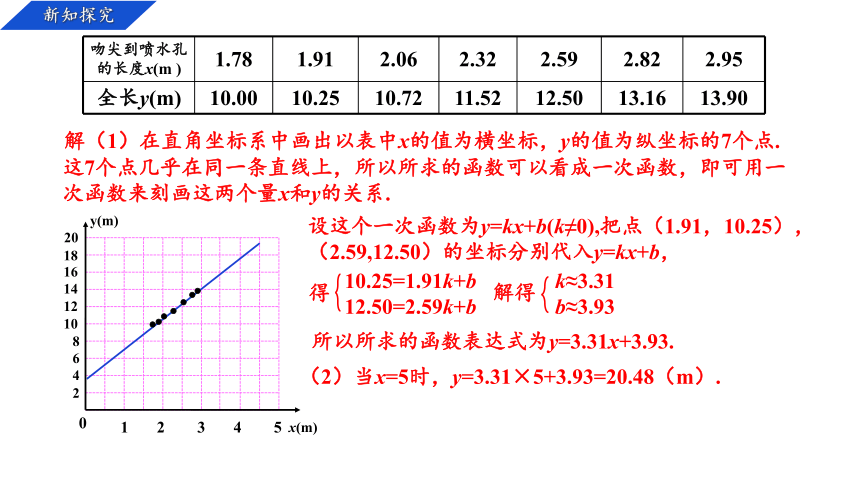
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10.00 10.25 10.72 11.52 12.50 13.16 13.90
(1)问能否用一次函数刻画这两个变量x与y的关系?如果能,请求出这个一次函数的表达式.
(2)根据函数表达式预测出如果雄性鲸的吻尖到喷水孔的长度为5米,则雄性鲸的全长为多少米
新知探究
解(1)在直角坐标系中画出以表中x的值为横坐标,y的值为纵坐标的7个点.
这7个点几乎在同一条直线上,所以所求的函数可以看成一次函数,即可用一次函数来刻画这两个量x和y的关系.
0
1 2 3 4 5
2
4
6
8
10
12
14
16
18
20
y(m)
x(m)
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10.00 10.25 10.72 11.52 12.50 13.16 13.90
设这个一次函数为y=kx+b(k≠0),把点(1.91,10.25),(2.59,12.50)的坐标分别代入y=kx+b,
10.25=1.91k+b
12.50=2.59k+b
得
k≈3.31
b≈3.93
解得
所以所求的函数表达式为y=3.31x+3.93.
(2)当x=5时,y=3.31×5+3.93=20.48(m).
新知探究
【新知1】用一次函数解决实际问题的基本步骤:
(1)先判断问题中的两个变量之间是不是一次函数关系.
(2)求出函数表达式.
(3)运用一次函数的图象和性质进一步解决实际问题.
【新知2】确定两个变量是否构成一次函数的关系的方法(利用图象):
(1)通过实验、测量获得数量足够多的两个变量的对应值.
(2)建立合适的直角坐标系,在坐标系中,以各对应值为坐标描点,并用描点法画出函数图象.
(3)观察图象特征,判定函数的类型.
例题探究
【例1】在某次实验中,测得两个变量m和v之间的4组对应数据如下表:
则m与v之间的关系最接近于下列各函数表达式中的( )
A.v=2m-2 B.v=m2-1
C.v=3m-3 D.v=m+1
m 1 2 3 4
v 0.01 2.9 8.03 15.1
B
例题探究
【例2】联通公司手机话费收费有甲套餐(月租费15元,通话费每分钟0.1元)和乙套餐(月租费0元,通话费每分钟0.15元)两种.设甲套餐每月话费为y1(元),乙套餐每月话费为y2(元),月通话时间为x分钟.(1)分别表示出y1与x,y2与x之间的函数表达式.(2)月通话时间为多长时,甲、乙两种套餐收费一样?(3)什么情况下甲套餐更省钱?
【例3】星期天上午9时,小王出发去他朋友家借书,如图是他离家的距离y(km)与时间x(min)的函数图象.根据图象信息,下列说法中,正确的是 ( )A. 小王去时的速度大于回家的速度B. 小王去朋友家停留了10 minC. 小王去时所花的时间少于回家所花的时间D. 小王在离家1 km处的时间是上午9时10分
例题探究
例题探究
【例4】甲、乙两车同时出发,在同一直线公路上同向匀速行驶,开始甲车在乙车前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后同一时间,甲车继续前行,乙车则原路返回.设甲车行驶x(h)后两车间的距离为y(km),y与x的函数关系如图所示.
(1)请解释图中线段BC的实际意义.
(2)求线段AB所表示的y与x之间的函数表达式.
(3)求甲车与乙车的速度.
【例5】为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.如图折线表示实行阶梯水价后每月水费y(元)与用水量x(m3)之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系.(1)写出点B的实际意义.(2)求线段AB所在直线的函数表达式.(3)某户5月份按照阶梯水价应缴水费102元,其相应用水量为多少立方米?
【解析】(1)图中点B的实际意义表示当用水25 m3时,所缴水费为90元.
(3)设该户5月份用水量为x(m3)(x>90),由(2)知第二阶梯水的单价为4.5元/立方米,则第三阶梯水的单价为6元/立方米.根据题意,得90+6(x-25)=102,解得x=27.
例题探究
学以致用
【1】弹簧挂上物体后伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间有下面的关系:
x 0 1 2 3 4 5 6 7 …
y 12 12.5 13 13.5 14 14.5 15 15.5 …
那么弹簧的总长y(cm)与所挂物体的质量x(kg)之间的函数表达式为 .
学以致用
【2】小聪上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中,小聪离家的路程 s(千米)和经过时间 t(分)之间的函数关系如图所示,请根据图象回答下列问题:
(1)小聪去超市途中的速度是多少 回家途中的速度是多少
(2)小聪在超市逗留了多少时间
(3)小聪在来去途中,离家1千米处的时间是几时几分.
解(1)12km/h,6km/h.
(2)30分.
(3)8:05,8:50.
S=
0.2t
(0≤t≤10)
(40≤t≤60)
-0.1t+6
2
(10
5.5 一次函数的简单应用(1)
第5章 一次函数
浙教版 八年级上册
学习目标
学习目标
(1)了解通过实验获得数据,然后根据数据建立一次函数模型的一般过程.
(2)会综合运用一次函数的表达式,函数图象以及结合方程(组)等其他数学模型,解决实际问题.
课前复习
课前复习
一次函数y=kx+b(k,b都为常数, k≠0 )的图象如图所示,则k=________.
O
P(x1,y1)
x
y
y=kx+b
Q(x2,y2)
课前练习
【练习】已知一次函数y=kx+k﹣1(k为常数且k≠0)
(1)若该图象不经过第二象限,求k的取值范围.
(2)求证:不论k为何值,函数图象都经过一个定点.
(3)在﹣2≤x≤4范围内y有最大值14,求k的值.
解:(1)一次函数y=kx+k﹣1(其中k为常数且k≠0)的图象不经过第二象限,则可能是经过一、三象限或一、三、四象限,经过一、三象限时,k>0且k﹣1=0,此时k=1,经过一、三、四象限时,k>0且k﹣1<0.此时0<k<1综上所述,k的取值范围是:0<k≤1.
(2)过定点(﹣1,﹣1).
(3)k=3或﹣15.
新知探究
【例1】生物学家测得7条成熟的雄性鲸的全长y和吻尖到喷水孔的长度x的数据如下表(单位:m):
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10.00 10.25 10.72 11.52 12.50 13.16 13.90
(1)问能否用一次函数刻画这两个变量x与y的关系?如果能,请求出这个一次函数的表达式.
(2)根据函数表达式预测出如果雄性鲸的吻尖到喷水孔的长度为5米,则雄性鲸的全长为多少米
新知探究
解(1)在直角坐标系中画出以表中x的值为横坐标,y的值为纵坐标的7个点.
这7个点几乎在同一条直线上,所以所求的函数可以看成一次函数,即可用一次函数来刻画这两个量x和y的关系.
0
1 2 3 4 5
2
4
6
8
10
12
14
16
18
20
y(m)
x(m)
吻尖到喷水孔的长度x(m ) 1.78 1.91 2.06 2.32 2.59 2.82 2.95
全长y(m) 10.00 10.25 10.72 11.52 12.50 13.16 13.90
设这个一次函数为y=kx+b(k≠0),把点(1.91,10.25),(2.59,12.50)的坐标分别代入y=kx+b,
10.25=1.91k+b
12.50=2.59k+b
得
k≈3.31
b≈3.93
解得
所以所求的函数表达式为y=3.31x+3.93.
(2)当x=5时,y=3.31×5+3.93=20.48(m).
新知探究
【新知1】用一次函数解决实际问题的基本步骤:
(1)先判断问题中的两个变量之间是不是一次函数关系.
(2)求出函数表达式.
(3)运用一次函数的图象和性质进一步解决实际问题.
【新知2】确定两个变量是否构成一次函数的关系的方法(利用图象):
(1)通过实验、测量获得数量足够多的两个变量的对应值.
(2)建立合适的直角坐标系,在坐标系中,以各对应值为坐标描点,并用描点法画出函数图象.
(3)观察图象特征,判定函数的类型.
例题探究
【例1】在某次实验中,测得两个变量m和v之间的4组对应数据如下表:
则m与v之间的关系最接近于下列各函数表达式中的( )
A.v=2m-2 B.v=m2-1
C.v=3m-3 D.v=m+1
m 1 2 3 4
v 0.01 2.9 8.03 15.1
B
例题探究
【例2】联通公司手机话费收费有甲套餐(月租费15元,通话费每分钟0.1元)和乙套餐(月租费0元,通话费每分钟0.15元)两种.设甲套餐每月话费为y1(元),乙套餐每月话费为y2(元),月通话时间为x分钟.(1)分别表示出y1与x,y2与x之间的函数表达式.(2)月通话时间为多长时,甲、乙两种套餐收费一样?(3)什么情况下甲套餐更省钱?
【例3】星期天上午9时,小王出发去他朋友家借书,如图是他离家的距离y(km)与时间x(min)的函数图象.根据图象信息,下列说法中,正确的是 ( )A. 小王去时的速度大于回家的速度B. 小王去朋友家停留了10 minC. 小王去时所花的时间少于回家所花的时间D. 小王在离家1 km处的时间是上午9时10分
例题探究
例题探究
【例4】甲、乙两车同时出发,在同一直线公路上同向匀速行驶,开始甲车在乙车前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后同一时间,甲车继续前行,乙车则原路返回.设甲车行驶x(h)后两车间的距离为y(km),y与x的函数关系如图所示.
(1)请解释图中线段BC的实际意义.
(2)求线段AB所表示的y与x之间的函数表达式.
(3)求甲车与乙车的速度.
【例5】为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.如图折线表示实行阶梯水价后每月水费y(元)与用水量x(m3)之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系.(1)写出点B的实际意义.(2)求线段AB所在直线的函数表达式.(3)某户5月份按照阶梯水价应缴水费102元,其相应用水量为多少立方米?
【解析】(1)图中点B的实际意义表示当用水25 m3时,所缴水费为90元.
(3)设该户5月份用水量为x(m3)(x>90),由(2)知第二阶梯水的单价为4.5元/立方米,则第三阶梯水的单价为6元/立方米.根据题意,得90+6(x-25)=102,解得x=27.
例题探究
学以致用
【1】弹簧挂上物体后伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间有下面的关系:
x 0 1 2 3 4 5 6 7 …
y 12 12.5 13 13.5 14 14.5 15 15.5 …
那么弹簧的总长y(cm)与所挂物体的质量x(kg)之间的函数表达式为 .
学以致用
【2】小聪上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中,小聪离家的路程 s(千米)和经过时间 t(分)之间的函数关系如图所示,请根据图象回答下列问题:
(1)小聪去超市途中的速度是多少 回家途中的速度是多少
(2)小聪在超市逗留了多少时间
(3)小聪在来去途中,离家1千米处的时间是几时几分.
解(1)12km/h,6km/h.
(2)30分.
(3)8:05,8:50.
S=
0.2t
(0≤t≤10)
(40≤t≤60)
-0.1t+6
2
(10
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
