浙教版初中数学七年级上册6.3线段的长短比较——课后练习(含解析)
文档属性
| 名称 | 浙教版初中数学七年级上册6.3线段的长短比较——课后练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 458.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 08:59:34 | ||
图片预览



文档简介
浙教版初中数学七年级上册6.3线段的长短比较——课后练习
一、选择题
1.下列现象中,可用基本事实“两点之间线段最短”来解释的是( )
A.用两个钉子就可以把木条固定在墙上
B.利用圆规可以比较两条线段的大小关系
C.把弯曲的公路改直,就能缩短路程
D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
2.按语句“画出线段PQ的反向延长线”画图正确的是( )
A. B.
C. D.
3.小王准备从地到地,打开导航,显示两地的距离为,但导航提供的三条可选路线长却分别为,,(如图),下列解释这一现象的数学知识最合理的是( )
A.两点之间,线段最短 B.两点之间,直线最短
C.垂线段最短 D.两点确定一条直线
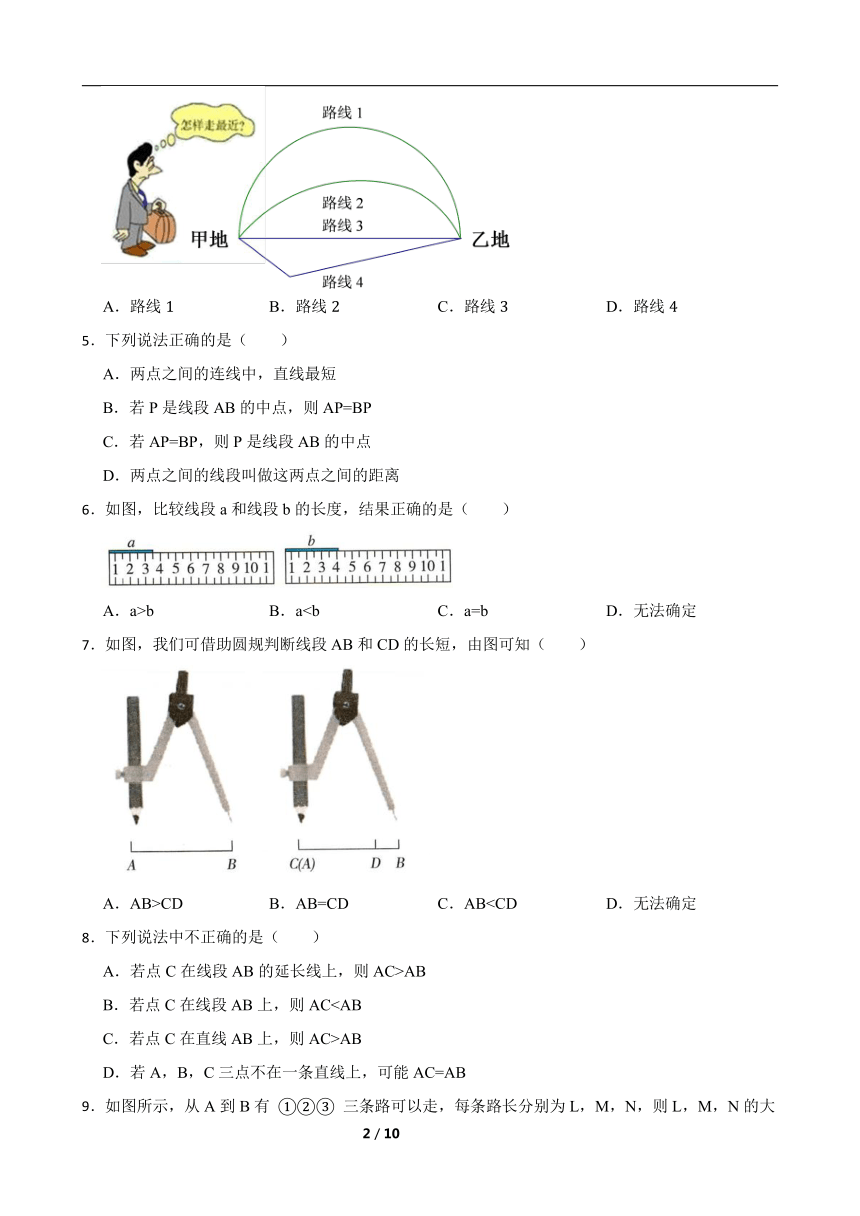
4.如图,从甲地到乙地有四条道路,其中最近的路线是( )
A.路线 B.路线 C.路线 D.路线
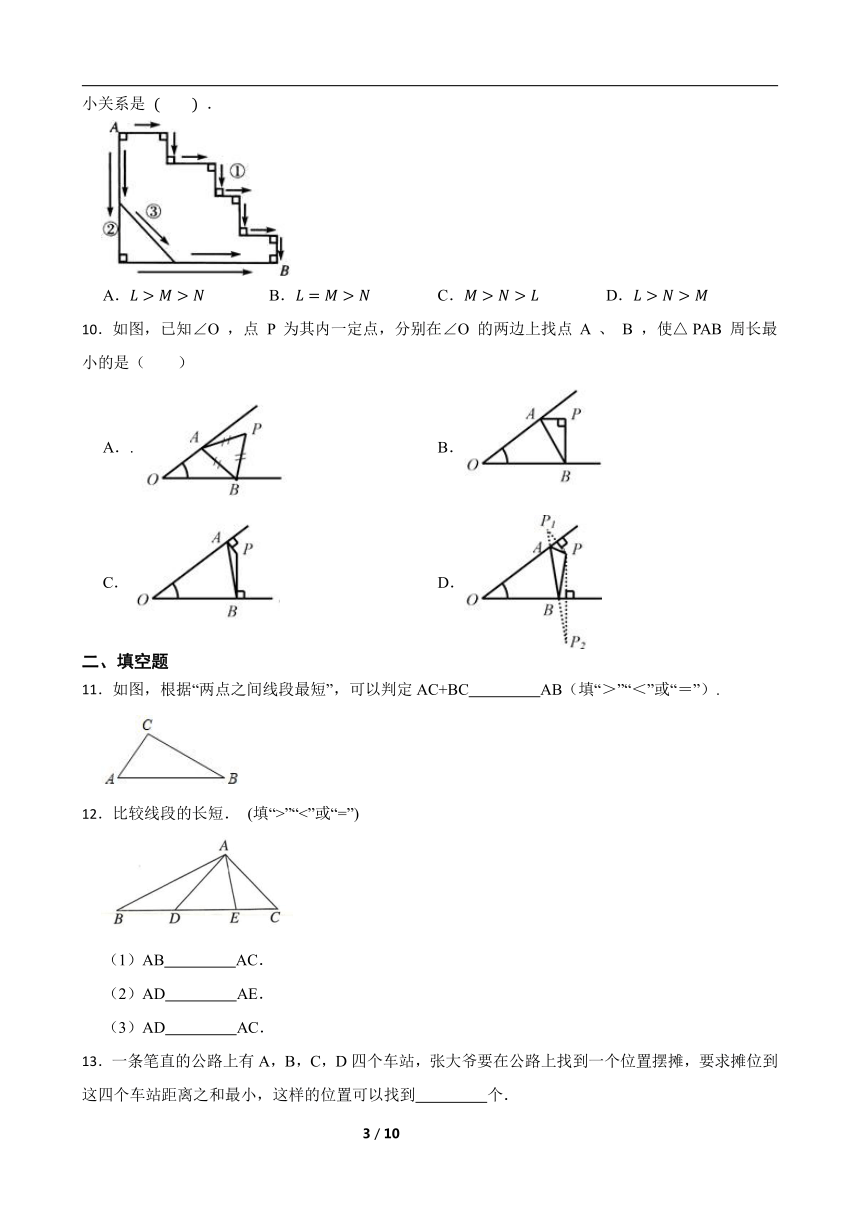
5.下列说法正确的是( )
A.两点之间的连线中,直线最短
B.若P是线段AB的中点,则AP=BP
C.若AP=BP,则P是线段AB的中点
D.两点之间的线段叫做这两点之间的距离
6.如图,比较线段a和线段b的长度,结果正确的是( )
A.a>b B.a7.如图,我们可借助圆规判断线段AB和CD的长短,由图可知( )
A.AB>CD B.AB=CD C.AB8.下列说法中不正确的是( )
A.若点C在线段AB的延长线上,则AC>AB
B.若点C在线段AB上,则ACC.若点C在直线AB上,则AC>AB
D.若A,B,C三点不在一条直线上,可能AC=AB
9.如图所示,从A到B有 三条路可以走,每条路长分别为L,M,N,则L,M,N的大小关系是 .
A. B. C. D.
10.如图,已知∠O ,点 P 为其内一定点,分别在∠O 的两边上找点 A 、 B ,使△ PAB 周长最小的是( )
A.. B.
C. D.
二、填空题
11.如图,根据“两点之间线段最短”,可以判定AC+BC AB(填“>”“<”或“=”).
12.比较线段的长短. (填“>”“<”或“=”)
(1)AB AC.
(2)AD AE.
(3)AD AC.
13.一条笔直的公路上有A,B,C,D四个车站,张大爷要在公路上找到一个位置摆摊,要求摊位到这四个车站距离之和最小,这样的位置可以找到 个.
三、解答题
14.已知:线段a,b
求作:线段AB,使AB=2a+b(用直尺、圆规作图,不写作法,但要保留作图痕迹)
15.景区大楼AB段上有四处居民小区A,B,C,D,且有AC=CD=DB,为改善居民购物的环境,要在AB路建一家超市,每个小区的居民各执一词,难以确定超市的位置,如果由你出任超市负责人,以便民、获利的角度考虑,你将把超市建在哪儿?
16.如图,A,B两个村庄在河MN的两侧,连接AB,与MN相交于点C,点D在MN上,连接AD、BD,且AD=BD,若要在河上建一座桥,使A、B两村来往最便捷,则应该把桥建在点C还是点D?为什么?
17.知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:
你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
答案解析部分
1.【答案】C
【解析】【解答】解:A、用两个钉子就可以把木条固定在墙上,是两点确定一条直线,A错误;
B、利用圆规可以比较两条线段的大小关系,是线段长度比较,B错误;
C、把弯曲的公路改直,就能缩短路程,可用基本事实“两点之间,线段最短”来解释,C正确;
D、植树时,只要定出两棵树的位置,就能确定同一行树所在的直线,是两点确定一条直线,D错误;
故答案为:C.
【分析】根据两点确定一条直线可判断A和D选项说法不符合题意;根据用圆规来比较线段的大小可判断B选项不符合题意;根据两点之间,线段最短可判断C选项说法符合题意;即可得出答案.
2.【答案】B
【解析】【解答】解:画出线段PQ的反向延长线,如图:
故答案为:B.
【分析】根据线段作图的规则,分析即可.
3.【答案】A
【解析】【解答】解:从A地去往B地,打开导航、显示两地距离为10.6km,理由是两点之间线段最短.
故答案为:A.
【分析】根据线段的性质:连接两点的所有线中,线段最短,可得答案.
4.【答案】C
【解析】【解答】解:两点之间线段最短,
∴路线最近,
故答案为:.
【分析】根据“两点之间线段最短”进行解答即可.
5.【答案】B
【解析】【解答】解:A、两点之间的连线中,线段最短,错误;
B、根据中点的定义可知若P是线段AB的中点,则AP=BP,正确;
C、只有当点P在线段AB上,且AP=BP时,点P才是线段AB的中点,错误;
D、连接两点的线段的长度叫做两点的距离,错误.
故选B.
【分析】根据直线的定义、线段中点的性质、点到点的距离的概念利用排除法求解.
6.【答案】B
【解析】【解答】解:根据图示,可得a=3,b=3.5,所以a故答案为:B.
【分析】根据图示,读出长度后比较大小.
7.【答案】A
【解析】【解答】解:由圆规的针尖与笔尖之间的距离不变(相同),AB=CB,CDCD.
故答案为:A.
【分析】由圆规的针尖与笔尖之间的距离不变(相同),结合图形,得出AB与CD的大小关系.
8.【答案】C
【解析】【解答】A.如图, 点C在线段AB的延长线上, AC=AB+BC>AB,即AC>AB,故正确;
B.如图, 若点C在线段AB上, AC=AB-BCC. 点C在直线AB上, 则点C可以在线段AB的延长线上,此时由A知AC>AB,也可以线段AB上,此时由B知ACAB,也可以是ACD.如图, A,B,C三点不在一条直线上,可能AC=AB ,故正确.
故答案为:C.
【分析】分别根据各选项画出图形,再写出式子比较大小,然后判断正确与否,再选出错误的.
9.【答案】B
【解析】【解答】解:根据两点之间线段最短可得第③条路比第②条路短;由于台阶的高度之和就是总体的高度,台阶的长度之和就是总体的长度,所以第①条路和第②条路一样长,所以 ;
故答案为:B.
【分析】利用两点之间线段最短即可判断②和③的长度关系,利用长方形的性质即可判断台阶部分的①和②的长度关系即可求解。
10.【答案】D
【解析】【解答】D图中,三角形的周长=AP+BP+AB=P1A+AB+BP2=P1P2,为一条线段,故为最小,其他三个选项均不是最小周长.
故答案为:D.
【分析】根据两点之间线段最短求出三角形的周长最小值即可。
11.【答案】>
【解析】【解答】解:如图,根据“两点之间线段最短”,可以判定AC+BC>AB,
故答案为:>.
【分析】观察图形可知,利用“两点之间线段最短”可得答案.
12.【答案】(1)>
(2)>
(3)=
【解析】【解答】(1)以A为圆心,AC长为半径作圆弧与AB交于点,如图,可知AB>AC;
(2)以A为圆心,AE长为半径作圆弧与AB交于点,如较,可知AD>AE;
(3)以A为圆心,AD为半径作圆弧,如(1)题的图,可知AD=AC.
故答案为:(1)>;(2)>;(3)=
【分析】由于各对线段都有一个公共顶点,可以以这个端点为圆心,任选一条为半径作圆弧,看第三个点位置判断两线段的长短;也可以用刻度尺分别量出各对线段的长度,再比较大小.
13.【答案】无数
【解析】【解答】解:∵一条笔直的公路上有A,B,C,D四个车站,张大爷要在公路上找到一个位置摆摊,要求摊位到这四个车站距离之和最小,可以建在BC之间的任意一点,
∴这样的位置可以找到无数个.
故答案为:无数
【分析】观察图形可知要使摊位到这四个车站距离之和最小,可得到这个摊位只需建在线段BC段即可.
14.【答案】解:如图:
,
线段AB即为所求.
【解析】【分析】先在射线 上依次截取 再截取 ,则线段
15.【答案】【解答】在线段CD上任取一点M,在线段AC上任取一点N,∵AC=CD=BD,∴当超市的位置在M点时,各居民区到超市和=AM+CM+DM+BM=AB+CD=4CD,当超市的位置在N点时,各居民区到超市的路程和=AN+CN+DN+BN=AB+CD+2CN=4CD+2CN,∵4CD<4CD+2CN,∴以便民、获利的角度考虑,将把超市的位置建在线段CD上的任意一点.【分析】此题需先分别计算出当超市的位置在线段CD上和线段CD外,各居民区到超市的路程和即可确定出超市的位置.
16.【答案】解:建在C点,根据两点之间线段最短,可得建在C点
【解析】【分析】根据两点之间线段最短,得出结论.
17.【答案】解:情景一:因为教学楼和图书馆处于同一条直线上,两点之间的所有连线中,线段最短;
情景二:(需画出图形,并标明P点位置)
理由:两点之间的所有连线中,线段最短.
赞同情景二中运用知识的做法.
【解析】【分析】因为教学楼和图书馆处于同一条直线上,两点之间线段最短;连接AB,使AB两点同在一条直线上,与河流的交点既是最佳位置.
1 / 10
一、选择题
1.下列现象中,可用基本事实“两点之间线段最短”来解释的是( )
A.用两个钉子就可以把木条固定在墙上
B.利用圆规可以比较两条线段的大小关系
C.把弯曲的公路改直,就能缩短路程
D.植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
2.按语句“画出线段PQ的反向延长线”画图正确的是( )
A. B.
C. D.
3.小王准备从地到地,打开导航,显示两地的距离为,但导航提供的三条可选路线长却分别为,,(如图),下列解释这一现象的数学知识最合理的是( )
A.两点之间,线段最短 B.两点之间,直线最短
C.垂线段最短 D.两点确定一条直线
4.如图,从甲地到乙地有四条道路,其中最近的路线是( )
A.路线 B.路线 C.路线 D.路线
5.下列说法正确的是( )
A.两点之间的连线中,直线最短
B.若P是线段AB的中点,则AP=BP
C.若AP=BP,则P是线段AB的中点
D.两点之间的线段叫做这两点之间的距离
6.如图,比较线段a和线段b的长度,结果正确的是( )
A.a>b B.a7.如图,我们可借助圆规判断线段AB和CD的长短,由图可知( )
A.AB>CD B.AB=CD C.AB
A.若点C在线段AB的延长线上,则AC>AB
B.若点C在线段AB上,则AC
D.若A,B,C三点不在一条直线上,可能AC=AB
9.如图所示,从A到B有 三条路可以走,每条路长分别为L,M,N,则L,M,N的大小关系是 .
A. B. C. D.
10.如图,已知∠O ,点 P 为其内一定点,分别在∠O 的两边上找点 A 、 B ,使△ PAB 周长最小的是( )
A.. B.
C. D.
二、填空题
11.如图,根据“两点之间线段最短”,可以判定AC+BC AB(填“>”“<”或“=”).
12.比较线段的长短. (填“>”“<”或“=”)
(1)AB AC.
(2)AD AE.
(3)AD AC.
13.一条笔直的公路上有A,B,C,D四个车站,张大爷要在公路上找到一个位置摆摊,要求摊位到这四个车站距离之和最小,这样的位置可以找到 个.
三、解答题
14.已知:线段a,b
求作:线段AB,使AB=2a+b(用直尺、圆规作图,不写作法,但要保留作图痕迹)
15.景区大楼AB段上有四处居民小区A,B,C,D,且有AC=CD=DB,为改善居民购物的环境,要在AB路建一家超市,每个小区的居民各执一词,难以确定超市的位置,如果由你出任超市负责人,以便民、获利的角度考虑,你将把超市建在哪儿?
16.如图,A,B两个村庄在河MN的两侧,连接AB,与MN相交于点C,点D在MN上,连接AD、BD,且AD=BD,若要在河上建一座桥,使A、B两村来往最便捷,则应该把桥建在点C还是点D?为什么?
17.知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:
你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
答案解析部分
1.【答案】C
【解析】【解答】解:A、用两个钉子就可以把木条固定在墙上,是两点确定一条直线,A错误;
B、利用圆规可以比较两条线段的大小关系,是线段长度比较,B错误;
C、把弯曲的公路改直,就能缩短路程,可用基本事实“两点之间,线段最短”来解释,C正确;
D、植树时,只要定出两棵树的位置,就能确定同一行树所在的直线,是两点确定一条直线,D错误;
故答案为:C.
【分析】根据两点确定一条直线可判断A和D选项说法不符合题意;根据用圆规来比较线段的大小可判断B选项不符合题意;根据两点之间,线段最短可判断C选项说法符合题意;即可得出答案.
2.【答案】B
【解析】【解答】解:画出线段PQ的反向延长线,如图:
故答案为:B.
【分析】根据线段作图的规则,分析即可.
3.【答案】A
【解析】【解答】解:从A地去往B地,打开导航、显示两地距离为10.6km,理由是两点之间线段最短.
故答案为:A.
【分析】根据线段的性质:连接两点的所有线中,线段最短,可得答案.
4.【答案】C
【解析】【解答】解:两点之间线段最短,
∴路线最近,
故答案为:.
【分析】根据“两点之间线段最短”进行解答即可.
5.【答案】B
【解析】【解答】解:A、两点之间的连线中,线段最短,错误;
B、根据中点的定义可知若P是线段AB的中点,则AP=BP,正确;
C、只有当点P在线段AB上,且AP=BP时,点P才是线段AB的中点,错误;
D、连接两点的线段的长度叫做两点的距离,错误.
故选B.
【分析】根据直线的定义、线段中点的性质、点到点的距离的概念利用排除法求解.
6.【答案】B
【解析】【解答】解:根据图示,可得a=3,b=3.5,所以a
【分析】根据图示,读出长度后比较大小.
7.【答案】A
【解析】【解答】解:由圆规的针尖与笔尖之间的距离不变(相同),AB=CB,CD
故答案为:A.
【分析】由圆规的针尖与笔尖之间的距离不变(相同),结合图形,得出AB与CD的大小关系.
8.【答案】C
【解析】【解答】A.如图, 点C在线段AB的延长线上, AC=AB+BC>AB,即AC>AB,故正确;
B.如图, 若点C在线段AB上, AC=AB-BC
故答案为:C.
【分析】分别根据各选项画出图形,再写出式子比较大小,然后判断正确与否,再选出错误的.
9.【答案】B
【解析】【解答】解:根据两点之间线段最短可得第③条路比第②条路短;由于台阶的高度之和就是总体的高度,台阶的长度之和就是总体的长度,所以第①条路和第②条路一样长,所以 ;
故答案为:B.
【分析】利用两点之间线段最短即可判断②和③的长度关系,利用长方形的性质即可判断台阶部分的①和②的长度关系即可求解。
10.【答案】D
【解析】【解答】D图中,三角形的周长=AP+BP+AB=P1A+AB+BP2=P1P2,为一条线段,故为最小,其他三个选项均不是最小周长.
故答案为:D.
【分析】根据两点之间线段最短求出三角形的周长最小值即可。
11.【答案】>
【解析】【解答】解:如图,根据“两点之间线段最短”,可以判定AC+BC>AB,
故答案为:>.
【分析】观察图形可知,利用“两点之间线段最短”可得答案.
12.【答案】(1)>
(2)>
(3)=
【解析】【解答】(1)以A为圆心,AC长为半径作圆弧与AB交于点,如图,可知AB>AC;
(2)以A为圆心,AE长为半径作圆弧与AB交于点,如较,可知AD>AE;
(3)以A为圆心,AD为半径作圆弧,如(1)题的图,可知AD=AC.
故答案为:(1)>;(2)>;(3)=
【分析】由于各对线段都有一个公共顶点,可以以这个端点为圆心,任选一条为半径作圆弧,看第三个点位置判断两线段的长短;也可以用刻度尺分别量出各对线段的长度,再比较大小.
13.【答案】无数
【解析】【解答】解:∵一条笔直的公路上有A,B,C,D四个车站,张大爷要在公路上找到一个位置摆摊,要求摊位到这四个车站距离之和最小,可以建在BC之间的任意一点,
∴这样的位置可以找到无数个.
故答案为:无数
【分析】观察图形可知要使摊位到这四个车站距离之和最小,可得到这个摊位只需建在线段BC段即可.
14.【答案】解:如图:
,
线段AB即为所求.
【解析】【分析】先在射线 上依次截取 再截取 ,则线段
15.【答案】【解答】在线段CD上任取一点M,在线段AC上任取一点N,∵AC=CD=BD,∴当超市的位置在M点时,各居民区到超市和=AM+CM+DM+BM=AB+CD=4CD,当超市的位置在N点时,各居民区到超市的路程和=AN+CN+DN+BN=AB+CD+2CN=4CD+2CN,∵4CD<4CD+2CN,∴以便民、获利的角度考虑,将把超市的位置建在线段CD上的任意一点.【分析】此题需先分别计算出当超市的位置在线段CD上和线段CD外,各居民区到超市的路程和即可确定出超市的位置.
16.【答案】解:建在C点,根据两点之间线段最短,可得建在C点
【解析】【分析】根据两点之间线段最短,得出结论.
17.【答案】解:情景一:因为教学楼和图书馆处于同一条直线上,两点之间的所有连线中,线段最短;
情景二:(需画出图形,并标明P点位置)
理由:两点之间的所有连线中,线段最短.
赞同情景二中运用知识的做法.
【解析】【分析】因为教学楼和图书馆处于同一条直线上,两点之间线段最短;连接AB,使AB两点同在一条直线上,与河流的交点既是最佳位置.
1 / 10
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
