4.4 两个三角形相似的判定 同步练习 2023-2024学年浙教版数学九年级上册(无答案)
文档属性
| 名称 | 4.4 两个三角形相似的判定 同步练习 2023-2024学年浙教版数学九年级上册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 270.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览


文档简介
浙教版九年级上册4.4 两个三角形相似的判定
一、选择题
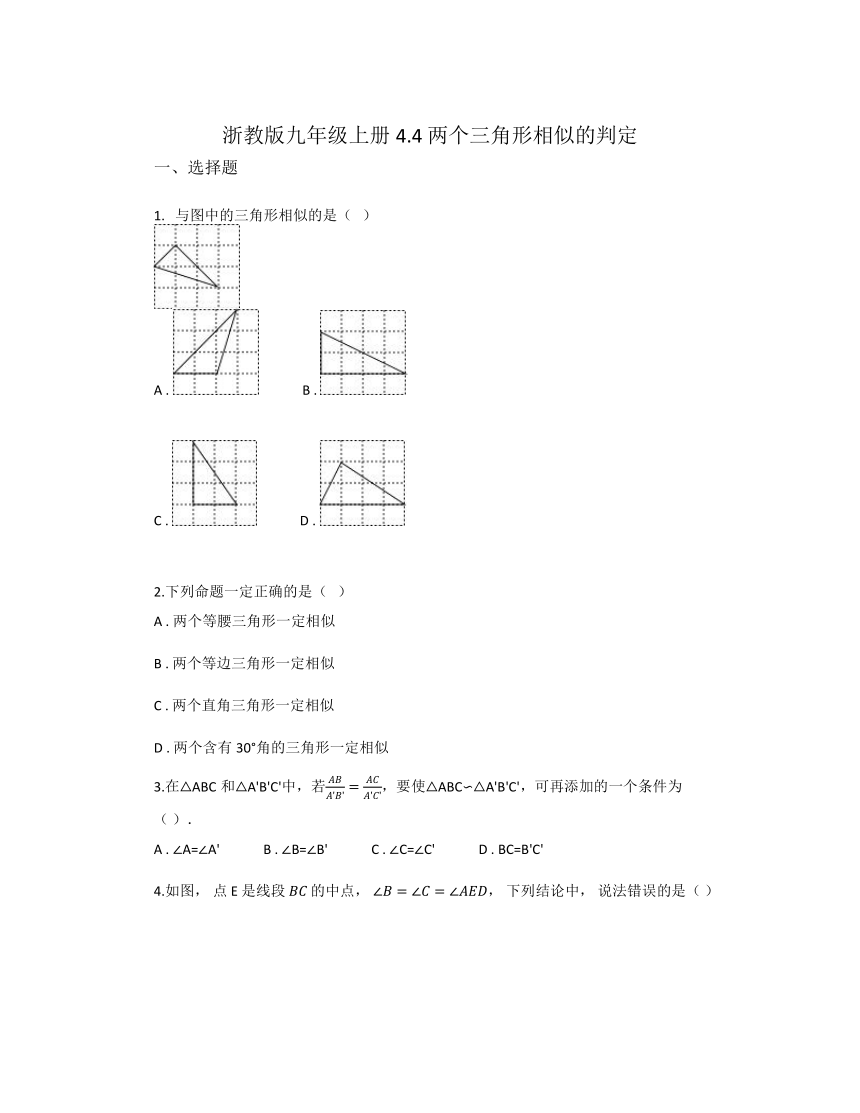
1. 与图中的三角形相似的是( )
A . B .
C . D .
2.下列命题一定正确的是( )
A . 两个等腰三角形一定相似
B . 两个等边三角形一定相似
C . 两个直角三角形一定相似
D . 两个含有30°角的三角形一定相似
3.在△ABC和△A'B'C'中,若,要使△ABC∽△A'B'C',可再添加的一个条件为( ).
A . ∠A=∠A' B . ∠B=∠B' C . ∠C=∠C' D . BC=B'C'
4.如图, 点 E 是线段 的中点, , 下列结论中, 说法错误的是( )
A . 与 相似 B . 与 相似
C . D .
5.如图△ABC和 是以点 为位似中心的位似三角形,若 为 的中点, 面积是 ,则 的面积为( )
A . 10 B . 20 C . 25 D . 50
6.如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形( )
A . 1对 B . 2对 C . 3对 D . 4对
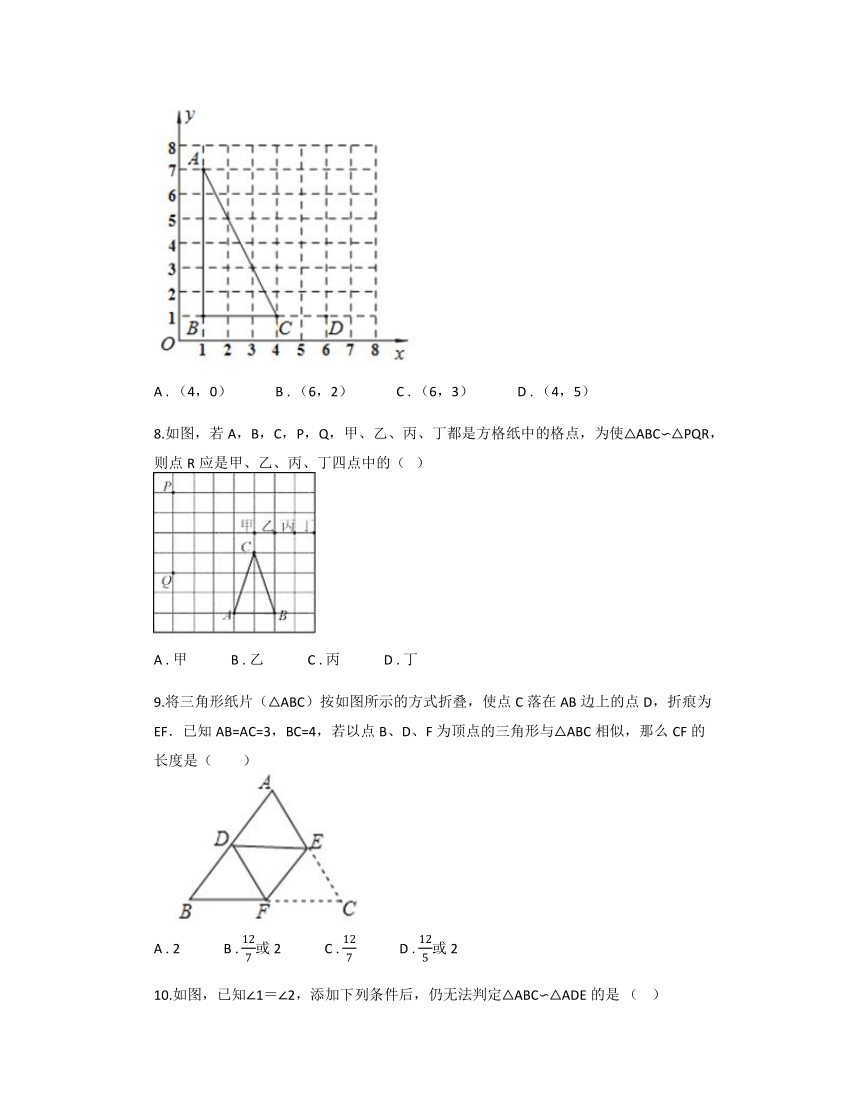
7.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A . (4,0) B . (6,2) C . (6,3) D . (4,5)
8.如图,若A,B,C,P,Q,甲、乙、丙、丁都是方格纸中的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁四点中的( )
A . 甲 B . 乙 C . 丙 D . 丁
9.将三角形纸片(△ABC)按如图所示的方式折叠,使点C落在AB边上的点D,折痕为EF.已知AB=AC=3,BC=4,若以点B、D、F为顶点的三角形与△ABC相似,那么CF的长度是( )
A . 2 B . 或2 C . D . 或2
10.如图,已知∠1=∠2,添加下列条件后,仍无法判定△ABC∽△ADE的是 ( )
A . = B . ∠B=∠D C . ∠C=∠AED D . =
二、填空题
11.如图,∠1=∠2,添加一个条件使得△ADE∽△ACB_____ .
12.如图所示,在△ABC中D为AC边上一点,请你添加一个条件,使△ABC和△BCD相似,你所添加的条件是_____.
13.梯形ABCD中,AD∥BC,AB=DC,点P是AD边上一点,联结PB、PC,且AB2=AP PD,则图中有_____ 对相似三角形.
14.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA= ,则BD的长为_____.
三、解答题
15.图中两个三角形是否相似?为什么?
16.如图,在△ABC中,D为AC边上一点,BC=4,AD=6,CD=2.求证:△BCD∽△ACB.
17.根据学过的两个三角形相似的判定方法,试归纳两个等腰三角形相似的判定方法.两个直角三角形呢?
18.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
19.如图:
(1)[基础巩固]:如图1,在△ABC中,∠ACB=90° ,AC= BC,D是AB边上一点,F是BC边上一点,∠CDF=45°.求证:AC. BF=AD. BD;
(2)[尝试应用]如图2,在四边形ABFC中,点D是AB边的中点,∠A=∠B=∠CDF=45°,若AC=9,BF=8,求线段CF的长.
(3)[拓展提高]如图3,在△ABC中,AB=4 , ∠B=45°.以A为直角顶点作等腰直角三角形ADE,点D在BC上,点E在AC上.若CE=2 , 求CD的长.
一、选择题
1. 与图中的三角形相似的是( )
A . B .
C . D .
2.下列命题一定正确的是( )
A . 两个等腰三角形一定相似
B . 两个等边三角形一定相似
C . 两个直角三角形一定相似
D . 两个含有30°角的三角形一定相似
3.在△ABC和△A'B'C'中,若,要使△ABC∽△A'B'C',可再添加的一个条件为( ).
A . ∠A=∠A' B . ∠B=∠B' C . ∠C=∠C' D . BC=B'C'
4.如图, 点 E 是线段 的中点, , 下列结论中, 说法错误的是( )
A . 与 相似 B . 与 相似
C . D .
5.如图△ABC和 是以点 为位似中心的位似三角形,若 为 的中点, 面积是 ,则 的面积为( )
A . 10 B . 20 C . 25 D . 50
6.如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形( )
A . 1对 B . 2对 C . 3对 D . 4对
7.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A . (4,0) B . (6,2) C . (6,3) D . (4,5)
8.如图,若A,B,C,P,Q,甲、乙、丙、丁都是方格纸中的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁四点中的( )
A . 甲 B . 乙 C . 丙 D . 丁
9.将三角形纸片(△ABC)按如图所示的方式折叠,使点C落在AB边上的点D,折痕为EF.已知AB=AC=3,BC=4,若以点B、D、F为顶点的三角形与△ABC相似,那么CF的长度是( )
A . 2 B . 或2 C . D . 或2
10.如图,已知∠1=∠2,添加下列条件后,仍无法判定△ABC∽△ADE的是 ( )
A . = B . ∠B=∠D C . ∠C=∠AED D . =
二、填空题
11.如图,∠1=∠2,添加一个条件使得△ADE∽△ACB_____ .
12.如图所示,在△ABC中D为AC边上一点,请你添加一个条件,使△ABC和△BCD相似,你所添加的条件是_____.
13.梯形ABCD中,AD∥BC,AB=DC,点P是AD边上一点,联结PB、PC,且AB2=AP PD,则图中有_____ 对相似三角形.
14.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA= ,则BD的长为_____.
三、解答题
15.图中两个三角形是否相似?为什么?
16.如图,在△ABC中,D为AC边上一点,BC=4,AD=6,CD=2.求证:△BCD∽△ACB.
17.根据学过的两个三角形相似的判定方法,试归纳两个等腰三角形相似的判定方法.两个直角三角形呢?
18.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
19.如图:
(1)[基础巩固]:如图1,在△ABC中,∠ACB=90° ,AC= BC,D是AB边上一点,F是BC边上一点,∠CDF=45°.求证:AC. BF=AD. BD;
(2)[尝试应用]如图2,在四边形ABFC中,点D是AB边的中点,∠A=∠B=∠CDF=45°,若AC=9,BF=8,求线段CF的长.
(3)[拓展提高]如图3,在△ABC中,AB=4 , ∠B=45°.以A为直角顶点作等腰直角三角形ADE,点D在BC上,点E在AC上.若CE=2 , 求CD的长.
同课章节目录
