6.4 线段的和差 课件(共23张PPT) 浙教版 七年级数学上册
文档属性
| 名称 | 6.4 线段的和差 课件(共23张PPT) 浙教版 七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 569.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
6.4 线段的和差
浙教版 七年级 上册
教材分析
培养学生的观察力,能把实际问题转化为教学问题,让学生了解线段的和,差概念,会画线段的和差;引导学生理解线段中点的概念,并会用刻度尺画线段的中点;进行有关线段的和,差,倍,分的简单计算.通过实际操作,让学生体会线段的和差在实际生活中的应用.来通过实际操作,让学生体会线段的和差在实际生活中的应用,
教学目标
教学目标:1.理解线段的和差的意义.
2.会用直尺和圆规作两条线段的和与差.
3.理解线段的中点的概念,会用刻度尺二等分一条线段.
4.会进行有关线段的和、差、倍、分的简单计算.
教学重点:线段的和差的概念,这是相关作图和计算的依据.
教学难点:例2涉及较多的线段和较复杂的数量关系,是本节教学中的难点.
新知导入
情境引入
1、度量法——从“数值”的角度比较
2、叠合法——从“形”的角度比较
比较线段长短的两种方法:
起点对齐,看终点
新知讲解
合作学习
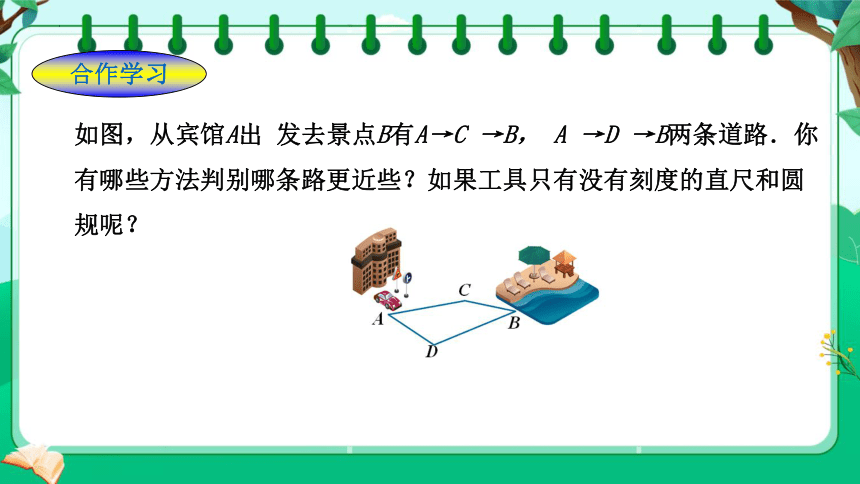
如图,从宾馆A出 发去景点B有A→C →B, A →D →B两条道路.你有哪些方法判别哪条路更近些?如果工具只有没有刻度的直尺和圆规呢?
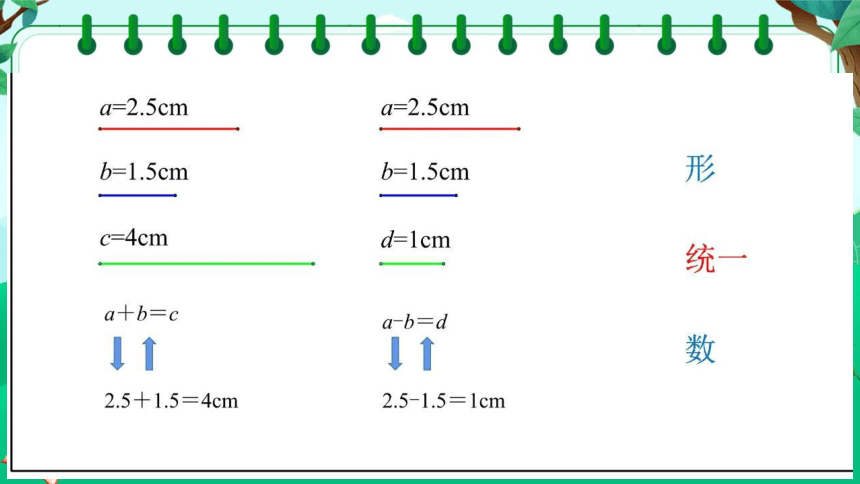
如图,已知线段a=1.5 cm,b=2.5 cm,c=4 cm.
请议一议,a,b,c三条线段的长度之间有怎样的关系?
a+b=1.5+2.5=4,所以a+b=c.
c-a=4-1.5=2.5,所以c-a=b.
c-b=4-2.5=1.5,所以c-b=a.
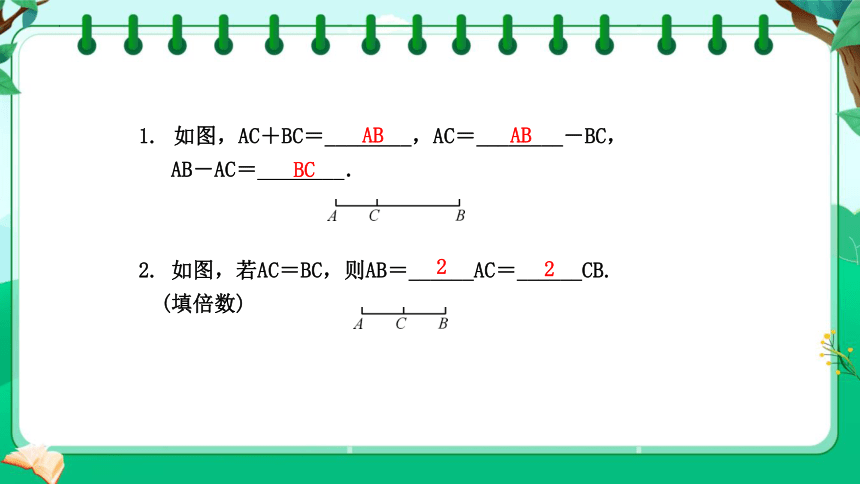
如图,AC+BC=________,AC=________-BC,
AB-AC=________.
2. 如图,若AC=BC,则AB=______AC=______CB.
(填倍数)
AB
AB
BC
2
2
提炼概念
如果一条线段的长度是另两条线段的长度的和,那么这条线段就叫做另两条线段的和;如果一条线段的长度是另两条线段的长度的差,那么这条线段就叫做另两条线段的差.
两条线段的和或差仍是一条线段.
线段c是线段a与b的和,记做c=a+b;线段a是线段c与b的差,记做a=c-b.
典例精讲
例1 已知线段a,b如图.用直尺和圆规,求作:
(1)a+b; (2)b-a.
b
(1)画法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
a
A
D
B
C
线段AC就是所求的线段c.
(2)画法如图:
1.作线段 AB=b.
2.在线段AB上截取AC=a.
线段BC=AB-AC=b-a,线段BC就是所求作的线段.
还有另外的截法吗?
把一条线段分成两条相等的线段的点,叫做这条线段的中点.又叫做二等分点.
如图:若点C把AB分成两条相等的线段,即AC=BC,则点C是线段AB的中点.
几何语言:
∵AC=BC,∴点C是线段AB的中点.
∵AB=2BC,∴点C是线段AB的中点.
∵AC=BC= AB,∴点C是线段AB的中点.
21cnjy.com
几何语言:
∵点C是线段AB的中点,∴AC=BC.
∵点C是线段AB的中点,∴AB=2AC=2BC,
∵点C是线段AB的中点,∴AC=BC= AB.
如图:如果点C是线段AB的中点,那么就有AC=BC.
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.
已知线段CP的长为1.5 cm,求线段AB的长.
分析 如果能得到线段CP与线段AB之间的长度比,就能求出线段AB的长.
解:∵点P是线段AB的中点,
∴AP=BP= AB.
∵点C,D把线段AB三等分,
∴AC=CD=DB= AB.
∴ AB- AB=CP,即CP = AB .
∴AB=6CP=6×1.5=9(cm) .
答:线段AB的长为9 cm.
归纳概念
1、线段的和差实质是线段长度的和差,因此线段间的数量关系就是长度上的数量关系.
2、理解中点的意义和寻找线段间的和差倍分关系是解决线段计算类问题的关键 .
3、用代数设元是解决线段和差问题的一种重要思想.
4、当点之间的相对位置不明确时,应进行分类讨论.
课堂练习
必做题
1、点C在线段AB上,下列条件中不能确定点C是线段AB中点的是( )
A.AC=BC B.AC+BC=AB C.AB=2AC D.BC= AB
2、如图,点B、C在线段AD上,且AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD C.AC=BD D.不能确定
B
C
选做题
3、作图题:已知线段a、b、c(a>b>c)画出一条线段使它等于a-b+c.
解:画法(如图):
①画射线AF;
②在射线AF上截取AB=a;
③在线段AB上截取AC=b,
④在射线BF上截取BD=c,
则线段CD即为所要画的线段.
综合拓展题
4.如图,B,C两点把线段MN分成三部分,其比为MB:BC:CN=2:3:4,P是MN的中点,PC=2 cm,求MN的长.
解:B,C两点把线段MN分成三部分,其比为MB:BC:CN=2:3:4,
设MB=2x,则BC=3x,CN=4x,即MP=4.5x,
故PC=MC-MP=5x-4.5x=0.5x=2 cm,故x=4 cm,
则MN=9x=36 cm.
答:MN=36 cm.
作业布置
必做题
1.如果线段AB=13 cm,MA+MB=17 cm,那么下列说法正确的是( )
A.点M在线段AB上
B.点M在直线AB上
C.点M在直线AB外
D.点M可以在直线AB上,也可以在直线AB外
D
选做题
2.已知数轴上有A,B,C三点,它们所表示的数分别是2,-4,x.
(1)求线段AB的长度;
(2)若AC=5,求x的值.
【解】 (1)AB=2-(-4)=6.
(2)2-x=5,x=-3或x-2=5,x=7.
综合拓展题
3.如图,位于青年大街AB段上有四个居民小区A,C,D,B,其中AC=CD=DB.现想在AB段上建一家超市,要求各居民区到超市的路程总和最小.请你确定超市的位置,并说明你的理由.
解:在线段CD上任取一点M,在线段AC上任取一点N,
∵AC=CD=BD,
∴当超市的位置在M点时,各居民区到超市的路程和=AM+CM+DM+BM=AB+CD=4CD,
当超市的位置在N点时,各居民区到超市的路程和=AN+CN+DN+BN=AB+CD+2CN=4CD+2CN,
∵4CD<4CD+2CN,
∴当超市的位置在线段CD上的任意一点时,各居民区到超市的路程和最小.
6.4 线段的和差
浙教版 七年级 上册
教材分析
培养学生的观察力,能把实际问题转化为教学问题,让学生了解线段的和,差概念,会画线段的和差;引导学生理解线段中点的概念,并会用刻度尺画线段的中点;进行有关线段的和,差,倍,分的简单计算.通过实际操作,让学生体会线段的和差在实际生活中的应用.来通过实际操作,让学生体会线段的和差在实际生活中的应用,
教学目标
教学目标:1.理解线段的和差的意义.
2.会用直尺和圆规作两条线段的和与差.
3.理解线段的中点的概念,会用刻度尺二等分一条线段.
4.会进行有关线段的和、差、倍、分的简单计算.
教学重点:线段的和差的概念,这是相关作图和计算的依据.
教学难点:例2涉及较多的线段和较复杂的数量关系,是本节教学中的难点.
新知导入
情境引入
1、度量法——从“数值”的角度比较
2、叠合法——从“形”的角度比较
比较线段长短的两种方法:
起点对齐,看终点
新知讲解
合作学习
如图,从宾馆A出 发去景点B有A→C →B, A →D →B两条道路.你有哪些方法判别哪条路更近些?如果工具只有没有刻度的直尺和圆规呢?
如图,已知线段a=1.5 cm,b=2.5 cm,c=4 cm.
请议一议,a,b,c三条线段的长度之间有怎样的关系?
a+b=1.5+2.5=4,所以a+b=c.
c-a=4-1.5=2.5,所以c-a=b.
c-b=4-2.5=1.5,所以c-b=a.
如图,AC+BC=________,AC=________-BC,
AB-AC=________.
2. 如图,若AC=BC,则AB=______AC=______CB.
(填倍数)
AB
AB
BC
2
2
提炼概念
如果一条线段的长度是另两条线段的长度的和,那么这条线段就叫做另两条线段的和;如果一条线段的长度是另两条线段的长度的差,那么这条线段就叫做另两条线段的差.
两条线段的和或差仍是一条线段.
线段c是线段a与b的和,记做c=a+b;线段a是线段c与b的差,记做a=c-b.
典例精讲
例1 已知线段a,b如图.用直尺和圆规,求作:
(1)a+b; (2)b-a.
b
(1)画法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
a
A
D
B
C
线段AC就是所求的线段c.
(2)画法如图:
1.作线段 AB=b.
2.在线段AB上截取AC=a.
线段BC=AB-AC=b-a,线段BC就是所求作的线段.
还有另外的截法吗?
把一条线段分成两条相等的线段的点,叫做这条线段的中点.又叫做二等分点.
如图:若点C把AB分成两条相等的线段,即AC=BC,则点C是线段AB的中点.
几何语言:
∵AC=BC,∴点C是线段AB的中点.
∵AB=2BC,∴点C是线段AB的中点.
∵AC=BC= AB,∴点C是线段AB的中点.
21cnjy.com
几何语言:
∵点C是线段AB的中点,∴AC=BC.
∵点C是线段AB的中点,∴AB=2AC=2BC,
∵点C是线段AB的中点,∴AC=BC= AB.
如图:如果点C是线段AB的中点,那么就有AC=BC.
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.
已知线段CP的长为1.5 cm,求线段AB的长.
分析 如果能得到线段CP与线段AB之间的长度比,就能求出线段AB的长.
解:∵点P是线段AB的中点,
∴AP=BP= AB.
∵点C,D把线段AB三等分,
∴AC=CD=DB= AB.
∴ AB- AB=CP,即CP = AB .
∴AB=6CP=6×1.5=9(cm) .
答:线段AB的长为9 cm.
归纳概念
1、线段的和差实质是线段长度的和差,因此线段间的数量关系就是长度上的数量关系.
2、理解中点的意义和寻找线段间的和差倍分关系是解决线段计算类问题的关键 .
3、用代数设元是解决线段和差问题的一种重要思想.
4、当点之间的相对位置不明确时,应进行分类讨论.
课堂练习
必做题
1、点C在线段AB上,下列条件中不能确定点C是线段AB中点的是( )
A.AC=BC B.AC+BC=AB C.AB=2AC D.BC= AB
2、如图,点B、C在线段AD上,且AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD C.AC=BD D.不能确定
B
C
选做题
3、作图题:已知线段a、b、c(a>b>c)画出一条线段使它等于a-b+c.
解:画法(如图):
①画射线AF;
②在射线AF上截取AB=a;
③在线段AB上截取AC=b,
④在射线BF上截取BD=c,
则线段CD即为所要画的线段.
综合拓展题
4.如图,B,C两点把线段MN分成三部分,其比为MB:BC:CN=2:3:4,P是MN的中点,PC=2 cm,求MN的长.
解:B,C两点把线段MN分成三部分,其比为MB:BC:CN=2:3:4,
设MB=2x,则BC=3x,CN=4x,即MP=4.5x,
故PC=MC-MP=5x-4.5x=0.5x=2 cm,故x=4 cm,
则MN=9x=36 cm.
答:MN=36 cm.
作业布置
必做题
1.如果线段AB=13 cm,MA+MB=17 cm,那么下列说法正确的是( )
A.点M在线段AB上
B.点M在直线AB上
C.点M在直线AB外
D.点M可以在直线AB上,也可以在直线AB外
D
选做题
2.已知数轴上有A,B,C三点,它们所表示的数分别是2,-4,x.
(1)求线段AB的长度;
(2)若AC=5,求x的值.
【解】 (1)AB=2-(-4)=6.
(2)2-x=5,x=-3或x-2=5,x=7.
综合拓展题
3.如图,位于青年大街AB段上有四个居民小区A,C,D,B,其中AC=CD=DB.现想在AB段上建一家超市,要求各居民区到超市的路程总和最小.请你确定超市的位置,并说明你的理由.
解:在线段CD上任取一点M,在线段AC上任取一点N,
∵AC=CD=BD,
∴当超市的位置在M点时,各居民区到超市的路程和=AM+CM+DM+BM=AB+CD=4CD,
当超市的位置在N点时,各居民区到超市的路程和=AN+CN+DN+BN=AB+CD+2CN=4CD+2CN,
∵4CD<4CD+2CN,
∴当超市的位置在线段CD上的任意一点时,各居民区到超市的路程和最小.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
