2.8 直角三角形全等的判定 同步练习(无答案) 浙教版八年级数学上册
文档属性
| 名称 | 2.8 直角三角形全等的判定 同步练习(无答案) 浙教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 136.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览

文档简介
浙教版八年级上册2.8 直角三角形全等的判定
一、选择题
1.下列条件不可以判定两个直角三角形全等的是( )
A . 两条直角边对应相等 B . 斜边和一直角边对应相等
C . 斜边和一锐角对应相等 D . 两个角对应相等
2.下列说法错误的是( )
A . 在Rt△ABC中两锐角互余
B . 有两个锐角不互余的三角形不是直角三角形
C . 两边对应相等的两直角三角形全等
D . 周长相等的两个直角三角形全等
3.下列判断正确的是( )
A . 有一条直角边对应相等的两个直角三角形全等
B . 腰长相等的两个等腰三角形全等
C . 斜边相等的两个等腰直角三角形全等
D . 两个锐角对应相等的两个直角三角形全等
4.如图,∠BAD=∠BCD=90°,AB=CB,可以证明△BAD≌△BCD的理由是( )
A . HL B . ASA C . SAS D . AAS
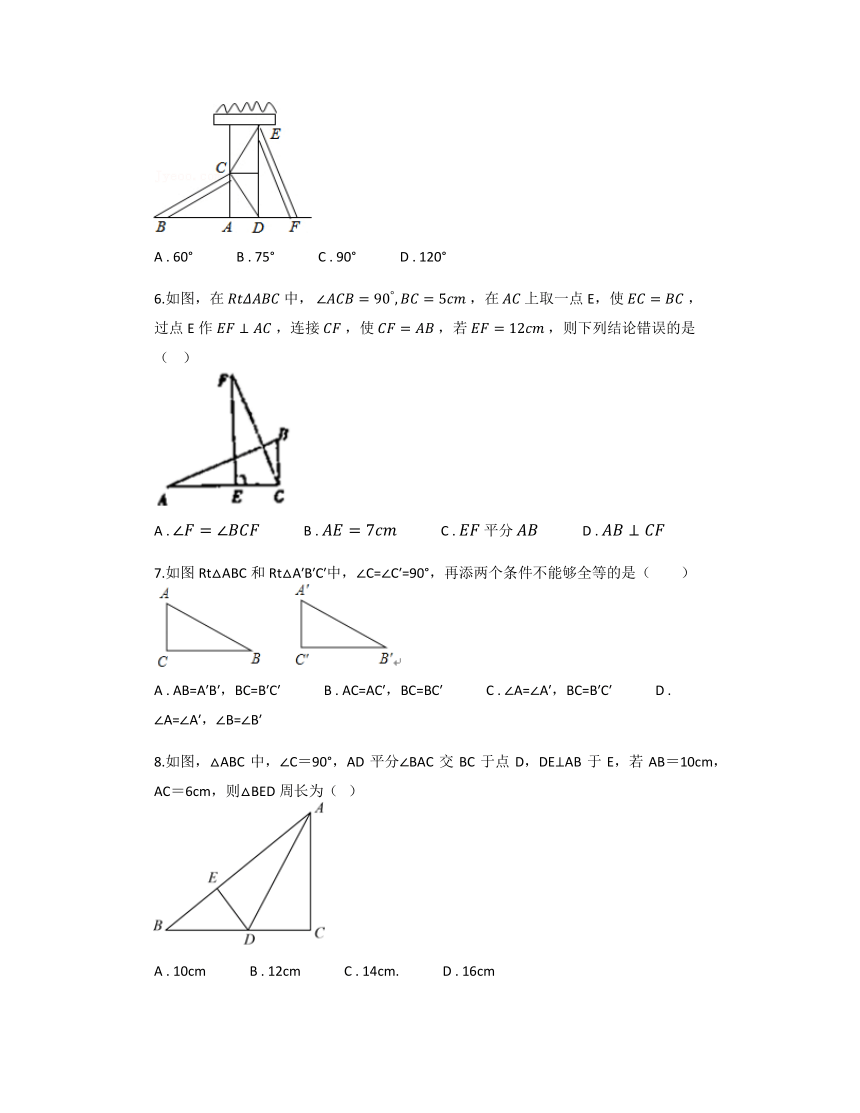
5.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为( )
A . 60° B . 75° C . 90° D . 120°
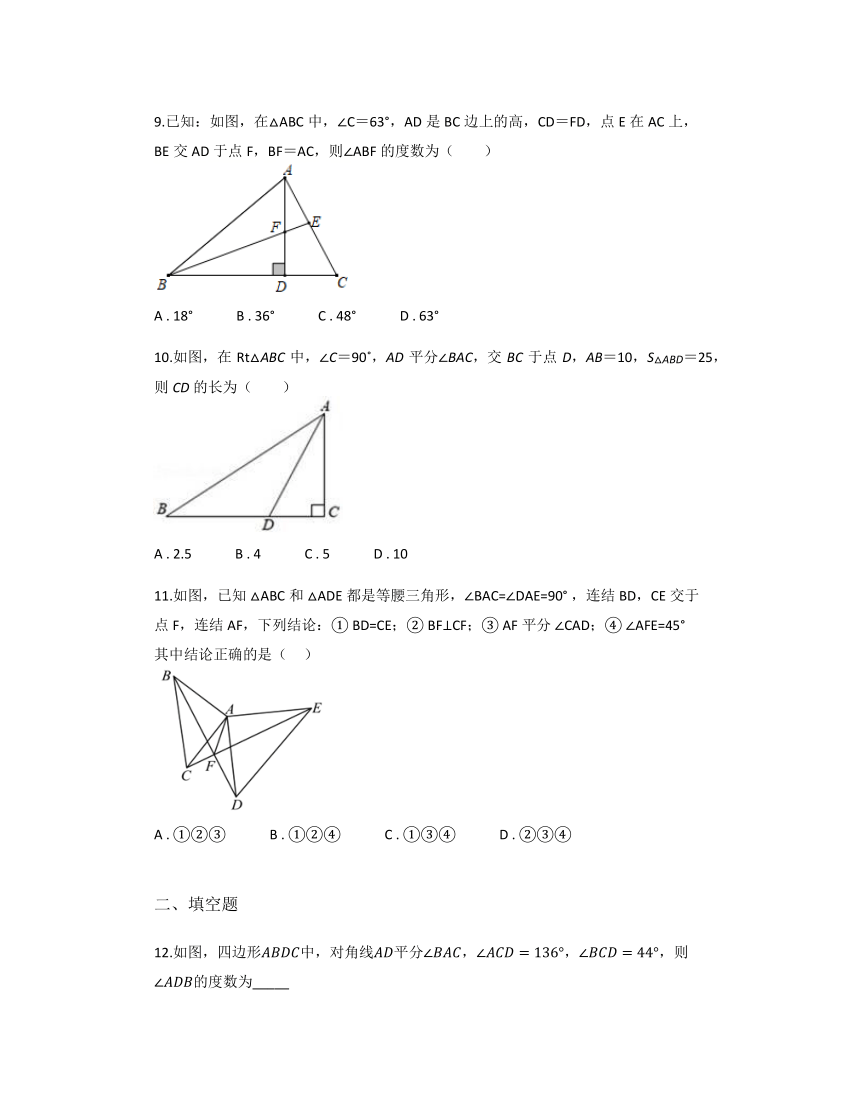
6.如图,在 中, ,在 上取一点E,使 ,过点E作 ,连接 ,使 ,若 ,则下列结论错误的是( )
A . B . C . 平分 D .
7.如图Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,再添两个条件不能够全等的是( )
A . AB=A′B′,BC=B′C′ B . AC=AC′,BC=BC′ C . ∠A=∠A′,BC=B′C′ D . ∠A=∠A′,∠B=∠B′
8.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于E,若AB=10cm,AC=6cm,则△BED周长为( )
A . 10cm B . 12cm C . 14cm. D . 16cm
9.已知:如图,在△ABC中,∠C=63°,AD是BC边上的高,CD=FD,点E在AC上,BE交AD于点F,BF=AC,则∠ABF的度数为( )
A . 18° B . 36° C . 48° D . 63°
10.如图,在Rt△ABC中,∠C=90 ,AD平分∠BAC,交BC于点D,AB=10,S△ABD=25,则CD的长为( )
A . 2.5 B . 4 C . 5 D . 10
11.如图,已知 △ABC和 △ADE都是等腰三角形,∠BAC=∠DAE=90° ,连结BD,CE交于点F,连结AF,下列结论:① BD=CE;② BF⊥CF;③ AF平分 ∠CAD;④ ∠AFE=45°
其中结论正确的是( )
A . ①②③ B . ①②④ C . ①③④ D . ②③④
二、填空题
12.如图,四边形中,对角线平分,,,则的度数为_____
13.如图, 和 中, ,在不添加任何辅助线和字母的情况下,请你添加一个条件_____使 和 全等.
14.
如图所示,△ABC和△DCB有公共边BC,且AB=DC,作AE⊥BC,DF⊥BC,垂足分别为E、F,AE=DF,那么求证AC=BD时,需要证明三角形全等的三角形是 _____
15.如图,在 中, , ,分别以A和B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN分别交AB、AC于点F、D,作 于E.有下面三个结论:①BD平分 ;② ;③ 其中,正确的结论的是_____
三、解答题
16.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,
求证:AD是∠BAC的平分线.
17.已知:如图∠BAC的角平分线与BC的垂直平分线交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.
18.已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF,求证:AD∥BC
19.要将图中的 平分,小强设计如下方案:
在射线 , 上分别取 ,过点A作 于A,交 于D;过点 作 于点B,交 于E, , 交于点C,过点O、点C作射线 ,射线 即为 的平分线.请说明这样做的理由.
20.随着几何部分的学习,小明对几何产生了浓厚的兴趣,他最喜欢利用手中的工具画图了.如图,作一个∠AOB,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接OP.小明通过观察和推理,得出结论:OP平分∠AOB.你同意小明的观点吗?如果你同意,试结合题意与图形写出已知和求证,并证明;如果不同意请说明理由.
一、选择题
1.下列条件不可以判定两个直角三角形全等的是( )
A . 两条直角边对应相等 B . 斜边和一直角边对应相等
C . 斜边和一锐角对应相等 D . 两个角对应相等
2.下列说法错误的是( )
A . 在Rt△ABC中两锐角互余
B . 有两个锐角不互余的三角形不是直角三角形
C . 两边对应相等的两直角三角形全等
D . 周长相等的两个直角三角形全等
3.下列判断正确的是( )
A . 有一条直角边对应相等的两个直角三角形全等
B . 腰长相等的两个等腰三角形全等
C . 斜边相等的两个等腰直角三角形全等
D . 两个锐角对应相等的两个直角三角形全等
4.如图,∠BAD=∠BCD=90°,AB=CB,可以证明△BAD≌△BCD的理由是( )
A . HL B . ASA C . SAS D . AAS
5.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的度数和为( )
A . 60° B . 75° C . 90° D . 120°
6.如图,在 中, ,在 上取一点E,使 ,过点E作 ,连接 ,使 ,若 ,则下列结论错误的是( )
A . B . C . 平分 D .
7.如图Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,再添两个条件不能够全等的是( )
A . AB=A′B′,BC=B′C′ B . AC=AC′,BC=BC′ C . ∠A=∠A′,BC=B′C′ D . ∠A=∠A′,∠B=∠B′
8.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于E,若AB=10cm,AC=6cm,则△BED周长为( )
A . 10cm B . 12cm C . 14cm. D . 16cm
9.已知:如图,在△ABC中,∠C=63°,AD是BC边上的高,CD=FD,点E在AC上,BE交AD于点F,BF=AC,则∠ABF的度数为( )
A . 18° B . 36° C . 48° D . 63°
10.如图,在Rt△ABC中,∠C=90 ,AD平分∠BAC,交BC于点D,AB=10,S△ABD=25,则CD的长为( )
A . 2.5 B . 4 C . 5 D . 10
11.如图,已知 △ABC和 △ADE都是等腰三角形,∠BAC=∠DAE=90° ,连结BD,CE交于点F,连结AF,下列结论:① BD=CE;② BF⊥CF;③ AF平分 ∠CAD;④ ∠AFE=45°
其中结论正确的是( )
A . ①②③ B . ①②④ C . ①③④ D . ②③④
二、填空题
12.如图,四边形中,对角线平分,,,则的度数为_____
13.如图, 和 中, ,在不添加任何辅助线和字母的情况下,请你添加一个条件_____使 和 全等.
14.
如图所示,△ABC和△DCB有公共边BC,且AB=DC,作AE⊥BC,DF⊥BC,垂足分别为E、F,AE=DF,那么求证AC=BD时,需要证明三角形全等的三角形是 _____
15.如图,在 中, , ,分别以A和B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN分别交AB、AC于点F、D,作 于E.有下面三个结论:①BD平分 ;② ;③ 其中,正确的结论的是_____
三、解答题
16.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,
求证:AD是∠BAC的平分线.
17.已知:如图∠BAC的角平分线与BC的垂直平分线交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.
18.已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF,求证:AD∥BC
19.要将图中的 平分,小强设计如下方案:
在射线 , 上分别取 ,过点A作 于A,交 于D;过点 作 于点B,交 于E, , 交于点C,过点O、点C作射线 ,射线 即为 的平分线.请说明这样做的理由.
20.随着几何部分的学习,小明对几何产生了浓厚的兴趣,他最喜欢利用手中的工具画图了.如图,作一个∠AOB,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接OP.小明通过观察和推理,得出结论:OP平分∠AOB.你同意小明的观点吗?如果你同意,试结合题意与图形写出已知和求证,并证明;如果不同意请说明理由.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
