4.3用乘法公式分解因式(2) 课件

课件14张PPT。4.3 用乘法公式因式分解（2）岭头中学 王万贵把下列各式分解因式首项有负常提负
各项有公先提公
分解因式要彻底（1） － ax4+ax2
（2）16m4－n4a2?b2 = (a+b)(a?b)回顾自主导学1.填空：
(1)（a+b)2 =_____ 反之a2+2ab+b2=________
(2)（a-b)2= _____
a2-2ab+b2=________ 两数的平方和，加上（或者减去）这两数的
积的2倍，等于 。a2+2ab+b2（a+b)2 a2-2ab+b2（a-b)2请用语言来叙述上述两个公式的特征.形如 a2+2ab+b2 或 a2-2ab+b 2完全平方数式
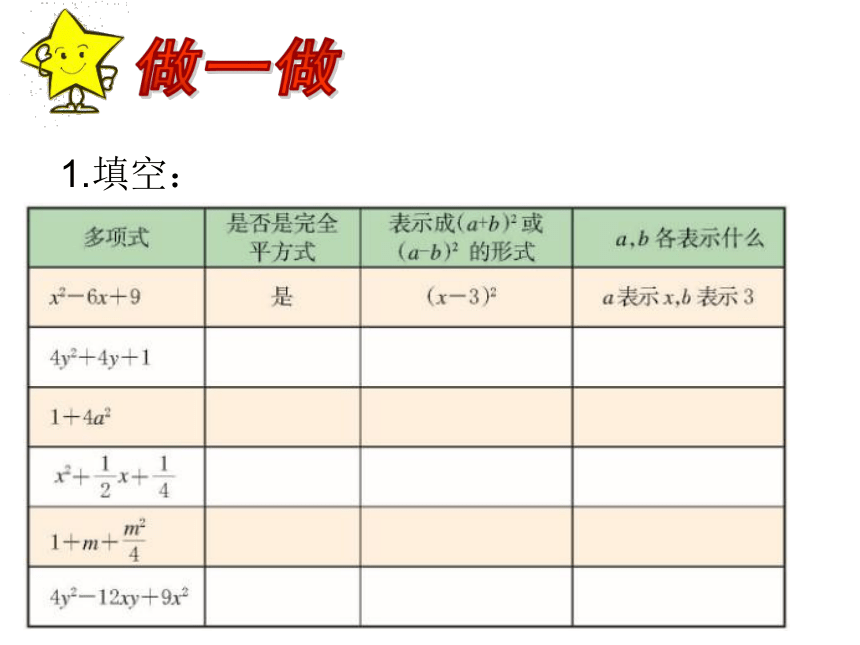
做一做1.填空：
做一做2.按照完全平方公式填空.
(1)?a2-10a+(??? ????)=(??? ???)2.
(2) (????? ??)+2ay+1=(???? ??)2.
(3) -( )+r2s2=( )2.
(4) m2+16m+( )= ( )2. 3.下列多项式中,哪些是完全平方式? 将完全平方式进行因式分解. 做一做(1)?m2+4m+4.? (2)?m2n2-4+4mn.(3)??x+1+? ?.? ?(4)?9p2-24pq+16q2. 总结：完全平方式的特征：
形如( )2+2( )( )+( )2或( )2-2( )( )+( )2
（1）是一个三项式；
（2）两项同号且是某数或某式的平方；
（3）还有一项是两个数的积的2倍.试一试例1.把下列各式分解因式:
(1)16a2+24ab+9b2.????? (2)?-x2+8xy-16y2.
(3)?4ax2+8axy+4ay2. (4)(3x-y)2-6(3x-y)+9.课堂练习1.分解因式:
(1)? 4a2+24a+36.?????????????????????????
(2)?-a2-10a-25.
(3)?49b2+a2+14ab．???????
(4)?4x3y+4x2y2+xy3．
(5)?x4-18x2+81．
(6)(a-b)2-10(a-b)+25. 课堂练习2.下面的因式分解对吗?为什么?
(1)?m2+n2=(m+n)2.????????????????? ?
(2)?m2-n2=(m-n)2.
(3)?a2+2ab-b2=(a-b)2.????? ???
(4)?-a2-2ab-b2=-(a-b)2.（1）形如________________形式的两次三项式可以用完全平方公式分解因式。（3）因式分解要_________（2）因式分解通常先考虑______________方法。再考虑 _____________ 方法。课堂小结提取公因式法公式法彻底 因式分解顺口流
若要分解多项式，先看有无公因式；
看到两次两项式，就用平方差公式；
遇到两次三项式，应用完全平方式；
结果都是积整式，彻底分解多项式。
探究展示1.用简便方法计算:20152- 4030×2013+20132. 2.将4x2+1再加上一项,使它成为(a+b)2的形式.?你有几种方法? 探究活动观察下表，你还能继续往下写吗？你发现了什么规律？能用因式分解来说明你发现的规律吗？任何一个正奇数都可以表示成两个相邻自然数的平方差。对于正奇数2n+1(n为自然数)，有布置作业
1、作业本（1）
2、课文P108作业题