浙教版初中数学八年级上册第五章一次函数——单元练习 (含答案)
文档属性
| 名称 | 浙教版初中数学八年级上册第五章一次函数——单元练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 670.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 00:00:00 | ||
图片预览

文档简介
浙教版初中数学八年级上册第五章一次函数——单元练习
一、选择题
1.下列函数中,是一次函数的是( )
A. B. C. D.
2.已知一次函数经过点,则下列不在该函数图象上的点是( )
A. B. C. D.
3.直线的图象与轴的交点坐标为( )
A. B. C. D.
4.一次函数的图象过点,,则和的大小关系是( )
A. B. C. D.无法确定
5.对于一次函数,下列说法不正确的是( )
A.图象与的图象平行 B.图像不经过第三象限
C.图象与坐标轴围成的面积是2 D.当时,
6.将直线平移后,得到直线,则原直线( )
A.沿轴向上平移了7个单位 B.沿轴向下平移了7个单位
C.沿轴向左平移了7个单位 D.沿轴向右平移了7个单位
7.如图,在平面直角坐标系中,线段的端点坐标为,,直线与线段有交点,则的值不可能是( )
A.-5 B.-2 C.3 D.5
8.把直线向上平移n个单位后,与直线的交点在第二象限,则n的取值范围是( )
A. B. C. D.
9.已知一次函数与(,为常数,且),则它们在同一平面直角坐标系内的图象可能为( )
A. B.
C. D.
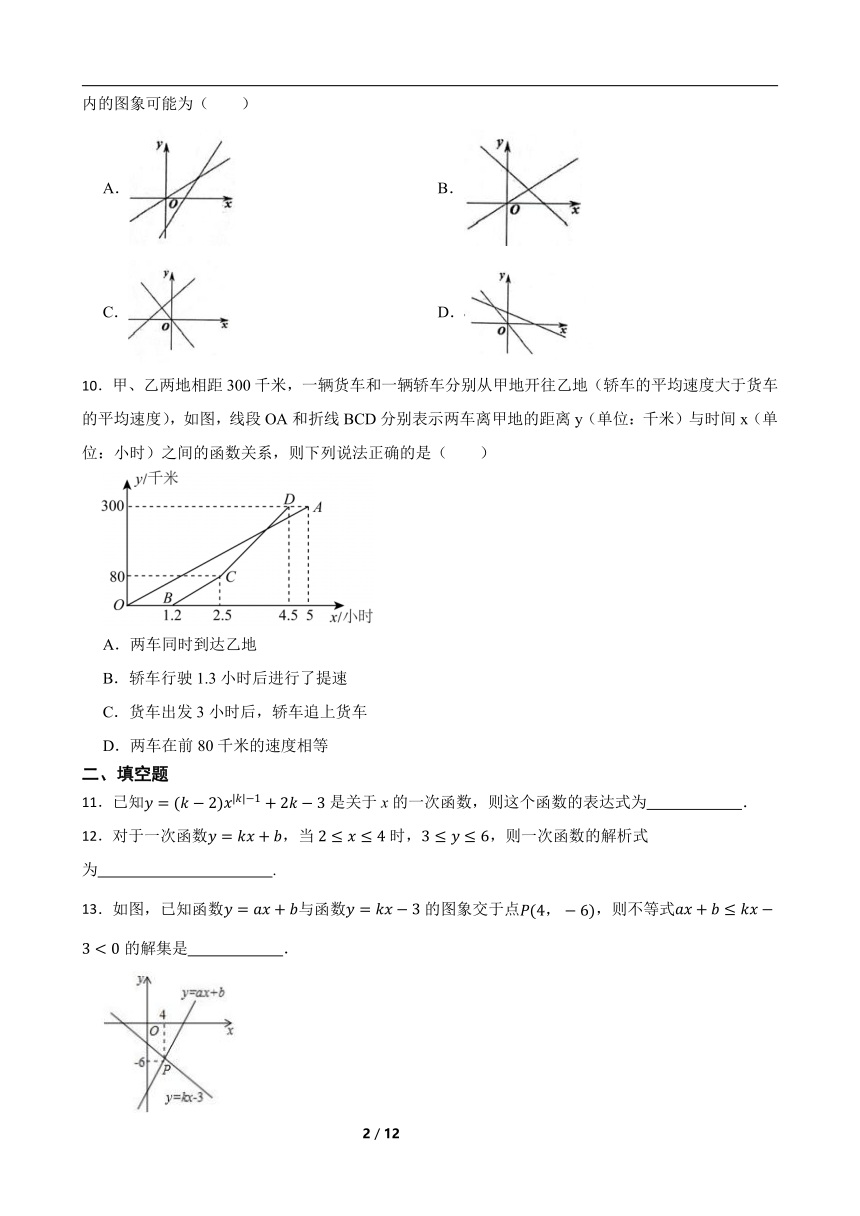
10.甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地(轿车的平均速度大于货车的平均速度),如图,线段OA和折线BCD分别表示两车离甲地的距离y(单位:千米)与时间x(单位:小时)之间的函数关系,则下列说法正确的是( )
A.两车同时到达乙地
B.轿车行驶1.3小时后进行了提速
C.货车出发3小时后,轿车追上货车
D.两车在前80千米的速度相等
二、填空题
11.已知是关于x的一次函数,则这个函数的表达式为 .
12.对于一次函数,当时,,则一次函数的解析式为 .
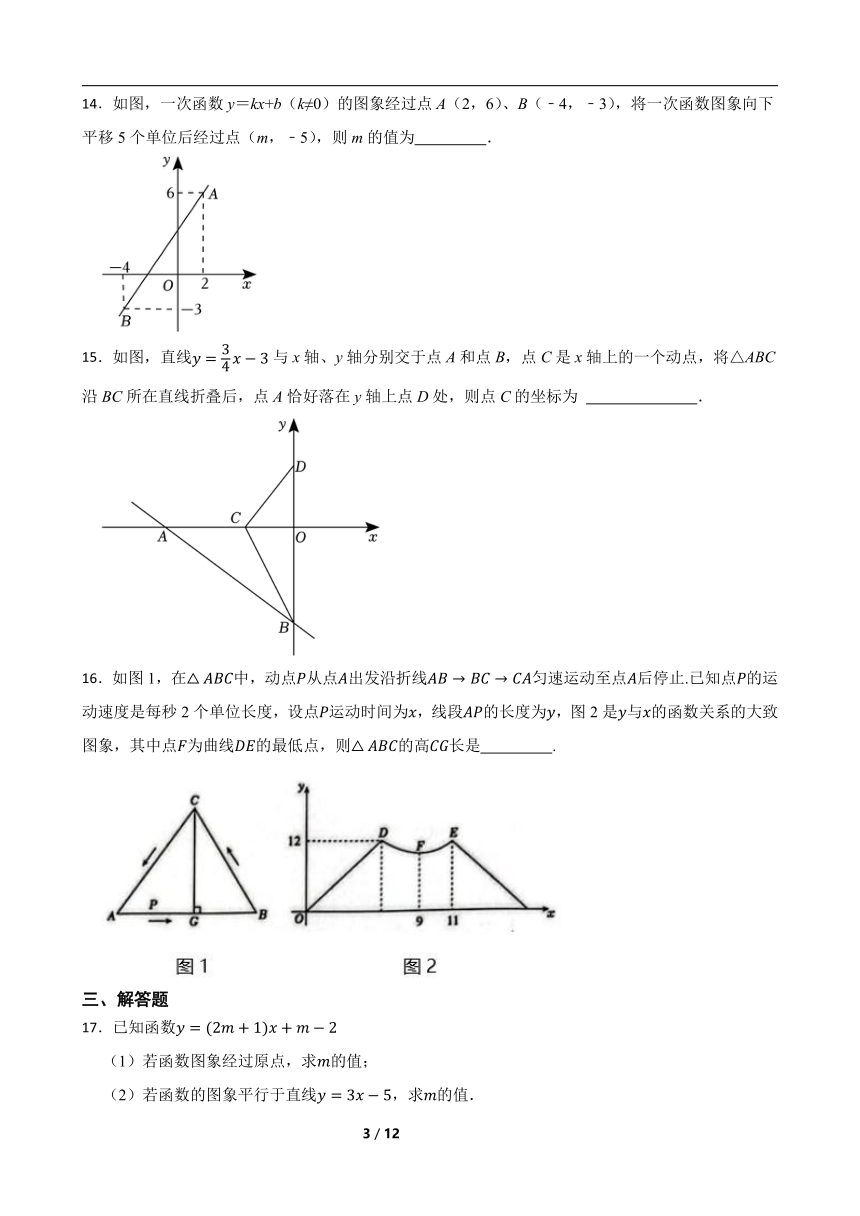
13.如图,已知函数与函数的图象交于点,则不等式的解集是 .
14.如图,一次函数y=kx+b(k≠0)的图象经过点A(2,6)、B(﹣4,﹣3),将一次函数图象向下平移5个单位后经过点(m,﹣5),则m的值为 .
15.如图,直线与x轴、y轴分别交于点A和点B,点C是x轴上的一个动点,将△ABC沿BC所在直线折叠后,点A恰好落在y轴上点D处,则点C的坐标为 .
16.如图1,在中,动点从点出发沿折线匀速运动至点后停止.已知点的运动速度是每秒2个单位长度,设点运动时间为,线段的长度为,图2是与的函数关系的大致图象,其中点为曲线的最低点,则的高长是 .
三、解答题
17.已知函数
(1)若函数图象经过原点,求的值;
(2)若函数的图象平行于直线,求的值.
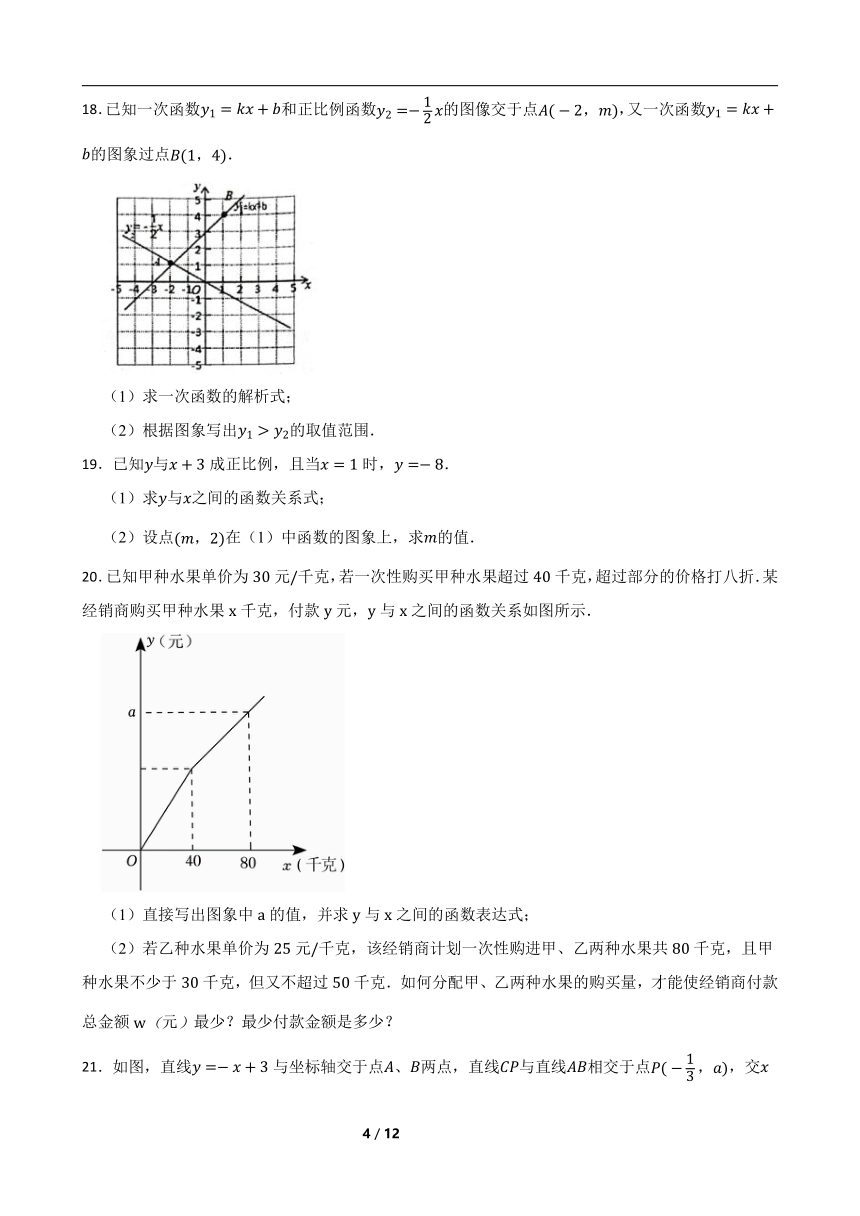
18.已知一次函数和正比例函数的图像交于点,又一次函数的图象过点.
(1)求一次函数的解析式;
(2)根据图象写出的取值范围.
19.已知与成正比例,且当时,.
(1)求与之间的函数关系式;
(2)设点在(1)中函数的图象上,求的值.
20.已知甲种水果单价为元千克,若一次性购买甲种水果超过千克,超过部分的价格打八折.某经销商购买甲种水果千克,付款元,与之间的函数关系如图所示.
(1)直接写出图象中的值,并求与之间的函数表达式;
(2)若乙种水果单价为元千克,该经销商计划一次性购进甲、乙两种水果共千克,且甲种水果不少于千克,但又不超过千克.如何分配甲、乙两种水果的购买量,才能使经销商付款总金额元最少?最少付款金额是多少?
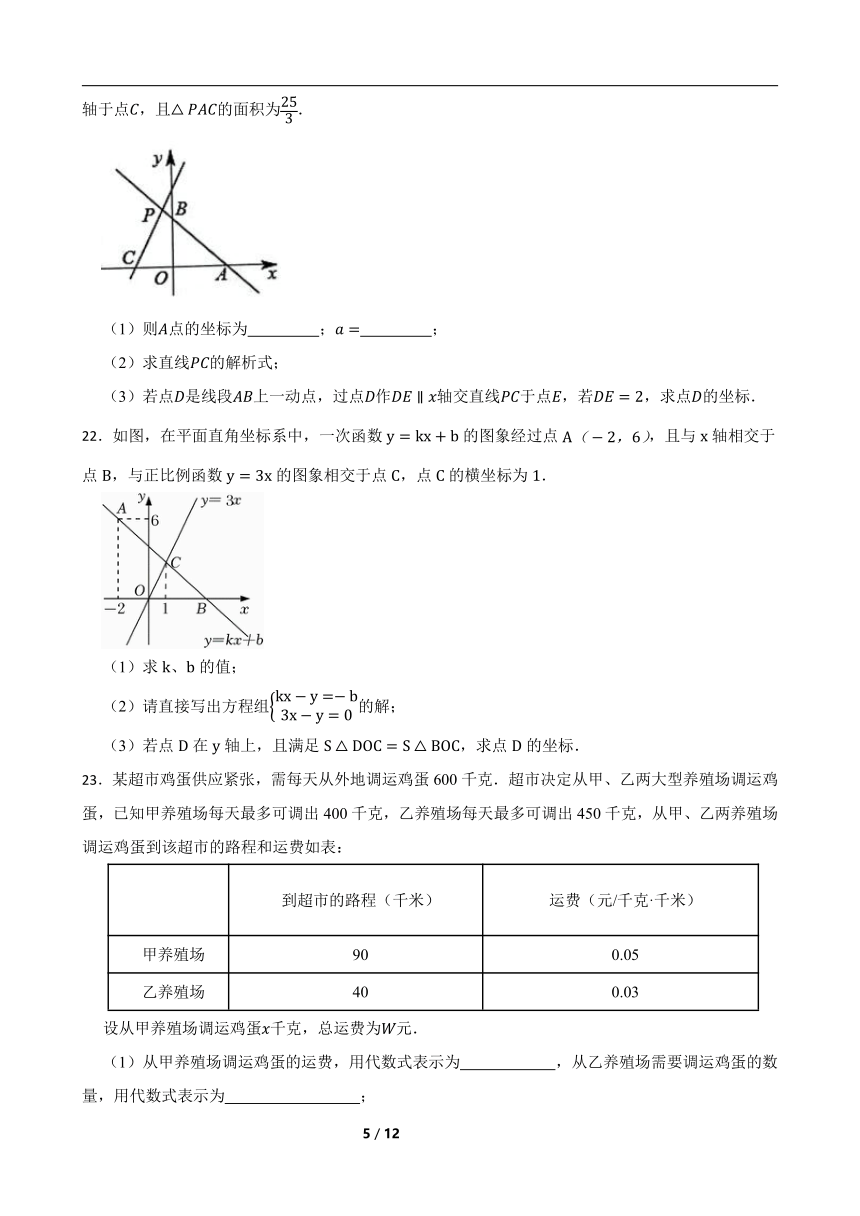
21.如图,直线与坐标轴交于点、两点,直线与直线相交于点,交轴于点,且的面积为.
(1)则点的坐标为 ; ;
(2)求直线的解析式;
(3)若点是线段上一动点,过点作轴交直线于点,若,求点的坐标.
22.如图,在平面直角坐标系中,一次函数的图象经过点,且与轴相交于点,与正比例函数的图象相交于点,点的横坐标为.
(1)求、的值;
(2)请直接写出方程组的解;
(3)若点在轴上,且满足,求点的坐标.
23.某超市鸡蛋供应紧张,需每天从外地调运鸡蛋600千克.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出400千克,乙养殖场每天最多可调出450千克,从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如表:
到超市的路程(千米) 运费(元/千克·千米)
甲养殖场 90 0.05
乙养殖场 40 0.03
设从甲养殖场调运鸡蛋千克,总运费为元.
(1)从甲养殖场调运鸡蛋的运费,用代数式表示为 ,从乙养殖场需要调运鸡蛋的数量,用代数式表示为 ;
(2)试写出与的函数关系式;
(3)请求出自变量取值范围,说明怎样安排调运方案才能使每天的总运费最少?
答案解析部分
1.【答案】B
【解析】【解答】解:A是二次函数,不符合题意;
B是一次函数,符合题意;
C是分式函数,不符合题意;
D是分式函数,不符合题意.
故答案为:B
【分析】根据一次函数的定义即可求出答案.
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】D
6.【答案】A
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
11.【答案】
12.【答案】或
【解析】【解答】解:当k>0时,一次函数y=kx+b是增函数,
∵当时,,
∴当x=2时,y=3;当x=4时,y=6,
∴,
解得:,
一次函数的解析式为 : ;
当k<0时,一次函数y=kx+b是减函数,
∵当时,,
∴当x=2时,y=6;当x=4时,y=3,
同理求得一次函数的解析式为: 。
∴一次函数的解析式为:或 。
故答案为: 或 .
【分析】根据待定系数法,由于k的符号不能确定,故应对k>0和k<0两种情况进行解答.
13.【答案】
14.【答案】﹣2
【解析】【解答】解: 把点A(2,6)、B(﹣4,﹣3)代入y=kx+b(k≠0)中,
∴,
解得:k=,b=3,
∴y=x+3
∴一次函数图象向下平移5个单位得到y=x+3-5,即y=x-2,
把点(m,﹣5) 代入y=x-2中,得m-2=-5,
解得:m=-2,
故答案为:-2.
【分析】利用待定系数法求出一次函数解析式,进一步求出平移后的解析式,再将点(m,5)代入即可求解.
15.【答案】
16.【答案】
【解析】【解答】解:如图过点A作AQ⊥BC于点Q,当点P与Q重合时,在图2中F点表示当AB+ BQ=9时,点P到达点Q,此时当P在BC上运动时,AP最小,
∴AB= 12,
∵点的运动速度是每秒2个单位长度,
∴点D的横坐标为6,
∴BC=2×(11-6)=10,BQ =2×(9-6)=6,
在Rt△ABQ中,AB= 12,BQ=6,
∴AQ===,
∵S△ABC=AB × CG=AQ × BC,
∴=;
故答案为:.
【分析】过点A作AQ⊥BC于点Q,当点P与Q重合时,在图2中F点表示当AB+BQ=9时,点P到达点Q,此时当P在BC上运动时,AP
最小,勾股定理求得AQ然后等面积法即可求解.
17.【答案】(1)解:
(2)解:
18.【答案】(1)解:把点代入得,则A点坐标为,
把、代入得,
解得,所以
(2)解:如图,当x>﹣2时,y1>y2.
19.【答案】(1)解:设y=k(x+3)(k≠0),则-8=k(1+3),k=-2,∴y=-2x-6
(2)解:当y=2时,即-2m-6=2,∴m=-4
20.【答案】(1)解:;当时,,
当时,
设.
将坐标和代入,
得
解得,
.
综上,
(2)解:设购进甲种水果千克,则购进乙种水果千克.
当时,
,
随的减小而减小,
当时,取最小值,此时,
.
当时,
,
随的增大而减小,
当时,取最小值,此时,
.
综上,,
购进甲、乙两种水果分别为千克、千克,才能使经销商付款总金额最少,最少付款金额是元.
21.【答案】(1);
(2)解:过点作轴,垂足为,如图;
由(1)得:,
,
即,,,
点的坐标为.
设直线的解析式为,
将点、代入得:
,解得:,
直线的解析式为
(3)解:如图:
设点的坐标为,
轴交直线于点,,
点的坐标为,
代入直线的解析式为得,,
解得,
当时,,
点的坐标为.
22.【答案】(1)解:当时,,
点坐标为.
直线经过和,
则,
解得
(2)解:
(3)解:当时,,
,
,
设点坐标为,
.
,
,
解得,
点的坐标为或
23.【答案】(1)元;千克
(2)解:根据题意得:,
与的函数关系式为
(3)解:由题意得,,,
由(2)知,
,
随的增大而增大,
当时,取得最小值,此时,
此时,
答:当从甲养殖场调运150斤鸡蛋,从乙养殖场调运450斤鸡蛋时,每天的总运费最省,总运费最低是1215元.
12 / 12
一、选择题
1.下列函数中,是一次函数的是( )
A. B. C. D.
2.已知一次函数经过点,则下列不在该函数图象上的点是( )
A. B. C. D.
3.直线的图象与轴的交点坐标为( )
A. B. C. D.
4.一次函数的图象过点,,则和的大小关系是( )
A. B. C. D.无法确定
5.对于一次函数,下列说法不正确的是( )
A.图象与的图象平行 B.图像不经过第三象限
C.图象与坐标轴围成的面积是2 D.当时,
6.将直线平移后,得到直线,则原直线( )
A.沿轴向上平移了7个单位 B.沿轴向下平移了7个单位
C.沿轴向左平移了7个单位 D.沿轴向右平移了7个单位
7.如图,在平面直角坐标系中,线段的端点坐标为,,直线与线段有交点,则的值不可能是( )
A.-5 B.-2 C.3 D.5
8.把直线向上平移n个单位后,与直线的交点在第二象限,则n的取值范围是( )
A. B. C. D.
9.已知一次函数与(,为常数,且),则它们在同一平面直角坐标系内的图象可能为( )
A. B.
C. D.
10.甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地(轿车的平均速度大于货车的平均速度),如图,线段OA和折线BCD分别表示两车离甲地的距离y(单位:千米)与时间x(单位:小时)之间的函数关系,则下列说法正确的是( )
A.两车同时到达乙地
B.轿车行驶1.3小时后进行了提速
C.货车出发3小时后,轿车追上货车
D.两车在前80千米的速度相等
二、填空题
11.已知是关于x的一次函数,则这个函数的表达式为 .
12.对于一次函数,当时,,则一次函数的解析式为 .
13.如图,已知函数与函数的图象交于点,则不等式的解集是 .
14.如图,一次函数y=kx+b(k≠0)的图象经过点A(2,6)、B(﹣4,﹣3),将一次函数图象向下平移5个单位后经过点(m,﹣5),则m的值为 .
15.如图,直线与x轴、y轴分别交于点A和点B,点C是x轴上的一个动点,将△ABC沿BC所在直线折叠后,点A恰好落在y轴上点D处,则点C的坐标为 .
16.如图1,在中,动点从点出发沿折线匀速运动至点后停止.已知点的运动速度是每秒2个单位长度,设点运动时间为,线段的长度为,图2是与的函数关系的大致图象,其中点为曲线的最低点,则的高长是 .
三、解答题
17.已知函数
(1)若函数图象经过原点,求的值;
(2)若函数的图象平行于直线,求的值.
18.已知一次函数和正比例函数的图像交于点,又一次函数的图象过点.
(1)求一次函数的解析式;
(2)根据图象写出的取值范围.
19.已知与成正比例,且当时,.
(1)求与之间的函数关系式;
(2)设点在(1)中函数的图象上,求的值.
20.已知甲种水果单价为元千克,若一次性购买甲种水果超过千克,超过部分的价格打八折.某经销商购买甲种水果千克,付款元,与之间的函数关系如图所示.
(1)直接写出图象中的值,并求与之间的函数表达式;
(2)若乙种水果单价为元千克,该经销商计划一次性购进甲、乙两种水果共千克,且甲种水果不少于千克,但又不超过千克.如何分配甲、乙两种水果的购买量,才能使经销商付款总金额元最少?最少付款金额是多少?
21.如图,直线与坐标轴交于点、两点,直线与直线相交于点,交轴于点,且的面积为.
(1)则点的坐标为 ; ;
(2)求直线的解析式;
(3)若点是线段上一动点,过点作轴交直线于点,若,求点的坐标.
22.如图,在平面直角坐标系中,一次函数的图象经过点,且与轴相交于点,与正比例函数的图象相交于点,点的横坐标为.
(1)求、的值;
(2)请直接写出方程组的解;
(3)若点在轴上,且满足,求点的坐标.
23.某超市鸡蛋供应紧张,需每天从外地调运鸡蛋600千克.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出400千克,乙养殖场每天最多可调出450千克,从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如表:
到超市的路程(千米) 运费(元/千克·千米)
甲养殖场 90 0.05
乙养殖场 40 0.03
设从甲养殖场调运鸡蛋千克,总运费为元.
(1)从甲养殖场调运鸡蛋的运费,用代数式表示为 ,从乙养殖场需要调运鸡蛋的数量,用代数式表示为 ;
(2)试写出与的函数关系式;
(3)请求出自变量取值范围,说明怎样安排调运方案才能使每天的总运费最少?
答案解析部分
1.【答案】B
【解析】【解答】解:A是二次函数,不符合题意;
B是一次函数,符合题意;
C是分式函数,不符合题意;
D是分式函数,不符合题意.
故答案为:B
【分析】根据一次函数的定义即可求出答案.
2.【答案】C
3.【答案】A
4.【答案】C
5.【答案】D
6.【答案】A
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
11.【答案】
12.【答案】或
【解析】【解答】解:当k>0时,一次函数y=kx+b是增函数,
∵当时,,
∴当x=2时,y=3;当x=4时,y=6,
∴,
解得:,
一次函数的解析式为 : ;
当k<0时,一次函数y=kx+b是减函数,
∵当时,,
∴当x=2时,y=6;当x=4时,y=3,
同理求得一次函数的解析式为: 。
∴一次函数的解析式为:或 。
故答案为: 或 .
【分析】根据待定系数法,由于k的符号不能确定,故应对k>0和k<0两种情况进行解答.
13.【答案】
14.【答案】﹣2
【解析】【解答】解: 把点A(2,6)、B(﹣4,﹣3)代入y=kx+b(k≠0)中,
∴,
解得:k=,b=3,
∴y=x+3
∴一次函数图象向下平移5个单位得到y=x+3-5,即y=x-2,
把点(m,﹣5) 代入y=x-2中,得m-2=-5,
解得:m=-2,
故答案为:-2.
【分析】利用待定系数法求出一次函数解析式,进一步求出平移后的解析式,再将点(m,5)代入即可求解.
15.【答案】
16.【答案】
【解析】【解答】解:如图过点A作AQ⊥BC于点Q,当点P与Q重合时,在图2中F点表示当AB+ BQ=9时,点P到达点Q,此时当P在BC上运动时,AP最小,
∴AB= 12,
∵点的运动速度是每秒2个单位长度,
∴点D的横坐标为6,
∴BC=2×(11-6)=10,BQ =2×(9-6)=6,
在Rt△ABQ中,AB= 12,BQ=6,
∴AQ===,
∵S△ABC=AB × CG=AQ × BC,
∴=;
故答案为:.
【分析】过点A作AQ⊥BC于点Q,当点P与Q重合时,在图2中F点表示当AB+BQ=9时,点P到达点Q,此时当P在BC上运动时,AP
最小,勾股定理求得AQ然后等面积法即可求解.
17.【答案】(1)解:
(2)解:
18.【答案】(1)解:把点代入得,则A点坐标为,
把、代入得,
解得,所以
(2)解:如图,当x>﹣2时,y1>y2.
19.【答案】(1)解:设y=k(x+3)(k≠0),则-8=k(1+3),k=-2,∴y=-2x-6
(2)解:当y=2时,即-2m-6=2,∴m=-4
20.【答案】(1)解:;当时,,
当时,
设.
将坐标和代入,
得
解得,
.
综上,
(2)解:设购进甲种水果千克,则购进乙种水果千克.
当时,
,
随的减小而减小,
当时,取最小值,此时,
.
当时,
,
随的增大而减小,
当时,取最小值,此时,
.
综上,,
购进甲、乙两种水果分别为千克、千克,才能使经销商付款总金额最少,最少付款金额是元.
21.【答案】(1);
(2)解:过点作轴,垂足为,如图;
由(1)得:,
,
即,,,
点的坐标为.
设直线的解析式为,
将点、代入得:
,解得:,
直线的解析式为
(3)解:如图:
设点的坐标为,
轴交直线于点,,
点的坐标为,
代入直线的解析式为得,,
解得,
当时,,
点的坐标为.
22.【答案】(1)解:当时,,
点坐标为.
直线经过和,
则,
解得
(2)解:
(3)解:当时,,
,
,
设点坐标为,
.
,
,
解得,
点的坐标为或
23.【答案】(1)元;千克
(2)解:根据题意得:,
与的函数关系式为
(3)解:由题意得,,,
由(2)知,
,
随的增大而增大,
当时,取得最小值,此时,
此时,
答:当从甲养殖场调运150斤鸡蛋,从乙养殖场调运450斤鸡蛋时,每天的总运费最省,总运费最低是1215元.
12 / 12
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
