2023--2024学年浙教版初中数学九年级上册第一章二次函数——期末基础复习试题(含解析)
文档属性
| 名称 | 2023--2024学年浙教版初中数学九年级上册第一章二次函数——期末基础复习试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 281.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 00:00:00 | ||
图片预览



文档简介
浙教版初中数学九年级上册第一章二次函数——期末基础复习
一、选择题
1.下列函数解析式中,一定为二次函数的是( )
A. B. C. D.
2.格二次函数y=2x2+4x-6化成y=a(x-h)2+k的形式为( )
A.y=2(x-1)2+8 B.y= 2(x+1)2-4
C.y=2(x+1)2-8 D.y=2(x+2)2-10
3.若 , , 为二次函数 的图象上的三点,则 , , 的大小关系是 .
A. B. C. D.
4.抛物线y=2x2+4x +5与坐标轴的交点个数为( )
(A) (B) (C) (D)
A.0个 B.1个 C.2个 D.3个
5.在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )
A. B.
C. D.
6. 根据下列表格对应值:
判断关于x的方程的一个解x的范围是( )
A. B.
C. D.
7.某超市经销一种水果,每千克盈利10元,每天销售500千克,经市场调查反映:若每千克涨价1元,每天销售量减少20千克,设每千克涨价x (单位:元),且0≤x≤25,每天售出商品的利润为y (单位:元),则y与x的函数关系式是( )
A.y=500- 20x B.y=(500- 20x)(10+x)
C.y=(500+ 10x)(10-x) D.y=(500-10x)(10+x)
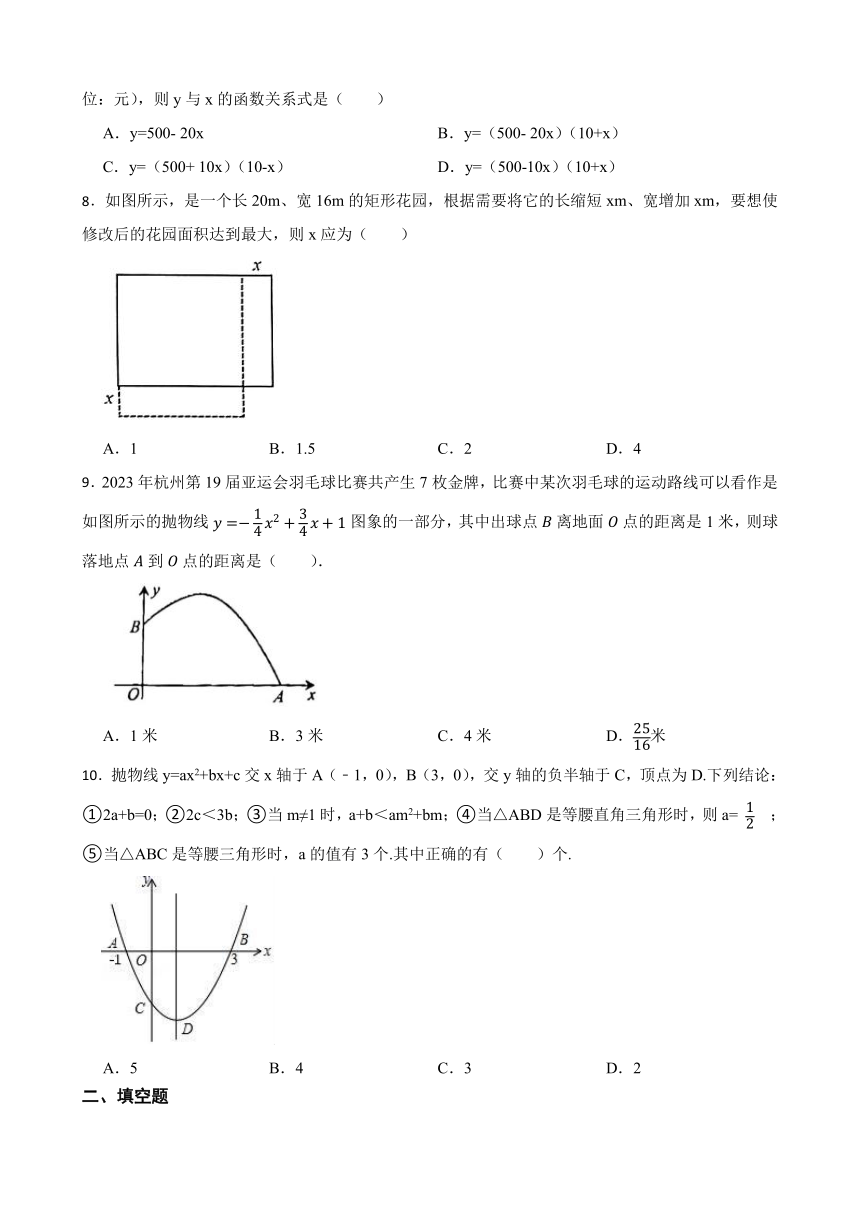
8.如图所示,是一个长20m、宽16m的矩形花园,根据需要将它的长缩短xm、宽增加xm,要想使修改后的花园面积达到最大,则x应为( )
A.1 B.1.5 C.2 D.4
9.2023年杭州第19届亚运会羽毛球比赛共产生7枚金牌,比赛中某次羽毛球的运动路线可以看作是如图所示的抛物线图象的一部分,其中出球点离地面点的距离是1米,则球落地点到点的距离是( ).
A.1米 B.3米 C.4米 D.米
10.抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a= ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
A.5 B.4 C.3 D.2
二、填空题
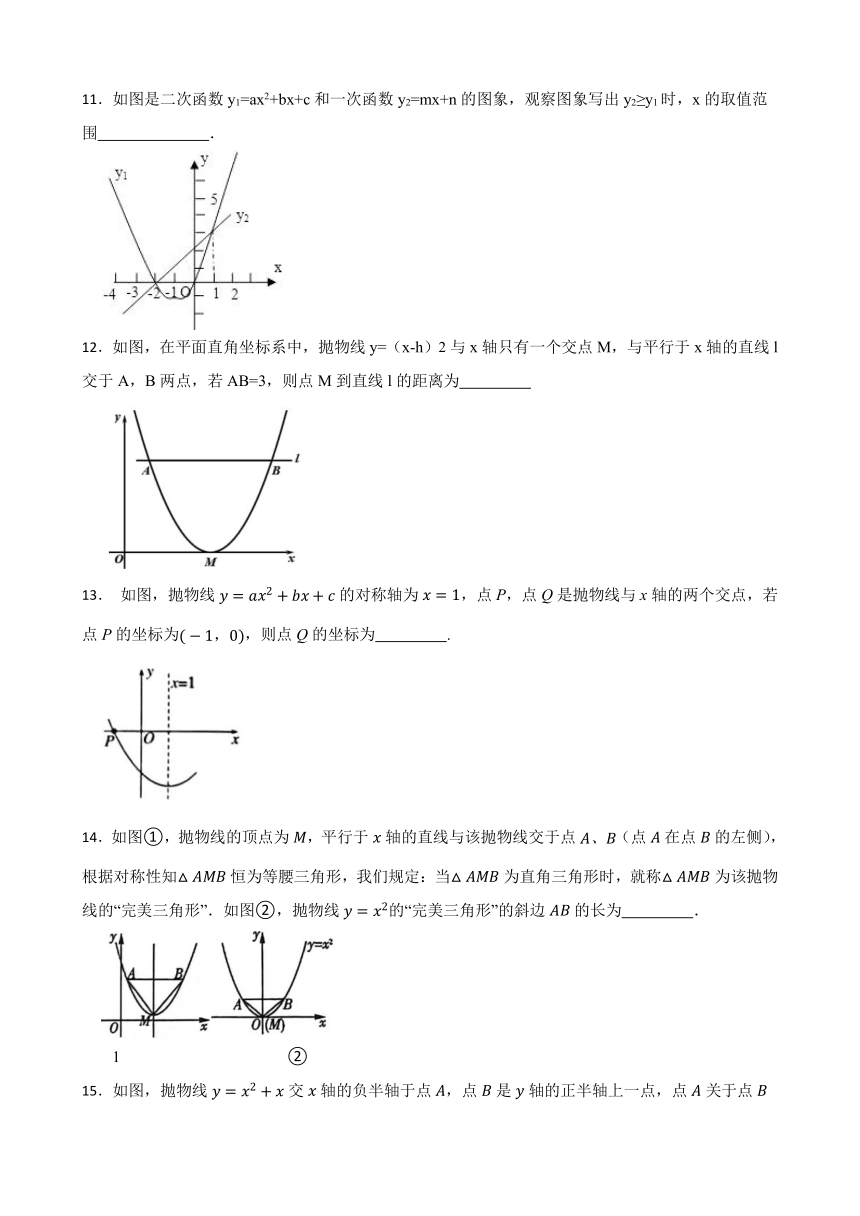
11.如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2≥y1时,x的取值范围 .
12.如图,在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点,若AB=3,则点M到直线l的距离为
13. 如图,抛物线的对称轴为,点P,点Q是抛物线与x轴的两个交点,若点P的坐标为,则点Q的坐标为 .
14.如图①,抛物线的顶点为,平行于轴的直线与该抛物线交于点(点在点的左侧),根据对称性知恒为等腰三角形,我们规定:当为直角三角形时,就称为该抛物线的“完美三角形”.如图②,抛物线的“完美三角形”的斜边的长为 .
1 ②
15.如图,抛物线交轴的负半轴于点,点是轴的正半轴上一点,点关于点的对称点恰好落在抛物线上.过点作轴的平行线交抛物线于另一点,则点的坐标为 .
16.已知抛物线,经过点.
(1)若时,,则此抛物线的对称轴为 ;
(2)当且时,都有,则的取值范围为 .
三、解答题
17.二次函数图象的顶点是,且经过点,求此函数的解析式.
18.已知抛物线与x轴交于点,其顶点记作点P.
(1)求此抛物线的顶点P的坐标.
(2)将抛物线向左平移m()个单位,使其顶点落在直线上,求平移后新抛物线的表达式.
19.如图,直线y=x+4与x轴,y轴分别交于点A,B.抛物线L:y=-x2+bx+3c经过点A,L与线段AB的另一个交点为点C(不与点B重合),P(m,n) 为抛物线上点A、C之间的一动点
(1)点A的坐标为 ,点B的坐标为
(2)求b,c的数量关系:
(3)若L经过OB的中点,
①求L的解析式:
②求点P到AB距离的最大值.
20.已知抛物线y=-(x-m)2+1与工轴的交点为A,B (点B在点A的右边),与y轴的交点为C.顶点为D.
(1)当m=1时,判断△ABD的形状,并说明理由.
(2)当点B在x轴的正半轴上,点C在轴的负半轴上时,是否存在某m值,使得△B0C为等腰三角形?若存在,求m的值;若不存在,请说明理由.
21.圆形喷水池中心O处有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点.已知雕塑料OA高米,与OA水平距离5米处为水柱最高点,落水点C、D之间的距高为22米,求喷出水柱的最大高度是多少米?
22.第31届世界大学生夏季运动会将于2023年7月28日至8月8日在成都举行,大熊猫是成都最具特色的对外传播标识物和“品牌图腾”,是天府之国享有极高知名度的个性名片.此次成都大运会吉祥物“蓉宝”(如图1)便是以熊猫基地真实的大熊猫“芝麻”为原型创作的.某商店销售“蓉宝”的公仔毛绒玩具,进价为30元/件,经市场调查发现:该商品的月销售量y(件)与销售价x(元/件)之间的关系如图2所示.
图1 图2
(1)求y关于x的函数解析式;
(2)由于某种原因,该商品进价提高了a元/件(),如果规定该玩具售价不超过40元/件,该商品在今后的销售中,月销售量与销售价仍然满足(1)中的函数关系,若该商品的月销售最大利润是2400元,求a的值.
答案解析部分
1.【答案】A
【解析】【解答】解:A:,是二次函数,符合题意;
B:,当a=0时,不是二次函数,不符合题意;
C:,是一次函数,不符合题意;
D:,不是二次函数,不符合题意;
故答案为:A。
【分析】用自变量的二次整式表示的函数是二次函数。
2.【答案】C
3.【答案】B
【解析】【解答】解:当 x=-4 时, ;
当 x=-3 时, ;
当 x=1 时, ,
所以 .
故答案为:B.
【分析】将A、B、C三边的横坐标分别代入解析式计算出y1、y2、y3的值,直接比较即可.
4.【答案】B
【解析】【解答】解:∵y=2x2+4x+5=2(x+1)2+3,
∴抛物线的开口向上,顶点坐标为(-1,3),
∴抛物线与坐标轴的交点个数为1个.
故答案为:B.
【分析】将抛物线的解析式配成顶点式,可得抛物线的开口向上,顶点坐标为(-1,3),在第二象限,从而即可得出抛物线与坐标轴交点的个数.
5.【答案】D
【解析】【解答】A选项:由一次函数图象知,a<0,b<0;由二次函数图象知,a>0,b>0,故A选项错误;
B选项:由一次函数图象知,a>0,b>0;由二次函数图象知,a<0,b<0,故B选项错误;
C选项:由一次函数图象知,a<0,b>0;由二次函数图象知,a>0,b>0,故C选项错误;
D选项:由一次函数图象知,a>0,b>0;由二次函数图象知,a>0,b>0,故D选项正确.
故本题应选D.
【分析】此类题一般是先假定其中的一个函数图象成立的基础上,读出其系数的取值范围,根据读出的条件再去判断同一坐标系中另一个函数图象是否正确即可。
6.【答案】B
【解析】【解答】解:根据表格中的对应值可知图象经过(3.24,-0.02)和(3.25,0.01),∴抛物线与X轴的一个交点在点(3.24,-0.02)和(3.25,0.01)之间,
∴关于x的方程的一个解x的范围是 3.24<x<3.25.
故答案为:B。
【分析】根据抛物线与x轴交点的纵坐标为0,介于-0.02和0.01之间,且抛物线与x轴交点的横坐标的值就是方程的解,即可得出答案。
7.【答案】B
【解析】【解答】解:当每千克涨价x元时,每千克盈利(10+x)元
每天可销售(500-20x)千克
由题意可得:y=(500-20x)(10+x)
故答案为:B
【分析】当每千克涨价x元时,每千克盈利(10+x)元,每天可销售(500-20x)千克,根据总利润=单件利润×总销售量即可求出答案.
8.【答案】C
9.【答案】C
【解析】【解答】解:∵抛物线解析式为,
∴将y=0代入,
可得:,
解得:x1=4,x2=-1,
∴点A的坐标为(4,0),
∴OA=4,
故答案为:C.
【分析】将y=0代入,可得求出x的值,可得点A的坐标,再求出AO的长即可.
10.【答案】C
【解析】【解答】解:①∵二次函数与x轴交于点A(-1,0)、B(3,0).
∴二次函数的对称轴为x= =1,即- =1,
∴2a+b=0.
故①正确;②∵二次函数y=ax2+bx+c与x轴交于点A(-1,0)、B(3,0).
∴a-b+c=0,9a+3b+c=0.
又∵b=-2a.
∴3b=-6a,a-(-2a)+c=0.
∴3b=-6a,2c=-6a.
∴2c=3b.
故②错误;③∵抛物线开口向上,对称轴是x=1.
∴x=1时,二次函数有最小值.
∴m≠1时,a+b+c<am2+bm+c.
即a+b<am2+bm.
故③正确;④∵AD=BD,AB=4,△ABD是等腰直角三角形.
∴AD2+BD2=42.
解得,AD2=8.
设点D坐标为(1,y).
则[1-(-1)]2+y2=AD2.
解得y=±2.
∵点D在x轴下方.
∴点D为(1,-2).
∵二次函数的顶点D为(1,-2),过点A(-1,0).
设二次函数解析式为y=a(x-1)2-2.
∴0=a(-1-1)2-2.
解得a= .
故④正确;⑤由图象可得,AC≠BC.
故△ABC是等腰三角形时,a的值有2个.
故⑤错误.
故①③④正确,②⑤错误.
故答案为:C.
【分析】根据二次函数图象与系数的关系,二次函数与x轴交于点A(-1,0)、B(3,0),可知二次函数的对称轴为x= =1,即- =1,可得2a与b的关系;将A、B两点代入可得c、b的关系;函数开口向下,x=1时取得最小值,则m≠1,可判断③;根据图象AD=BD,顶点坐标,判断④;由图象知BC≠AC,从而可以判断⑤.
11.【答案】﹣2≤x≤1
【解析】【解答】∵y1与y2的两交点横坐标为﹣2,1,
当y2≥y1时,y2的图象应在y1的图象上面,
即两图象交点之间的部分,
∴此时x的取值范围是﹣2≤x≤1.
【分析】观察函数图象,可知抛物线与x轴交点的横坐标分别为-2、1,要使y2≥y1时,就是一次函数的图象高于二次函数的图象,也就是两图像交点之间的部分,可求出x的取值范围。
12.【答案】
【解析】【解答】解:∵抛物线y=(x-h)2与x轴只有一个交点M,
∴点M的坐标为(h,0),对称轴为直线x=h,
∵抛物线与平行于x轴的直线l交于A,B两点,
∴点A、B的纵坐标相同,
设点A、B的纵坐标为m,
将y=m代入y=(x-h)2,可得:m=(x-h)2,
解得:m1=,m2=,
∴点A的坐标为(,m),点B的坐标为(,m),
∵AB=3,
∴-()=3,
解得:m=,
∴点M到直线l的距离为,
故答案为:.
【分析】设点A、B的纵坐标为m,将y=m代入y=(x-h)2,可得:m=(x-h)2,求出m的值,可得点A、B的坐标,再结合AB的长求出m的值,最后可得点M到直线l的距离为.
13.【答案】
14.【答案】2
15.【答案】
【解析】【解答】解:令y=0,则x2+x=0,x(x+1)=0,
∴A(-1,0),
∵点A关于点B的对称点A',
∴点A'的横坐标为1,
∵点A'在抛物线上,
∴y=2,
令函数值为2,得x2+x=2,
变形方程为:x2+x-2=0,
(x+2)(x-1)=0,
∴x1=-2,x2=1,
∴点C(-2,2),
故答案为:(-2,2).
【分析】先求出点A的坐标,再利用轴对称的性质求出点A'的坐标,再将y=2代入可得x2+x=2,再求出x的值,可得点C的坐标.
16.【答案】(1)2
(2)
【解析】【解答】解:(1)∵当时,,
∴点M、N关于对称轴对称,
∴抛物线的对称轴为:直线,
故答案为:直线x=2;
(2)①当m>0时,
∵当且时,都有,
∴0<2m≤4,
解得:0②当m<0时,
∵当且时,都有,
∴2m>4,
∴m>2(舍),
综上,m的取值范围为;
故答案为:.
【分析】(1)利用“点M、N关于对称轴对称”求出抛物线的对称轴为:直线;
(2)分类讨论:①当m>0时,②当m<0时,再分别列出不等式组求解即可.
17.【答案】解:设抛物线的解析式为,
将代入得,,
,
函数解析式为,
所以该抛物线的函数解析式为.
【解析】【分析】知道函数图象顶点坐标,直接设顶点式,再将B点坐标代入即可求出a.
18.【答案】(1)解:将点代入得
,
解得,
∴抛物线的表达式为,
∴此抛物线的顶点P的坐标为;
(2)解:由题意得平移后的抛物线的表达式为,
平移后的抛物线的顶点坐标为,
∵顶点落在直线上,
∴,
解得,
∴平移后新抛物线的表达式为.
【解析】【分析】(1)利用待定系数法求得抛物线的表达式,再配成顶点式,利用二次函数的性质求解;
(2)利用二次函数图象平移的性质:左加右减自变量,上加下减因变量,结合顶点在直线y=x上求解。
19.【答案】(1)(3, 0);(0, 4)
(2)解:把A(3,0)代入y= -x2+bx+3c得
-9+3b+3c= 0,
整理得b+c=3
(3)解:①由题知OB中点(0,2), 代入y= -x2+bx+3c得
3c=2,解得c=
又b+c=3,
∴b=
L的抛物线解析式为y=-x2+x+2.
②由题知,
解得或者
∴(,),
设P(m, -m2+m+ 2)(∵A(3,0), B(0, 4),
∴AB== 5,
连接BP,AP, OP,
∵S△PAB =S△PBO+S△PAO-S△OAB,
∴.
∴h=
∴当m=时,h的最大值时
∴点P到AB距离的最大值为
20.【答案】(1)解:将m=1代入y=-(x-m)2+1得y=-(x-1)2+1 ,
∴点D(1,1),
令y=0,得-(x-1)2+1=0,
解得x=0或x=2,
∴A(0,0),B(2,0),
∴AD2=(1-0)2+(1-0)2=2,BD2=(1-2)2+(1-0)2=2,AB2=4,
∴AD=BD,且AD2+BD2=AB2,
∴△ABD是等腰直角三角形;
(2)解:存在某个m的值,使得△BOC是等腰直角三角形,理由如下:
当y=0时, -(x-m)2+1=0,
解得x=m-1或x=m+1,
∴A(m-1,0),B(m+1,0),
∵点B在x轴的正半轴上 ,
∴OB=m+1,
当x=0时,y=1-m2,
∴点C(0,1-m2),
又点C在y轴的负半轴上,
∴OC=m2-1,
由△BOC是等腰三角形,得OB=OC,
∴m2-1=m+1,
解得m1=2,m2=-1,
∵m+1>0,
∴ m=2,
∴△BOC是等腰直角三角形时,m的值为2.
【解析】【分析】(1)将m=1代入y=-(x-m)2+1可得抛物线的顶点式,则顶点D(1,1),令解析式中的y=0,求解得出x的值,从而可得点A、B的坐标,根据两点间的距离公式及勾股定理的逆定理判断出△ABD是等腰直角三角形;
(2)令抛物线解析式中的y=0,算出对应的x的值可得点A、B的坐标,进而根据点B在x轴的正半轴上 ,可表示出OB的长;令抛物线解析式中的x=0,算出对应的y的值可得点C的坐标,进而根据点C在y轴的负半轴上 ,可表示出OC的长;由△BOC是等腰三角形,得OB=OC,据此建立方程求解可得m的值,求解可得答案.
21.【答案】解:由题知,水柱形成抛物线的对称轴为直线x=5,A(0,),D(11, 0),
设抛物线解析式为y=a(x- 5)2+k, 把A(0,),D(11, 0)代入,得
解得
∴水柱形成抛物线的解析式为y= (x-5)2+ 6,
∴拋物线顶点坐标为(5, 6),
∴喷出水柱的最大高度是6米.
22.【答案】(1)解:设y关于x的函数解析式为,
由题意得解得,
∴y关于x的函数解析式为;
(2)解:由题意得,利润,
对称轴为直线,∵,∴,
∵规定该玩具售价不超过40元/件,∴时,ω取最大值2400,
∴,解得a=2.
【解析】【分析】(1)设关于x的函数表达式为y=kx+b,在图象上找到两个点的坐标,用待定系数法求解;
(2)根据总利润=(售价-进价)数量建立总利润的二次函数,根据二次函数的性质求解。
一、选择题
1.下列函数解析式中,一定为二次函数的是( )
A. B. C. D.
2.格二次函数y=2x2+4x-6化成y=a(x-h)2+k的形式为( )
A.y=2(x-1)2+8 B.y= 2(x+1)2-4
C.y=2(x+1)2-8 D.y=2(x+2)2-10
3.若 , , 为二次函数 的图象上的三点,则 , , 的大小关系是 .
A. B. C. D.
4.抛物线y=2x2+4x +5与坐标轴的交点个数为( )
(A) (B) (C) (D)
A.0个 B.1个 C.2个 D.3个
5.在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )
A. B.
C. D.
6. 根据下列表格对应值:
判断关于x的方程的一个解x的范围是( )
A. B.
C. D.
7.某超市经销一种水果,每千克盈利10元,每天销售500千克,经市场调查反映:若每千克涨价1元,每天销售量减少20千克,设每千克涨价x (单位:元),且0≤x≤25,每天售出商品的利润为y (单位:元),则y与x的函数关系式是( )
A.y=500- 20x B.y=(500- 20x)(10+x)
C.y=(500+ 10x)(10-x) D.y=(500-10x)(10+x)
8.如图所示,是一个长20m、宽16m的矩形花园,根据需要将它的长缩短xm、宽增加xm,要想使修改后的花园面积达到最大,则x应为( )
A.1 B.1.5 C.2 D.4
9.2023年杭州第19届亚运会羽毛球比赛共产生7枚金牌,比赛中某次羽毛球的运动路线可以看作是如图所示的抛物线图象的一部分,其中出球点离地面点的距离是1米,则球落地点到点的距离是( ).
A.1米 B.3米 C.4米 D.米
10.抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a= ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
A.5 B.4 C.3 D.2
二、填空题
11.如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2≥y1时,x的取值范围 .
12.如图,在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点,若AB=3,则点M到直线l的距离为
13. 如图,抛物线的对称轴为,点P,点Q是抛物线与x轴的两个交点,若点P的坐标为,则点Q的坐标为 .
14.如图①,抛物线的顶点为,平行于轴的直线与该抛物线交于点(点在点的左侧),根据对称性知恒为等腰三角形,我们规定:当为直角三角形时,就称为该抛物线的“完美三角形”.如图②,抛物线的“完美三角形”的斜边的长为 .
1 ②
15.如图,抛物线交轴的负半轴于点,点是轴的正半轴上一点,点关于点的对称点恰好落在抛物线上.过点作轴的平行线交抛物线于另一点,则点的坐标为 .
16.已知抛物线,经过点.
(1)若时,,则此抛物线的对称轴为 ;
(2)当且时,都有,则的取值范围为 .
三、解答题
17.二次函数图象的顶点是,且经过点,求此函数的解析式.
18.已知抛物线与x轴交于点,其顶点记作点P.
(1)求此抛物线的顶点P的坐标.
(2)将抛物线向左平移m()个单位,使其顶点落在直线上,求平移后新抛物线的表达式.
19.如图,直线y=x+4与x轴,y轴分别交于点A,B.抛物线L:y=-x2+bx+3c经过点A,L与线段AB的另一个交点为点C(不与点B重合),P(m,n) 为抛物线上点A、C之间的一动点
(1)点A的坐标为 ,点B的坐标为
(2)求b,c的数量关系:
(3)若L经过OB的中点,
①求L的解析式:
②求点P到AB距离的最大值.
20.已知抛物线y=-(x-m)2+1与工轴的交点为A,B (点B在点A的右边),与y轴的交点为C.顶点为D.
(1)当m=1时,判断△ABD的形状,并说明理由.
(2)当点B在x轴的正半轴上,点C在轴的负半轴上时,是否存在某m值,使得△B0C为等腰三角形?若存在,求m的值;若不存在,请说明理由.
21.圆形喷水池中心O处有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立平面直角坐标系,点A在y轴上,x轴上的点C、D为水柱的落水点.已知雕塑料OA高米,与OA水平距离5米处为水柱最高点,落水点C、D之间的距高为22米,求喷出水柱的最大高度是多少米?
22.第31届世界大学生夏季运动会将于2023年7月28日至8月8日在成都举行,大熊猫是成都最具特色的对外传播标识物和“品牌图腾”,是天府之国享有极高知名度的个性名片.此次成都大运会吉祥物“蓉宝”(如图1)便是以熊猫基地真实的大熊猫“芝麻”为原型创作的.某商店销售“蓉宝”的公仔毛绒玩具,进价为30元/件,经市场调查发现:该商品的月销售量y(件)与销售价x(元/件)之间的关系如图2所示.
图1 图2
(1)求y关于x的函数解析式;
(2)由于某种原因,该商品进价提高了a元/件(),如果规定该玩具售价不超过40元/件,该商品在今后的销售中,月销售量与销售价仍然满足(1)中的函数关系,若该商品的月销售最大利润是2400元,求a的值.
答案解析部分
1.【答案】A
【解析】【解答】解:A:,是二次函数,符合题意;
B:,当a=0时,不是二次函数,不符合题意;
C:,是一次函数,不符合题意;
D:,不是二次函数,不符合题意;
故答案为:A。
【分析】用自变量的二次整式表示的函数是二次函数。
2.【答案】C
3.【答案】B
【解析】【解答】解:当 x=-4 时, ;
当 x=-3 时, ;
当 x=1 时, ,
所以 .
故答案为:B.
【分析】将A、B、C三边的横坐标分别代入解析式计算出y1、y2、y3的值,直接比较即可.
4.【答案】B
【解析】【解答】解:∵y=2x2+4x+5=2(x+1)2+3,
∴抛物线的开口向上,顶点坐标为(-1,3),
∴抛物线与坐标轴的交点个数为1个.
故答案为:B.
【分析】将抛物线的解析式配成顶点式,可得抛物线的开口向上,顶点坐标为(-1,3),在第二象限,从而即可得出抛物线与坐标轴交点的个数.
5.【答案】D
【解析】【解答】A选项:由一次函数图象知,a<0,b<0;由二次函数图象知,a>0,b>0,故A选项错误;
B选项:由一次函数图象知,a>0,b>0;由二次函数图象知,a<0,b<0,故B选项错误;
C选项:由一次函数图象知,a<0,b>0;由二次函数图象知,a>0,b>0,故C选项错误;
D选项:由一次函数图象知,a>0,b>0;由二次函数图象知,a>0,b>0,故D选项正确.
故本题应选D.
【分析】此类题一般是先假定其中的一个函数图象成立的基础上,读出其系数的取值范围,根据读出的条件再去判断同一坐标系中另一个函数图象是否正确即可。
6.【答案】B
【解析】【解答】解:根据表格中的对应值可知图象经过(3.24,-0.02)和(3.25,0.01),∴抛物线与X轴的一个交点在点(3.24,-0.02)和(3.25,0.01)之间,
∴关于x的方程的一个解x的范围是 3.24<x<3.25.
故答案为:B。
【分析】根据抛物线与x轴交点的纵坐标为0,介于-0.02和0.01之间,且抛物线与x轴交点的横坐标的值就是方程的解,即可得出答案。
7.【答案】B
【解析】【解答】解:当每千克涨价x元时,每千克盈利(10+x)元
每天可销售(500-20x)千克
由题意可得:y=(500-20x)(10+x)
故答案为:B
【分析】当每千克涨价x元时,每千克盈利(10+x)元,每天可销售(500-20x)千克,根据总利润=单件利润×总销售量即可求出答案.
8.【答案】C
9.【答案】C
【解析】【解答】解:∵抛物线解析式为,
∴将y=0代入,
可得:,
解得:x1=4,x2=-1,
∴点A的坐标为(4,0),
∴OA=4,
故答案为:C.
【分析】将y=0代入,可得求出x的值,可得点A的坐标,再求出AO的长即可.
10.【答案】C
【解析】【解答】解:①∵二次函数与x轴交于点A(-1,0)、B(3,0).
∴二次函数的对称轴为x= =1,即- =1,
∴2a+b=0.
故①正确;②∵二次函数y=ax2+bx+c与x轴交于点A(-1,0)、B(3,0).
∴a-b+c=0,9a+3b+c=0.
又∵b=-2a.
∴3b=-6a,a-(-2a)+c=0.
∴3b=-6a,2c=-6a.
∴2c=3b.
故②错误;③∵抛物线开口向上,对称轴是x=1.
∴x=1时,二次函数有最小值.
∴m≠1时,a+b+c<am2+bm+c.
即a+b<am2+bm.
故③正确;④∵AD=BD,AB=4,△ABD是等腰直角三角形.
∴AD2+BD2=42.
解得,AD2=8.
设点D坐标为(1,y).
则[1-(-1)]2+y2=AD2.
解得y=±2.
∵点D在x轴下方.
∴点D为(1,-2).
∵二次函数的顶点D为(1,-2),过点A(-1,0).
设二次函数解析式为y=a(x-1)2-2.
∴0=a(-1-1)2-2.
解得a= .
故④正确;⑤由图象可得,AC≠BC.
故△ABC是等腰三角形时,a的值有2个.
故⑤错误.
故①③④正确,②⑤错误.
故答案为:C.
【分析】根据二次函数图象与系数的关系,二次函数与x轴交于点A(-1,0)、B(3,0),可知二次函数的对称轴为x= =1,即- =1,可得2a与b的关系;将A、B两点代入可得c、b的关系;函数开口向下,x=1时取得最小值,则m≠1,可判断③;根据图象AD=BD,顶点坐标,判断④;由图象知BC≠AC,从而可以判断⑤.
11.【答案】﹣2≤x≤1
【解析】【解答】∵y1与y2的两交点横坐标为﹣2,1,
当y2≥y1时,y2的图象应在y1的图象上面,
即两图象交点之间的部分,
∴此时x的取值范围是﹣2≤x≤1.
【分析】观察函数图象,可知抛物线与x轴交点的横坐标分别为-2、1,要使y2≥y1时,就是一次函数的图象高于二次函数的图象,也就是两图像交点之间的部分,可求出x的取值范围。
12.【答案】
【解析】【解答】解:∵抛物线y=(x-h)2与x轴只有一个交点M,
∴点M的坐标为(h,0),对称轴为直线x=h,
∵抛物线与平行于x轴的直线l交于A,B两点,
∴点A、B的纵坐标相同,
设点A、B的纵坐标为m,
将y=m代入y=(x-h)2,可得:m=(x-h)2,
解得:m1=,m2=,
∴点A的坐标为(,m),点B的坐标为(,m),
∵AB=3,
∴-()=3,
解得:m=,
∴点M到直线l的距离为,
故答案为:.
【分析】设点A、B的纵坐标为m,将y=m代入y=(x-h)2,可得:m=(x-h)2,求出m的值,可得点A、B的坐标,再结合AB的长求出m的值,最后可得点M到直线l的距离为.
13.【答案】
14.【答案】2
15.【答案】
【解析】【解答】解:令y=0,则x2+x=0,x(x+1)=0,
∴A(-1,0),
∵点A关于点B的对称点A',
∴点A'的横坐标为1,
∵点A'在抛物线上,
∴y=2,
令函数值为2,得x2+x=2,
变形方程为:x2+x-2=0,
(x+2)(x-1)=0,
∴x1=-2,x2=1,
∴点C(-2,2),
故答案为:(-2,2).
【分析】先求出点A的坐标,再利用轴对称的性质求出点A'的坐标,再将y=2代入可得x2+x=2,再求出x的值,可得点C的坐标.
16.【答案】(1)2
(2)
【解析】【解答】解:(1)∵当时,,
∴点M、N关于对称轴对称,
∴抛物线的对称轴为:直线,
故答案为:直线x=2;
(2)①当m>0时,
∵当且时,都有,
∴0<2m≤4,
解得:0
∵当且时,都有,
∴2m>4,
∴m>2(舍),
综上,m的取值范围为;
故答案为:.
【分析】(1)利用“点M、N关于对称轴对称”求出抛物线的对称轴为:直线;
(2)分类讨论:①当m>0时,②当m<0时,再分别列出不等式组求解即可.
17.【答案】解:设抛物线的解析式为,
将代入得,,
,
函数解析式为,
所以该抛物线的函数解析式为.
【解析】【分析】知道函数图象顶点坐标,直接设顶点式,再将B点坐标代入即可求出a.
18.【答案】(1)解:将点代入得
,
解得,
∴抛物线的表达式为,
∴此抛物线的顶点P的坐标为;
(2)解:由题意得平移后的抛物线的表达式为,
平移后的抛物线的顶点坐标为,
∵顶点落在直线上,
∴,
解得,
∴平移后新抛物线的表达式为.
【解析】【分析】(1)利用待定系数法求得抛物线的表达式,再配成顶点式,利用二次函数的性质求解;
(2)利用二次函数图象平移的性质:左加右减自变量,上加下减因变量,结合顶点在直线y=x上求解。
19.【答案】(1)(3, 0);(0, 4)
(2)解:把A(3,0)代入y= -x2+bx+3c得
-9+3b+3c= 0,
整理得b+c=3
(3)解:①由题知OB中点(0,2), 代入y= -x2+bx+3c得
3c=2,解得c=
又b+c=3,
∴b=
L的抛物线解析式为y=-x2+x+2.
②由题知,
解得或者
∴(,),
设P(m, -m2+m+ 2)(
∴AB== 5,
连接BP,AP, OP,
∵S△PAB =S△PBO+S△PAO-S△OAB,
∴.
∴h=
∴当m=时,h的最大值时
∴点P到AB距离的最大值为
20.【答案】(1)解:将m=1代入y=-(x-m)2+1得y=-(x-1)2+1 ,
∴点D(1,1),
令y=0,得-(x-1)2+1=0,
解得x=0或x=2,
∴A(0,0),B(2,0),
∴AD2=(1-0)2+(1-0)2=2,BD2=(1-2)2+(1-0)2=2,AB2=4,
∴AD=BD,且AD2+BD2=AB2,
∴△ABD是等腰直角三角形;
(2)解:存在某个m的值,使得△BOC是等腰直角三角形,理由如下:
当y=0时, -(x-m)2+1=0,
解得x=m-1或x=m+1,
∴A(m-1,0),B(m+1,0),
∵点B在x轴的正半轴上 ,
∴OB=m+1,
当x=0时,y=1-m2,
∴点C(0,1-m2),
又点C在y轴的负半轴上,
∴OC=m2-1,
由△BOC是等腰三角形,得OB=OC,
∴m2-1=m+1,
解得m1=2,m2=-1,
∵m+1>0,
∴ m=2,
∴△BOC是等腰直角三角形时,m的值为2.
【解析】【分析】(1)将m=1代入y=-(x-m)2+1可得抛物线的顶点式,则顶点D(1,1),令解析式中的y=0,求解得出x的值,从而可得点A、B的坐标,根据两点间的距离公式及勾股定理的逆定理判断出△ABD是等腰直角三角形;
(2)令抛物线解析式中的y=0,算出对应的x的值可得点A、B的坐标,进而根据点B在x轴的正半轴上 ,可表示出OB的长;令抛物线解析式中的x=0,算出对应的y的值可得点C的坐标,进而根据点C在y轴的负半轴上 ,可表示出OC的长;由△BOC是等腰三角形,得OB=OC,据此建立方程求解可得m的值,求解可得答案.
21.【答案】解:由题知,水柱形成抛物线的对称轴为直线x=5,A(0,),D(11, 0),
设抛物线解析式为y=a(x- 5)2+k, 把A(0,),D(11, 0)代入,得
解得
∴水柱形成抛物线的解析式为y= (x-5)2+ 6,
∴拋物线顶点坐标为(5, 6),
∴喷出水柱的最大高度是6米.
22.【答案】(1)解:设y关于x的函数解析式为,
由题意得解得,
∴y关于x的函数解析式为;
(2)解:由题意得,利润,
对称轴为直线,∵,∴,
∵规定该玩具售价不超过40元/件,∴时,ω取最大值2400,
∴,解得a=2.
【解析】【分析】(1)设关于x的函数表达式为y=kx+b,在图象上找到两个点的坐标,用待定系数法求解;
(2)根据总利润=(售价-进价)数量建立总利润的二次函数,根据二次函数的性质求解。
同课章节目录
