浙江省乐清市育英寄宿学校浙教版八年级数学下册课件:51矩形(2)(共20张PPT)
文档属性
| 名称 | 浙江省乐清市育英寄宿学校浙教版八年级数学下册课件:51矩形(2)(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 563.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-14 11:44:34 | ||
图片预览







文档简介
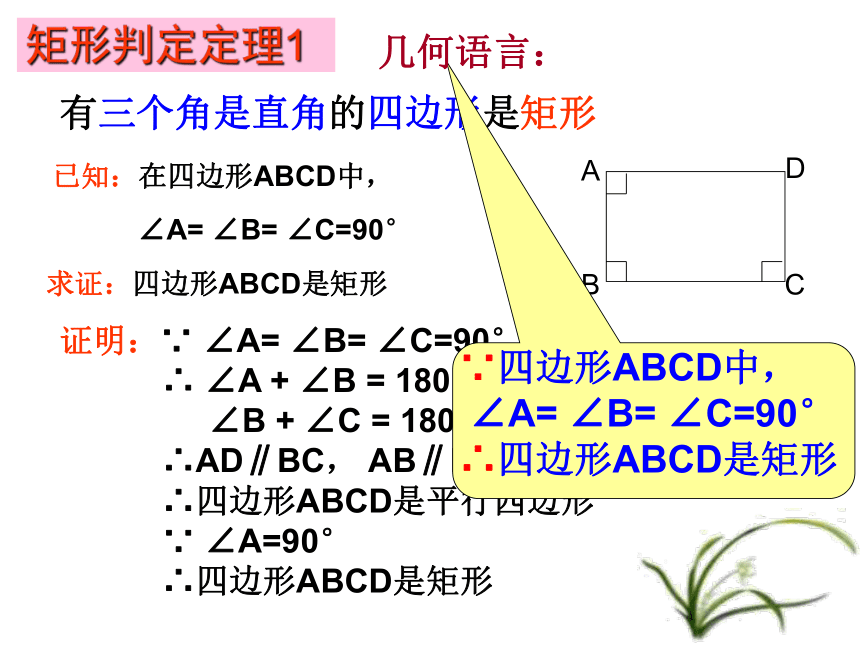
课件20张PPT。 温故而知新定义:有一个角是直角的平行四边形叫做矩形四个角都是直角对边平行且相等互相平分且相等中心对称图形,轴对称图形5.1矩形(2) 小明家出现了一件麻烦事:因为家里的铝合金窗关不严,每当下雨的时候铝合金窗老是漏雨.妈妈想是不是窗户的形状有问题呢?他从家里找来卷尺和直角尺就……聪明的同学们,你们知道小明的办法是什么吗?有一个角是直角的平行四边形叫做矩形 (1)测量两组对边,发现两组对边分别相等(2)将直角尺靠紧窗框的一个角,测得这是直角由此说明这个窗框是矩形你知道这是为什么吗?小明的方法如下: 小明家出现了一件麻烦事:因为家里的铝合金窗关不严,每当下雨的时候铝合金窗老是漏雨.妈妈想是不是窗户的形状有问题呢?若现在家里只能找到一把直角尺你能帮小明想想办法吗?方法如下:将直角尺依次靠紧窗框的每一个角,测得这四个角都是直角.由此说明这个窗框是矩形这种方法可行吗?为什么?(用所学的知识去证明)你对上述方法有什么想法吗?请你思考—要判定一个四边形是矩形只要说明几个角是直角?为什么?我们已经知道矩形的四个角都是直角,由此你想到了什么方法呢?有三个角是直角的四边形是矩形证明:∵ ∠A= ∠B= ∠C=90°
∴ ∠A + ∠B = 180°
∠B + ∠C = 180°
∴AD∥BC, AB∥DC
∴四边形ABCD是平行四边形
∵ ∠A=90°
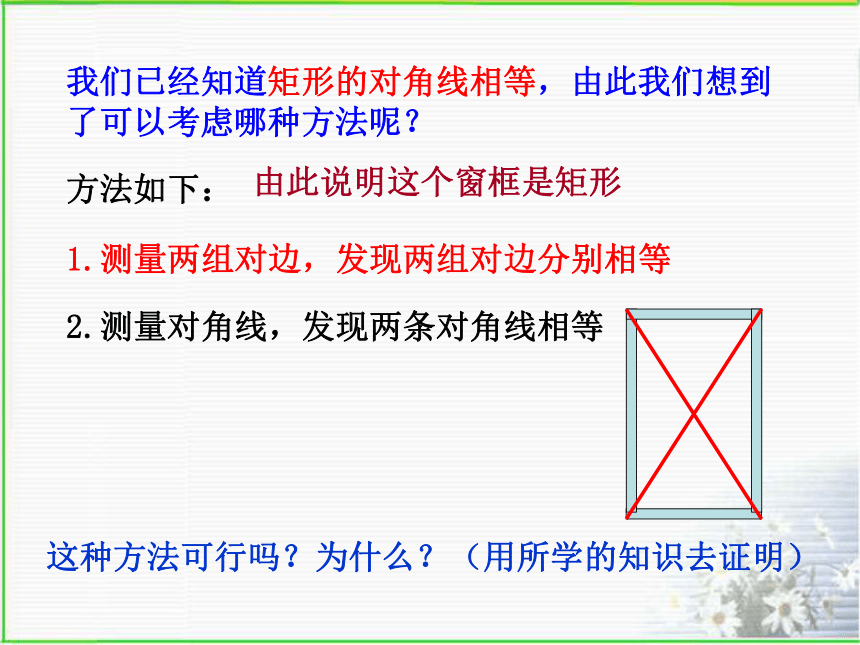
∴四边形ABCD是矩形矩形判定定理1几何语言: 小明家出现了一件麻烦事:因为家里的铝合金窗关不严,每当下雨的时候铝合金窗老是漏雨.妈妈想是不是窗户的形状有问题呢?若现在家里只能找到一把卷尺你能帮小明想想办法吗?这种方法可行吗?为什么?(用所学的知识去证明)我们已经知道矩形的对角线相等,由此我们想到了可以考虑哪种方法呢?1.测量两组对边,发现两组对边分别相等2.测量对角线,发现两条对角线相等方法如下:由此说明这个窗框是矩形对角线相等的平行四边形是矩形。已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。证明:在平行四边形ABCD中 ,AB=CD
∵BC=BC
AC=BD∴ △ABC≌ △DCB(SSS)∵ AB//CD
∴ ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形∴四边形ABCD是矩形∴ ∠ABC=∠DCB判定定理2几何语言:
∵在□ABCD中, AC=BD
∴□ABCD是矩形平行四边形是矩形.四边形是矩形.矩形的判定方法:利用上图:判断下列命题是否正确,并说明理由。 (1)对角互补的平行四边形是矩形。(2)一组邻角相等的平行四边形是矩形。(3)对角线相等的四边形是矩形。(4)内角都相等的四边形是矩形。ABCD注意审题哦!火眼金睛辩是非正确正确错误正确[例题]一张四边形纸板ABCD形状如图,
(1)若要在这张纸板中画一个平行四边形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可怎样画?EFGH⑵四边形ABCD满足什么条件时,四边形EFGH为矩形?并说明理由.解:分别取AB,BC,CD,DA的中点E,F,G,H,连接可得四边形EFGH为平行四边形.两条对角线互相垂直,AC⊥BD解:一张四边形纸板ABCD满足____________时
分别取AB,BC,CD,DA的中点E,F,G,H,就能画出
中点四边形EFGH是矩形,EFGH理由如下:∵GH是△ACD的中位线∴GH∥AC123∵AC⊥BD∴∠1=90°(三角形的中位线平行于第三边
且等于第三边的一半)∴∠2=∠1=90°∵EH是△ABD的中位线∴EH∥BD∴∠3=∠2=90°,45(三角形的中位线平行于第三边)同理可得:∠4=90°, ∠5=90°∴四边形EFGH是矩形.(三个角是直角的四边形是矩形)两条对角线互相垂直 如图,AC、BD是矩形ABCD的两条对角线,AE=CG=BF=DH.求证:四边形EFGH是矩形.大显身手证明: 在矩形ABCD中, AC=BD ,
AO=CO=BO=DO∵AE=CG=BF=DH ∴ OE=OG=OF=OH, EG=FH ∴四边形EFGH是平行四边形∴四边形EFGH是矩形这节课你有什么收获啊?回头看收获!还有哪些疑问呢?任意一个四边形,
三个直角定矩形。
对于平行四边形,
一个直角即可定;
对线相等也矩形。矩形的判定口诀:如图, 在平行四边形ABCD中,AF,BH,CH,DF分别
平分∠BAD, ∠ABC, ∠BCD, ∠ADC,
求证:EG=HF.ABCDHEFG挑战无处不在 如图,在四边形ABCD中,AB=AD,CB=CD,点M,N,P,Q分别是AB,BC,CD,DA的中点.
求证:四边形MNPQ是矩形.拓展延伸作业:《作业本1》
∴ ∠A + ∠B = 180°
∠B + ∠C = 180°
∴AD∥BC, AB∥DC
∴四边形ABCD是平行四边形
∵ ∠A=90°
∴四边形ABCD是矩形矩形判定定理1几何语言: 小明家出现了一件麻烦事:因为家里的铝合金窗关不严,每当下雨的时候铝合金窗老是漏雨.妈妈想是不是窗户的形状有问题呢?若现在家里只能找到一把卷尺你能帮小明想想办法吗?这种方法可行吗?为什么?(用所学的知识去证明)我们已经知道矩形的对角线相等,由此我们想到了可以考虑哪种方法呢?1.测量两组对边,发现两组对边分别相等2.测量对角线,发现两条对角线相等方法如下:由此说明这个窗框是矩形对角线相等的平行四边形是矩形。已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。证明:在平行四边形ABCD中 ,AB=CD
∵BC=BC
AC=BD∴ △ABC≌ △DCB(SSS)∵ AB//CD
∴ ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形∴四边形ABCD是矩形∴ ∠ABC=∠DCB判定定理2几何语言:
∵在□ABCD中, AC=BD
∴□ABCD是矩形平行四边形是矩形.四边形是矩形.矩形的判定方法:利用上图:判断下列命题是否正确,并说明理由。 (1)对角互补的平行四边形是矩形。(2)一组邻角相等的平行四边形是矩形。(3)对角线相等的四边形是矩形。(4)内角都相等的四边形是矩形。ABCD注意审题哦!火眼金睛辩是非正确正确错误正确[例题]一张四边形纸板ABCD形状如图,
(1)若要在这张纸板中画一个平行四边形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可怎样画?EFGH⑵四边形ABCD满足什么条件时,四边形EFGH为矩形?并说明理由.解:分别取AB,BC,CD,DA的中点E,F,G,H,连接可得四边形EFGH为平行四边形.两条对角线互相垂直,AC⊥BD解:一张四边形纸板ABCD满足____________时
分别取AB,BC,CD,DA的中点E,F,G,H,就能画出
中点四边形EFGH是矩形,EFGH理由如下:∵GH是△ACD的中位线∴GH∥AC123∵AC⊥BD∴∠1=90°(三角形的中位线平行于第三边
且等于第三边的一半)∴∠2=∠1=90°∵EH是△ABD的中位线∴EH∥BD∴∠3=∠2=90°,45(三角形的中位线平行于第三边)同理可得:∠4=90°, ∠5=90°∴四边形EFGH是矩形.(三个角是直角的四边形是矩形)两条对角线互相垂直 如图,AC、BD是矩形ABCD的两条对角线,AE=CG=BF=DH.求证:四边形EFGH是矩形.大显身手证明: 在矩形ABCD中, AC=BD ,
AO=CO=BO=DO∵AE=CG=BF=DH ∴ OE=OG=OF=OH, EG=FH ∴四边形EFGH是平行四边形∴四边形EFGH是矩形这节课你有什么收获啊?回头看收获!还有哪些疑问呢?任意一个四边形,
三个直角定矩形。
对于平行四边形,
一个直角即可定;
对线相等也矩形。矩形的判定口诀:如图, 在平行四边形ABCD中,AF,BH,CH,DF分别
平分∠BAD, ∠ABC, ∠BCD, ∠ADC,
求证:EG=HF.ABCDHEFG挑战无处不在 如图,在四边形ABCD中,AB=AD,CB=CD,点M,N,P,Q分别是AB,BC,CD,DA的中点.
求证:四边形MNPQ是矩形.拓展延伸作业:《作业本1》
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
