7.6余角和补角说课课件(浙江省杭州市富阳市)
文档属性
| 名称 | 7.6余角和补角说课课件(浙江省杭州市富阳市) |
|
|
| 格式 | rar | ||
| 文件大小 | 120.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-26 15:03:00 | ||
图片预览









文档简介
课件30张PPT。7.6余角和补角.浙教版设计板块地位与作用余角和补角是《图形的初步知识》的重要组成部分,互余和互补既是图形关系,也是一种数量关系。
《图形的初步知识》这一章节是学生平面几何的基础的入门课.作为实验几何向论证几何过渡的重要过程,为以后论证角的相等也打下了良好的基础,也为培养和发展学生的逻辑思维能力、观察分析能力、演绎归纳能力打下了结实的基础。教材分析知识目标 理解余角和补角的概念,掌握余角和补角的概念及性质,并能运用它们解决一些实际问题。能力目标情感目标 经历观察、操作、推理、交流等活动,发展学生的几何概念,初步培养学生的几何推理与表达的能力。能运用方程思想解决几何问题 体验数学知识的发生、发展过程,敢于面对数学活动中的困难,建立学好数学的自信心。教学目标教材分析教学重点:余角和补角的性质应用常常需要 几何说理,或综合运用代数知识,特别是用代数的方法来计算角的度数要求较高.教学难点:余角和补角的概念和性质。教材分析 知识基础上说小学里已经初步接触,本节课是在认识直角、平角的基础上,比较角的大小后,通过数量关系和图形关系学习两角互余、互补的概念和性质。学情分析 本课许多知识的构成与现实生活紧密相连,如方位角等能够吸引学生的注意力,利于培养学生学习数学的兴趣。初一学生逻辑思维能力,抽象能力,几何表达能力都还较弱。必须借助于形象思维。采用多媒体辅助教学,增强图形的动感效应,生动形象的表达图形的变化过程,提高教学效果。教法与学法加强直观教学,感性教学把教学过程转化为观察、发现、动手模仿的过程,提高学生学习的兴趣,增强信心。教法: 学法: 通过模仿、操作学会观察、分析,从具体实例中抽象出数学知识以及一般性的结论的思想方法,运用类比思想和方程思想理解与解决问题。
情景引入(图片)直角纸片的剪与拼得出概念(类比)巩固概念题组训练1(图形语言描述)余、补角的性质(类比总结)例1. 说理(模仿)例2.综合运用(方程思想)题组2小节拓展提高教学流程设计教学过程(方位角)海塘大坝要修复加固,施工前要求先测出大坝的倾斜角(即图中的∠1),坝底是石块堆积而成,量角器无法伸入大坝底部测量,聪明的你有什么简单的方法?想一想教学过程情景引入1. 如图,在你手边直角内任画一条射线把直角分成两部分两部分∠1 和∠2。2. 量出∠1 和∠2的度数并标在角内部.把它们剪开.
动一动,拼一拼教学过程3. 把你所剪的角与旁边的同学所剪的拼一拼能拼出直角吗? 4. 想一想如果两个角要拼成直角,它们的度数有什么要求?教学过程如果两个角的和是直角,就说这两个角 互为余角 (complementary angle) 简称“互余”图形上认识若∠1与∠2能拼成直角,则 ∠1与∠2互余。数量上认识若∠1+∠2 =90°,则 ∠1与∠2互余。
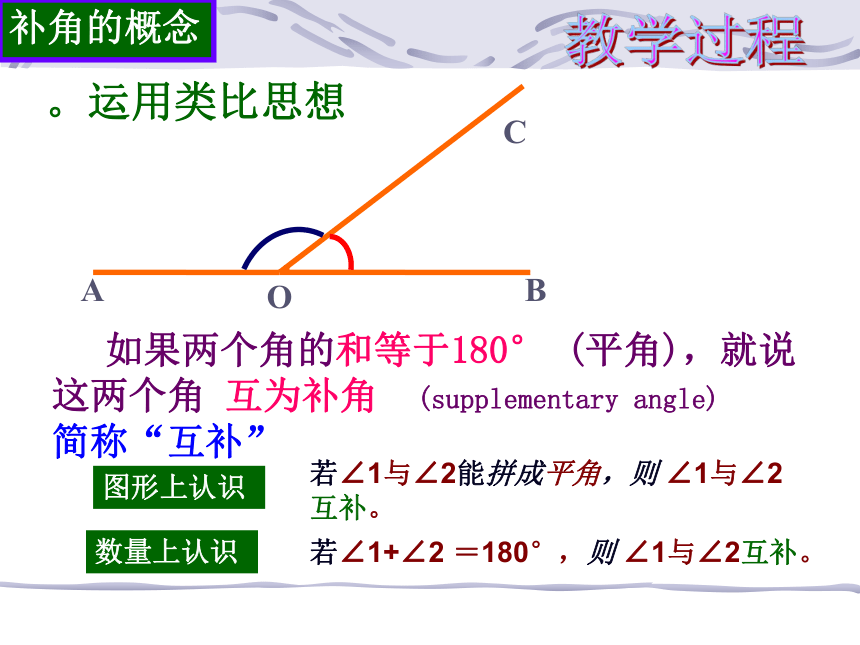
余角的概念ABCO教学过程 如果两个角的和等于180° (平角),就说这两个角 互为补角 (supplementary angle) 简称“互补”。运用类比思想图形上认识若∠1与∠2能拼成平角,则 ∠1与∠2互补。数量上认识若∠1+∠2 =180°,则 ∠1与∠2互补。
补角的概念1.读一读.理一理
如果 的和是一个 ,那么这两个角叫做 余角,其中一个角是 的余角。
如果 的和是一个 ,那么这两个角叫做 补角,其中一个角是 的补角。
两个角直角互为另一个角两个角互为 另一个角平角教学过程题组一.强化概念2.找朋友:图中给出的各角中,哪些互为余角?哪些互为补角?(注意解题方法指导)°°°°°°°°题组一.强化概念教学过程3.仔细观察,细心找一找 2: 如图, 点O为直线AB上一点, ∠AOB=Rt ∠, OD是∠BOC内的一条射线。图中有哪角是互补?有哪角是互余?说明你的理由。互补:小结:互余:∠AOD与 ∠BOD∠COD与 ∠BOD∠AOC与 ∠BOC 强调互余、互补定义题组一.强化概念教学过程3.我来试一试: 没有 85°85°175°58° 148°45° 135° 103°13°从上面这张表格中,你能得到什么信息? 90°-x ( 0°<x< 90°)题组一.强化概念教学过程(2) 图中∠α的余角∠1,∠2的大小有什么关系? 为什么?(3) 这一结论用文字怎么叙述?同角的余角相等(1) 动手画一画: 已知∠α(如图),请利用三角板画的∠α的余角解: ∵∠1=90°-∠α,
∠2=90°-∠ α∴∠1=∠2.余角(补角)性质教学过程图2中∠α与∠1互余,∠β与∠2互余,且∠α = ∠β,∠1与∠2的大小有什么关系?为什么?同角 的余角相等等( )∵∠α与∠1互余∴∠α+∠1=90°,
即∠1=90°-∠α∵∠β与∠2互余∴∠β+∠2=90°,
即∠2=90°-∠β又∵∠α=∠β∴∠1=∠2图2.余角性质教学过程根据上面的讨论,你认为同角或等角的补角
是否也相等?你能结合图形说说你的理由吗?又∵∠α=∠β∴∠1=∠2∵∠1=90°-∠α,
∠2=90°-∠β同 角的补角相等等( ).(类比)补角性质等( )同 角的余角相等教学过程(例1几何说理题简单模仿)例1:如图、已知∠AOC= ∠BOD=Rt ∠。指出图中还有哪些角相等, 并说明理由。理由:解:∠COD +∠BOC=Rt ∠∴ ∠AOB +∠BOC=Rt ∠即∠AOB与 ∠COD都是∠BOC的余角∠AOB=∠COD (同角的余角相等)∠AOB= ∠COD∵ ∠AOC= ∠BOD=Rt ∠余、补角的性质应用例举教学过程试一试:看谁会 如图A、B、O在同一直线上, ∠1= ∠2、找出图中①相等的角②互补的角。∠1与∠BOC互补的角有:解: ∠2与∠AOD∠1与∠AOD∠2与∠ BOC 相等的角有: ∠AOD= ∠BOC补角的性质应用例举1教学过程已知一个的补角是这个角的余角的4倍,求这个角的度数。 (重难点,分析、格式)提问:例2:1:一个角的余角、补角怎样表示?3:能否根据题意列出等量关系。解得: x = 60°解 :180-x = 4(90-x)2:若设这个角为x度,则其余角是_________度,补角是__________度。(90 – x)(180 – x)答:这个角的度数是60°
余、补角的性质应用例举2教学过程做一做(配合例2、学生板演)3 :已知一个角的补角是它的2.5倍。求这个角的余角。2 :若∠1的补角是∠1的3倍。求∠1的度数。1:已知∠α的余角是∠α的2倍。求 ∠α的度数。 ( 解得:∠α = 30o )( 解得:这个角的余角60o)( 解得:∠1 = 45o )题组二(应用)教学过程∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等同角或等角的补角相等. 理一理 . 今天学习的知识小结教学过程 如何测出∠α的度数,请问大家有什么简单的方法?小结小结小结∠1+ ∠2 + ∠3 = 90 °则∠1∠2 ∠3互余 ( )
(2) 一个角的余角一定比这个角的补角小。 ( )
(3) 若? AOB与? BOC互补,则A、O、C同在一直线上。 ( )??辩一辩:拓展提高?教学过程方向角.见教材游戏:折一折 算一算拓展提高教学过程1. 讲练结合,重视题组训练并适时落实。2. 重视学生主体性,从学生实际出发,充分运用教学直观,呈现知识,并提供学生动手活动机会3.恰当处理教材,合理要求(例1,例2处理).4.创设、提供的情景:典型性、开放性教学设计特点
《图形的初步知识》这一章节是学生平面几何的基础的入门课.作为实验几何向论证几何过渡的重要过程,为以后论证角的相等也打下了良好的基础,也为培养和发展学生的逻辑思维能力、观察分析能力、演绎归纳能力打下了结实的基础。教材分析知识目标 理解余角和补角的概念,掌握余角和补角的概念及性质,并能运用它们解决一些实际问题。能力目标情感目标 经历观察、操作、推理、交流等活动,发展学生的几何概念,初步培养学生的几何推理与表达的能力。能运用方程思想解决几何问题 体验数学知识的发生、发展过程,敢于面对数学活动中的困难,建立学好数学的自信心。教学目标教材分析教学重点:余角和补角的性质应用常常需要 几何说理,或综合运用代数知识,特别是用代数的方法来计算角的度数要求较高.教学难点:余角和补角的概念和性质。教材分析 知识基础上说小学里已经初步接触,本节课是在认识直角、平角的基础上,比较角的大小后,通过数量关系和图形关系学习两角互余、互补的概念和性质。学情分析 本课许多知识的构成与现实生活紧密相连,如方位角等能够吸引学生的注意力,利于培养学生学习数学的兴趣。初一学生逻辑思维能力,抽象能力,几何表达能力都还较弱。必须借助于形象思维。采用多媒体辅助教学,增强图形的动感效应,生动形象的表达图形的变化过程,提高教学效果。教法与学法加强直观教学,感性教学把教学过程转化为观察、发现、动手模仿的过程,提高学生学习的兴趣,增强信心。教法: 学法: 通过模仿、操作学会观察、分析,从具体实例中抽象出数学知识以及一般性的结论的思想方法,运用类比思想和方程思想理解与解决问题。
情景引入(图片)直角纸片的剪与拼得出概念(类比)巩固概念题组训练1(图形语言描述)余、补角的性质(类比总结)例1. 说理(模仿)例2.综合运用(方程思想)题组2小节拓展提高教学流程设计教学过程(方位角)海塘大坝要修复加固,施工前要求先测出大坝的倾斜角(即图中的∠1),坝底是石块堆积而成,量角器无法伸入大坝底部测量,聪明的你有什么简单的方法?想一想教学过程情景引入1. 如图,在你手边直角内任画一条射线把直角分成两部分两部分∠1 和∠2。2. 量出∠1 和∠2的度数并标在角内部.把它们剪开.
动一动,拼一拼教学过程3. 把你所剪的角与旁边的同学所剪的拼一拼能拼出直角吗? 4. 想一想如果两个角要拼成直角,它们的度数有什么要求?教学过程如果两个角的和是直角,就说这两个角 互为余角 (complementary angle) 简称“互余”图形上认识若∠1与∠2能拼成直角,则 ∠1与∠2互余。数量上认识若∠1+∠2 =90°,则 ∠1与∠2互余。
余角的概念ABCO教学过程 如果两个角的和等于180° (平角),就说这两个角 互为补角 (supplementary angle) 简称“互补”。运用类比思想图形上认识若∠1与∠2能拼成平角,则 ∠1与∠2互补。数量上认识若∠1+∠2 =180°,则 ∠1与∠2互补。
补角的概念1.读一读.理一理
如果 的和是一个 ,那么这两个角叫做 余角,其中一个角是 的余角。
如果 的和是一个 ,那么这两个角叫做 补角,其中一个角是 的补角。
两个角直角互为另一个角两个角互为 另一个角平角教学过程题组一.强化概念2.找朋友:图中给出的各角中,哪些互为余角?哪些互为补角?(注意解题方法指导)°°°°°°°°题组一.强化概念教学过程3.仔细观察,细心找一找 2: 如图, 点O为直线AB上一点, ∠AOB=Rt ∠, OD是∠BOC内的一条射线。图中有哪角是互补?有哪角是互余?说明你的理由。互补:小结:互余:∠AOD与 ∠BOD∠COD与 ∠BOD∠AOC与 ∠BOC 强调互余、互补定义题组一.强化概念教学过程3.我来试一试: 没有 85°85°175°58° 148°45° 135° 103°13°从上面这张表格中,你能得到什么信息? 90°-x ( 0°<x< 90°)题组一.强化概念教学过程(2) 图中∠α的余角∠1,∠2的大小有什么关系? 为什么?(3) 这一结论用文字怎么叙述?同角的余角相等(1) 动手画一画: 已知∠α(如图),请利用三角板画的∠α的余角解: ∵∠1=90°-∠α,
∠2=90°-∠ α∴∠1=∠2.余角(补角)性质教学过程图2中∠α与∠1互余,∠β与∠2互余,且∠α = ∠β,∠1与∠2的大小有什么关系?为什么?同角 的余角相等等( )∵∠α与∠1互余∴∠α+∠1=90°,
即∠1=90°-∠α∵∠β与∠2互余∴∠β+∠2=90°,
即∠2=90°-∠β又∵∠α=∠β∴∠1=∠2图2.余角性质教学过程根据上面的讨论,你认为同角或等角的补角
是否也相等?你能结合图形说说你的理由吗?又∵∠α=∠β∴∠1=∠2∵∠1=90°-∠α,
∠2=90°-∠β同 角的补角相等等( ).(类比)补角性质等( )同 角的余角相等教学过程(例1几何说理题简单模仿)例1:如图、已知∠AOC= ∠BOD=Rt ∠。指出图中还有哪些角相等, 并说明理由。理由:解:∠COD +∠BOC=Rt ∠∴ ∠AOB +∠BOC=Rt ∠即∠AOB与 ∠COD都是∠BOC的余角∠AOB=∠COD (同角的余角相等)∠AOB= ∠COD∵ ∠AOC= ∠BOD=Rt ∠余、补角的性质应用例举教学过程试一试:看谁会 如图A、B、O在同一直线上, ∠1= ∠2、找出图中①相等的角②互补的角。∠1与∠BOC互补的角有:解: ∠2与∠AOD∠1与∠AOD∠2与∠ BOC 相等的角有: ∠AOD= ∠BOC补角的性质应用例举1教学过程已知一个的补角是这个角的余角的4倍,求这个角的度数。 (重难点,分析、格式)提问:例2:1:一个角的余角、补角怎样表示?3:能否根据题意列出等量关系。解得: x = 60°解 :180-x = 4(90-x)2:若设这个角为x度,则其余角是_________度,补角是__________度。(90 – x)(180 – x)答:这个角的度数是60°
余、补角的性质应用例举2教学过程做一做(配合例2、学生板演)3 :已知一个角的补角是它的2.5倍。求这个角的余角。2 :若∠1的补角是∠1的3倍。求∠1的度数。1:已知∠α的余角是∠α的2倍。求 ∠α的度数。 ( 解得:∠α = 30o )( 解得:这个角的余角60o)( 解得:∠1 = 45o )题组二(应用)教学过程∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等同角或等角的补角相等. 理一理 . 今天学习的知识小结教学过程 如何测出∠α的度数,请问大家有什么简单的方法?小结小结小结∠1+ ∠2 + ∠3 = 90 °则∠1∠2 ∠3互余 ( )
(2) 一个角的余角一定比这个角的补角小。 ( )
(3) 若? AOB与? BOC互补,则A、O、C同在一直线上。 ( )??辩一辩:拓展提高?教学过程方向角.见教材游戏:折一折 算一算拓展提高教学过程1. 讲练结合,重视题组训练并适时落实。2. 重视学生主体性,从学生实际出发,充分运用教学直观,呈现知识,并提供学生动手活动机会3.恰当处理教材,合理要求(例1,例2处理).4.创设、提供的情景:典型性、开放性教学设计特点
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
