3.3 立方根
图片预览




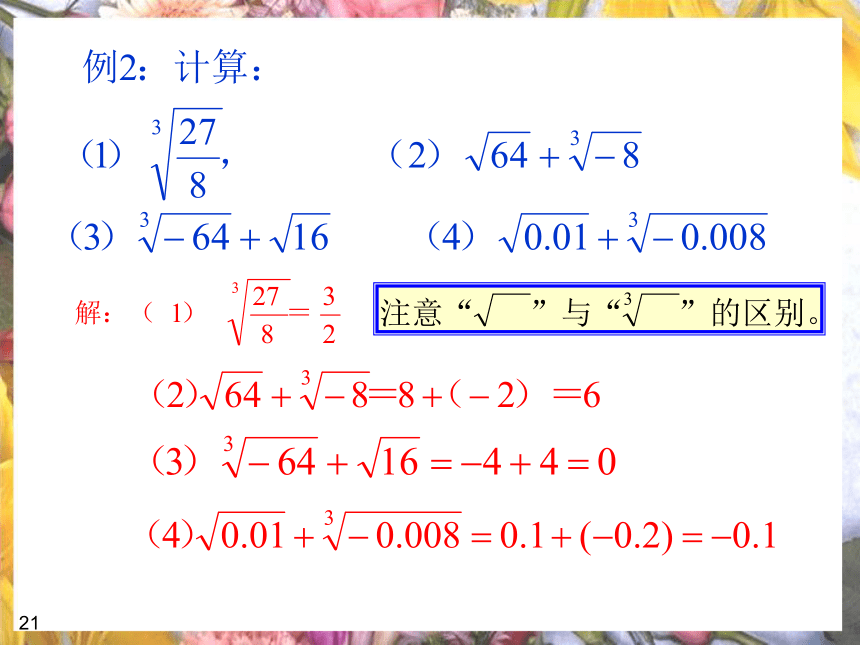

文档简介
课件15张PPT。渎浦校区厄尔诺·鲁比克 三阶魔方三阶魔方第一层有多少个立方体?
它一共由多少个小立方体组成的?由8个小立方体组成的是几阶魔方你知道吗?二阶魔方64个呢?四阶魔方5立方根定义: 一般地,一个数的立方等于a,
这个数就叫做a的立方根,也叫做a的三次方根,
记作 ,其中a 是被开方数,3是根指数,
符号“ ”读做“三次根号”。关于a的问题:(1)有几个数的立方等于8?
(2)有没有一个数的立方等于-8?
(3)有没有一个数的立方等于0?平方根定义:一般地,一个数的平方等于a,
这个数就叫做a的平方根,也叫做a的二次方根。类比
思想10关于3的问题:(1)这个3能不能省略?例1:求下列各数的立方根:(1)125 (2) (3)-0.064 (4)0 (5)-27 ∵ ,
∴ ,观察并思考:一个数的立方根的个数有几个?
一个数的立方根的符号与这个数的符号存在什么关系? 一个正数有一个正的立方根,
一个负数有一个负的立方根,
零的立方根是零。求一个数的立方根的运算,叫做开立方。 分类讨论
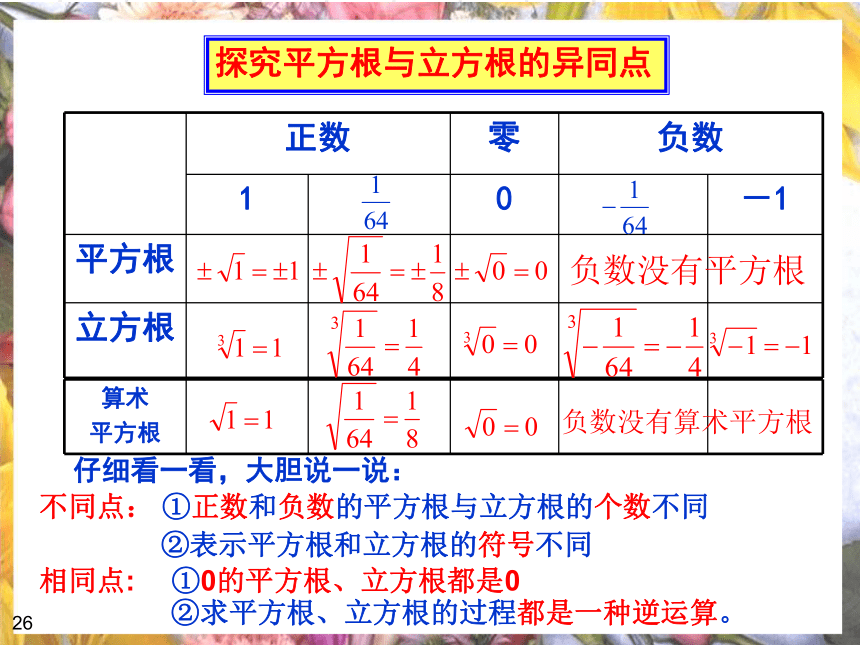
思想1621探究平方根与立方根的异同点仔细看一看,大胆说一说:不同点: ①正数和负数的平方根与立方根的个数不同
相同点: ①0的平方根、立方根都是0
②表示平方根和立方根的符号不同②求平方根、立方根的过程都是一种逆运算。261.判断下列说法是否正确,并说明理由:
(1) 的立方根是
(2)算术平方根和立方根都等于本身的数只有0
(3)-8的立方根是-2,但-8没有平方根
(4) 4的平方根是±2,但4没有立方根
(5)互为相反数的两个数的立方根也互为相反数明辨是非×√×√举例时要注意特殊数:1,0,-1举例的数
要有代表性31×帮忙纠错433?下一页学以致用(1)如图,是由若干个棱长为1的小立方体摆成的一
个长方体,你能否利用这些小立方体摆成一个
立方体呢(全部用完)?37(2)把一个长、宽、高分别为50cm,8cm,20cm的长方体铁块溶化后锻造成一个立方体铁块,问造成的立方体的棱长是多少cm?(损耗忽略不计)下一页课堂缩影我们可以提出哪些问题?(1)它表示什么意思?(2)计算的结果是多少?(6)生活当中 表示的实际意义可以是什么?… …(4)如果把64改为-64后计算的结果又是多少?(5)如果把64改为46后计算的结果你知道吗?提出一个问题比解决一个问题更重要
----------------------爱因斯坦45家庭作业(1)课堂作业本3.3(2)课本剩余作业题(3)提高题 合作探究(3)方案设计:有个魔方加工车间在加工魔方,
最后还剩下155个棱长为1的小立方体未加工成
魔方(二阶魔方、三阶魔方或四阶魔方),
如果你是该车间的主管,你能设计一种生产
方案,把这155个小立方体全部加工成魔方吗?
请计算出你的方案共加工成几个魔方。方案一方案二方案三下一页48方案一:返回方案二方案三方案二:返回方案一方案三方案三:返回方案一方案二
它一共由多少个小立方体组成的?由8个小立方体组成的是几阶魔方你知道吗?二阶魔方64个呢?四阶魔方5立方根定义: 一般地,一个数的立方等于a,
这个数就叫做a的立方根,也叫做a的三次方根,
记作 ,其中a 是被开方数,3是根指数,
符号“ ”读做“三次根号”。关于a的问题:(1)有几个数的立方等于8?
(2)有没有一个数的立方等于-8?
(3)有没有一个数的立方等于0?平方根定义:一般地,一个数的平方等于a,
这个数就叫做a的平方根,也叫做a的二次方根。类比
思想10关于3的问题:(1)这个3能不能省略?例1:求下列各数的立方根:(1)125 (2) (3)-0.064 (4)0 (5)-27 ∵ ,
∴ ,观察并思考:一个数的立方根的个数有几个?
一个数的立方根的符号与这个数的符号存在什么关系? 一个正数有一个正的立方根,
一个负数有一个负的立方根,
零的立方根是零。求一个数的立方根的运算,叫做开立方。 分类讨论
思想1621探究平方根与立方根的异同点仔细看一看,大胆说一说:不同点: ①正数和负数的平方根与立方根的个数不同
相同点: ①0的平方根、立方根都是0
②表示平方根和立方根的符号不同②求平方根、立方根的过程都是一种逆运算。261.判断下列说法是否正确,并说明理由:
(1) 的立方根是
(2)算术平方根和立方根都等于本身的数只有0
(3)-8的立方根是-2,但-8没有平方根
(4) 4的平方根是±2,但4没有立方根
(5)互为相反数的两个数的立方根也互为相反数明辨是非×√×√举例时要注意特殊数:1,0,-1举例的数
要有代表性31×帮忙纠错433?下一页学以致用(1)如图,是由若干个棱长为1的小立方体摆成的一
个长方体,你能否利用这些小立方体摆成一个
立方体呢(全部用完)?37(2)把一个长、宽、高分别为50cm,8cm,20cm的长方体铁块溶化后锻造成一个立方体铁块,问造成的立方体的棱长是多少cm?(损耗忽略不计)下一页课堂缩影我们可以提出哪些问题?(1)它表示什么意思?(2)计算的结果是多少?(6)生活当中 表示的实际意义可以是什么?… …(4)如果把64改为-64后计算的结果又是多少?(5)如果把64改为46后计算的结果你知道吗?提出一个问题比解决一个问题更重要
----------------------爱因斯坦45家庭作业(1)课堂作业本3.3(2)课本剩余作业题(3)提高题 合作探究(3)方案设计:有个魔方加工车间在加工魔方,
最后还剩下155个棱长为1的小立方体未加工成
魔方(二阶魔方、三阶魔方或四阶魔方),
如果你是该车间的主管,你能设计一种生产
方案,把这155个小立方体全部加工成魔方吗?
请计算出你的方案共加工成几个魔方。方案一方案二方案三下一页48方案一:返回方案二方案三方案二:返回方案一方案三方案三:返回方案一方案二
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
