4.2.1平面直角坐标系 课件 (共14张PPT) 浙教版数学八年级上册
文档属性
| 名称 | 4.2.1平面直角坐标系 课件 (共14张PPT) 浙教版数学八年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 17:52:30 | ||
图片预览

文档简介
(共14张PPT)
浙教版数学八年级上册第四单元第二节第一课时
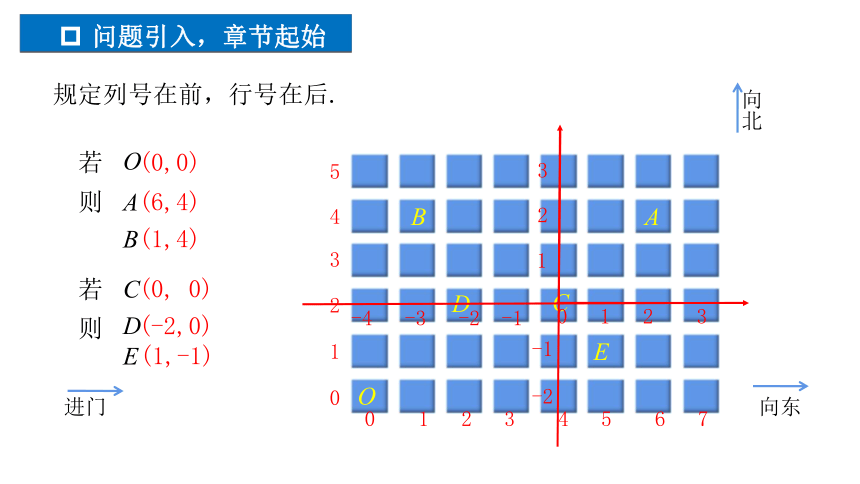
问题引入,章节起始
O
0 1 2 3 4 5 6 7
0
2
3
4
5
1
进门
A
向东
规定列号在前,行号在后.
向北
B
D
C
E
-4 -3 -2 -1
O
(0,0)
若
则
A
(6,4)
B
(1,4)
C
(0, 0)
若
则
D
(-2,0)
E
(1,-1)
0 1 2 3
3
2
1
-1
-2
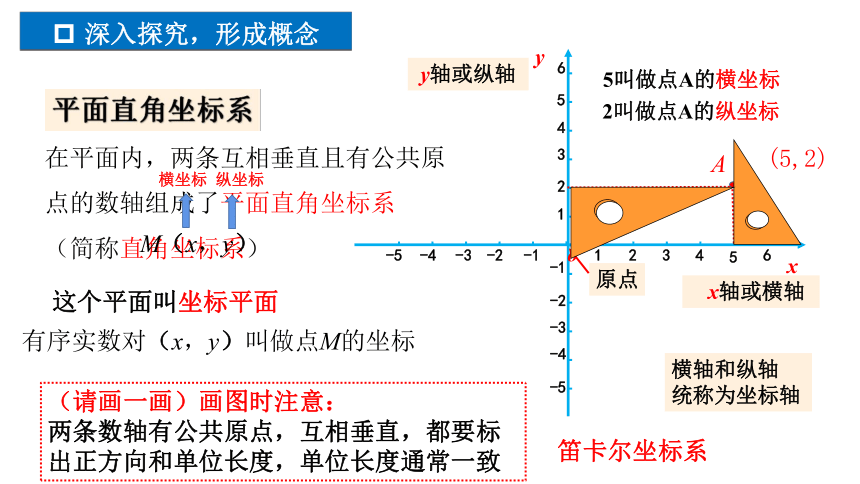
在平面内,两条互相垂直且有公共原 点的数轴组成了平面直角坐标系 (简称直角坐标系)
1
2
3
4
5
6
-1
-2
-3
-4
-5
y
x
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
这个平面叫坐标平面
原点
x轴或横轴
横轴和纵轴
统称为坐标轴
y轴或纵轴
(请画一画)画图时注意:
两条数轴有公共原点,互相垂直,都要标出正方向和单位长度,单位长度通常一致
深入探究,形成概念
A
(5,2)
M(x,y)
横坐标
纵坐标
有序实数对(x,y)叫做点M的坐标
5叫做点A的横坐标
2叫做点A的纵坐标
笛卡尔坐标系
1
2
3
4
5
6
-1
-2
-3
-4
-5
y
x
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
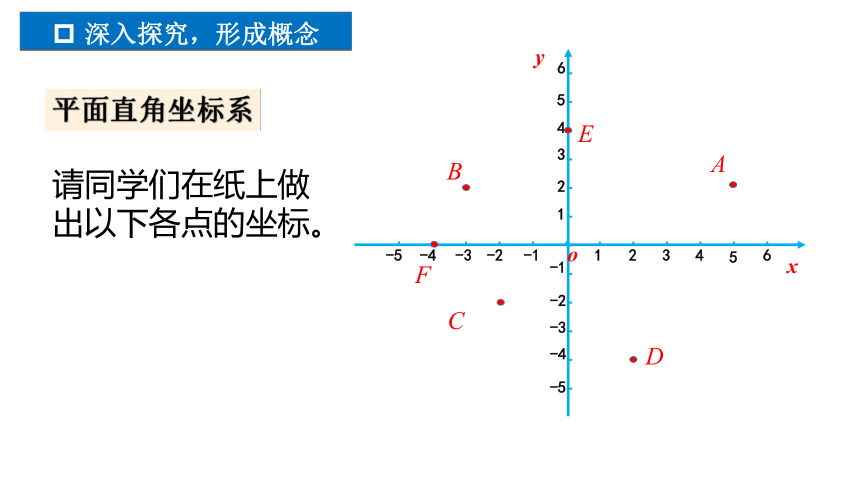
深入探究,形成概念
A
B
C
D
F
E
请同学们在纸上做出以下各点的坐标。
第四象限
第一象限
第二象限
第三象限
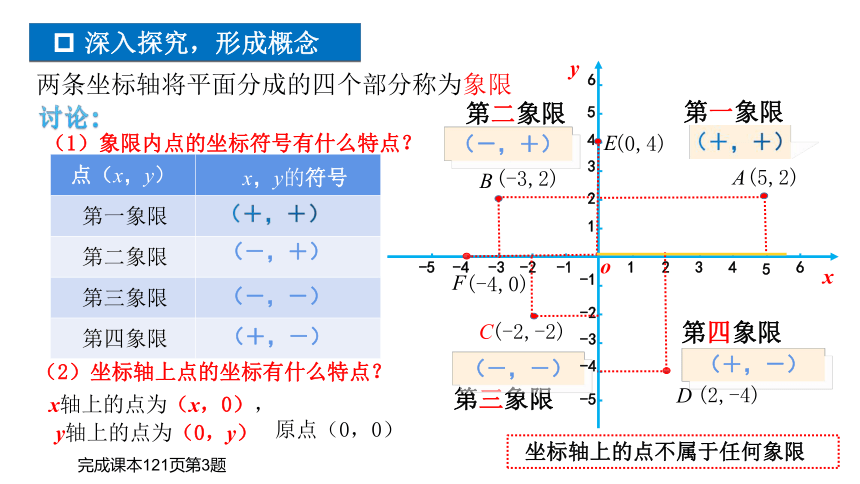
两条坐标轴将平面分成的四个部分称为象限
(1)象限内点的坐标符号有什么特点?
(2)坐标轴上点的坐标有什么特点?
(-,+)
(-,-)
(+,-)
深入探究,形成概念
坐标轴上的点不属于任何象限
深入探究,形成概念
1
2
3
4
5
6
-1
-2
-3
-4
-5
y
x
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
点(x,y)
x,y的符号
第一象限
第二象限
第三象限
第四象限
A
B
C
D
(5,2)
(-3,2)
(-2,-2)
(2,-4)
F
E
(0,4)
(-4,0)
(-,+)
(-,-)
(+,-)
x轴上的点为(x,0),
y轴上的点为(0,y)
原点(0,0)
完成课本121页第3题
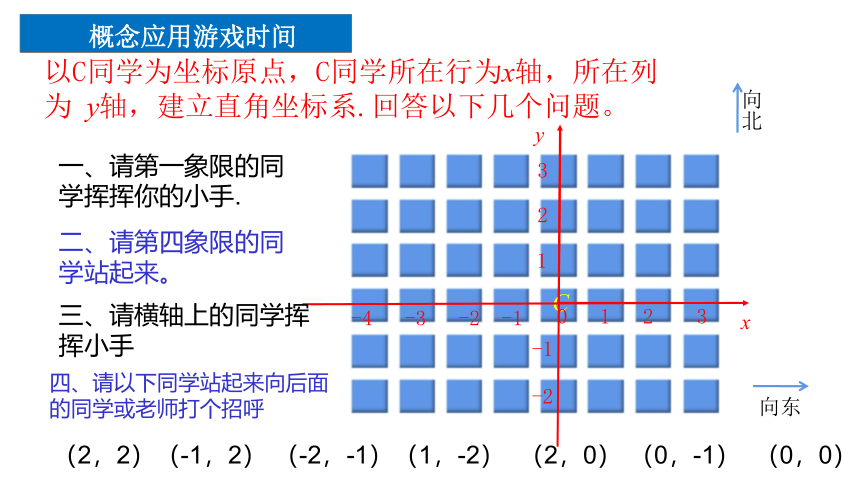
概念应用游戏时间
向东
向北
C
-4 -3 -2 -1
0 1 2 3
3
2
1
-1
-2
以C同学为坐标原点,C同学所在行为x轴,所在列为 y轴,建立直角坐标系. 回答以下几个问题。
y
x
一、请第一象限的同学挥挥你的小手.
二、请第四象限的同学站起来。
三、请横轴上的同学挥挥小手
四、请以下同学站起来向后面的同学或老师打个招呼
(2,2)(-1,2) (-2,-1)(1,-2) (2,0) (0,-1) (0,0)
-1
x
N
P
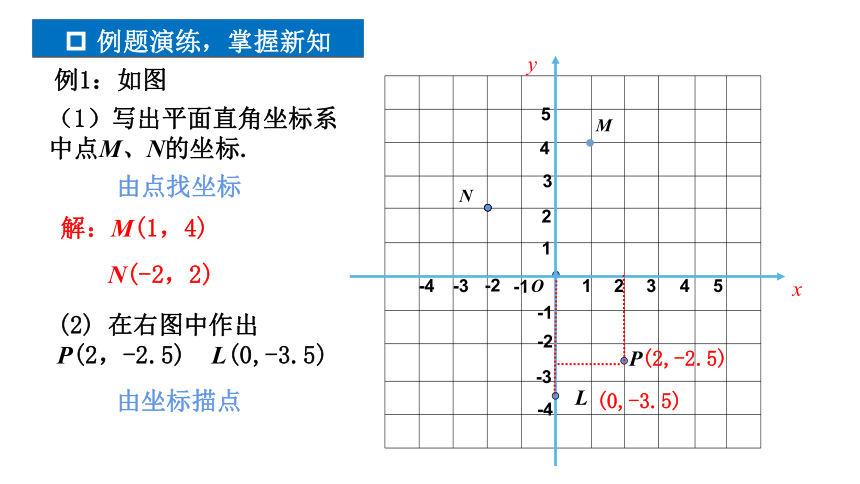
例1:如图
2
1
5
4
3
-4
-2
-1
-3
y
4
3
2
1
5
-2
-3
-4
O
L
解:M(1,4)
N(-2,2)
(2) 在右图中作出 P(2,-2.5) L(0,-3.5)
由点找坐标
例题演练,掌握新知
例题演练,掌握新知
(1)写出平面直角坐标系中点M、N的坐标.
(2,-2.5)
(0,-3.5)
由坐标描点
M
-1
x
N
P
例1:如图
2
1
5
4
3
-4
-2
-1
-3
y
4
3
2
1
5
-2
-3
-4
O
L
例题演练,掌握新知
例题演练,掌握新知
(2,-2.5)
(0,-3.5)
M
结论:
建立了平面直角坐标系后,
对于平面内任意一点
我们都可以确定它的坐标,
反之,对于任何一个坐标,
我们都可以在坐标平面内找到这个点.
即坐标平面内点与坐标之间
是一一对应关系
-1
x
N
P
例1:如图
2
1
5
4
3
-4
-2
-1
-3
y
4
3
2
1
5
-2
-3
-4
O
L
例题演练,掌握新知
例题演练,掌握新知
(2,-2.5)
(0,-3.5)
M
(3)点M到x轴的距离是 .
点M到y轴的距离是 .
点M到原点的距离是 .
结论:
对于任意点A(x,y)
到x轴的距离是 .
到y轴的距离是 .
E
F
(1,4)
4
1
深化拓展,体悟新知
1.在点A(-2,-4),B(-2,4),C(3,-4),D(3,4), E(-1,0), F(0,8),G(2,-4),H (0,-5)中
属于第三象限的点是 ,属于第四象限的点是 .
在x轴上的点是 , 在y轴上的点是 .
A
G
E
C ,
H
F ,
深化拓展,体悟新知
1.已知点M(2-m,m-1),
(1)当点M在x轴上时,求m的值.
解:依题意得, m-1=0, 即m=1.
(2)当点M在第二象限时,
求m的取值范围.
解:依题意得,
∴m>2.
(3)当点M到y轴的距离是2时,求m的值.
y
x
A(x ,y)
x
y
o
点A到x轴的距离是
点A到y轴的距离是
|y|
|x|
解:依题意得,|2-m|=2,
∴2-m=2 或2-m=-2
∴m=0或4
2-m<0
m-1>0
深化拓展,体悟新知
1.已知点M(2-m,m-1),
(4)当点M到 x轴和y轴的距离相等,求m的值.
2.变式:已知点A到 x轴和y轴的距离为3,求点A的坐标。
综合应用,内化新知
3.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,求点P的坐标.
x
y
-4
o
1
2
3
4
-3
-2
3
1
4
2
-2
-4
-1
-3
-4 -3 -2 -1 1 2 3 4
4
3
2
1
-1
-2
-3
-4
A
小结新课,梳理新知
平面直角坐标系
象限内点的坐标特点
坐标轴上点的坐标特点
x轴上的点纵坐标为0,
记为(x,0)
y轴上的点横坐标为0,
记为(0,y)
对于任意点A(x,y)
到x轴的距离是 .
到y轴的距离是 .
数形结合思想
分类讨论思想
求点的坐标
浙教版数学八年级上册第四单元第二节第一课时
问题引入,章节起始
O
0 1 2 3 4 5 6 7
0
2
3
4
5
1
进门
A
向东
规定列号在前,行号在后.
向北
B
D
C
E
-4 -3 -2 -1
O
(0,0)
若
则
A
(6,4)
B
(1,4)
C
(0, 0)
若
则
D
(-2,0)
E
(1,-1)
0 1 2 3
3
2
1
-1
-2
在平面内,两条互相垂直且有公共原 点的数轴组成了平面直角坐标系 (简称直角坐标系)
1
2
3
4
5
6
-1
-2
-3
-4
-5
y
x
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
这个平面叫坐标平面
原点
x轴或横轴
横轴和纵轴
统称为坐标轴
y轴或纵轴
(请画一画)画图时注意:
两条数轴有公共原点,互相垂直,都要标出正方向和单位长度,单位长度通常一致
深入探究,形成概念
A
(5,2)
M(x,y)
横坐标
纵坐标
有序实数对(x,y)叫做点M的坐标
5叫做点A的横坐标
2叫做点A的纵坐标
笛卡尔坐标系
1
2
3
4
5
6
-1
-2
-3
-4
-5
y
x
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
深入探究,形成概念
A
B
C
D
F
E
请同学们在纸上做出以下各点的坐标。
第四象限
第一象限
第二象限
第三象限
两条坐标轴将平面分成的四个部分称为象限
(1)象限内点的坐标符号有什么特点?
(2)坐标轴上点的坐标有什么特点?
(-,+)
(-,-)
(+,-)
深入探究,形成概念
坐标轴上的点不属于任何象限
深入探究,形成概念
1
2
3
4
5
6
-1
-2
-3
-4
-5
y
x
1
2
3
4
5
6
-1
-2
-3
-4
-5
o
点(x,y)
x,y的符号
第一象限
第二象限
第三象限
第四象限
A
B
C
D
(5,2)
(-3,2)
(-2,-2)
(2,-4)
F
E
(0,4)
(-4,0)
(-,+)
(-,-)
(+,-)
x轴上的点为(x,0),
y轴上的点为(0,y)
原点(0,0)
完成课本121页第3题
概念应用游戏时间
向东
向北
C
-4 -3 -2 -1
0 1 2 3
3
2
1
-1
-2
以C同学为坐标原点,C同学所在行为x轴,所在列为 y轴,建立直角坐标系. 回答以下几个问题。
y
x
一、请第一象限的同学挥挥你的小手.
二、请第四象限的同学站起来。
三、请横轴上的同学挥挥小手
四、请以下同学站起来向后面的同学或老师打个招呼
(2,2)(-1,2) (-2,-1)(1,-2) (2,0) (0,-1) (0,0)
-1
x
N
P
例1:如图
2
1
5
4
3
-4
-2
-1
-3
y
4
3
2
1
5
-2
-3
-4
O
L
解:M(1,4)
N(-2,2)
(2) 在右图中作出 P(2,-2.5) L(0,-3.5)
由点找坐标
例题演练,掌握新知
例题演练,掌握新知
(1)写出平面直角坐标系中点M、N的坐标.
(2,-2.5)
(0,-3.5)
由坐标描点
M
-1
x
N
P
例1:如图
2
1
5
4
3
-4
-2
-1
-3
y
4
3
2
1
5
-2
-3
-4
O
L
例题演练,掌握新知
例题演练,掌握新知
(2,-2.5)
(0,-3.5)
M
结论:
建立了平面直角坐标系后,
对于平面内任意一点
我们都可以确定它的坐标,
反之,对于任何一个坐标,
我们都可以在坐标平面内找到这个点.
即坐标平面内点与坐标之间
是一一对应关系
-1
x
N
P
例1:如图
2
1
5
4
3
-4
-2
-1
-3
y
4
3
2
1
5
-2
-3
-4
O
L
例题演练,掌握新知
例题演练,掌握新知
(2,-2.5)
(0,-3.5)
M
(3)点M到x轴的距离是 .
点M到y轴的距离是 .
点M到原点的距离是 .
结论:
对于任意点A(x,y)
到x轴的距离是 .
到y轴的距离是 .
E
F
(1,4)
4
1
深化拓展,体悟新知
1.在点A(-2,-4),B(-2,4),C(3,-4),D(3,4), E(-1,0), F(0,8),G(2,-4),H (0,-5)中
属于第三象限的点是 ,属于第四象限的点是 .
在x轴上的点是 , 在y轴上的点是 .
A
G
E
C ,
H
F ,
深化拓展,体悟新知
1.已知点M(2-m,m-1),
(1)当点M在x轴上时,求m的值.
解:依题意得, m-1=0, 即m=1.
(2)当点M在第二象限时,
求m的取值范围.
解:依题意得,
∴m>2.
(3)当点M到y轴的距离是2时,求m的值.
y
x
A(x ,y)
x
y
o
点A到x轴的距离是
点A到y轴的距离是
|y|
|x|
解:依题意得,|2-m|=2,
∴2-m=2 或2-m=-2
∴m=0或4
2-m<0
m-1>0
深化拓展,体悟新知
1.已知点M(2-m,m-1),
(4)当点M到 x轴和y轴的距离相等,求m的值.
2.变式:已知点A到 x轴和y轴的距离为3,求点A的坐标。
综合应用,内化新知
3.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,求点P的坐标.
x
y
-4
o
1
2
3
4
-3
-2
3
1
4
2
-2
-4
-1
-3
-4 -3 -2 -1 1 2 3 4
4
3
2
1
-1
-2
-3
-4
A
小结新课,梳理新知
平面直角坐标系
象限内点的坐标特点
坐标轴上点的坐标特点
x轴上的点纵坐标为0,
记为(x,0)
y轴上的点横坐标为0,
记为(0,y)
对于任意点A(x,y)
到x轴的距离是 .
到y轴的距离是 .
数形结合思想
分类讨论思想
求点的坐标
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
