2.1 直线与圆的位置关系(1)课件(共29张PPT)浙教版九年级下册
文档属性
| 名称 | 2.1 直线与圆的位置关系(1)课件(共29张PPT)浙教版九年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 11:20:15 | ||
图片预览








文档简介
(共29张PPT)
1、点与圆有几种位置关系?
复习提问:
2、怎样判定点和圆的位置关系?
.A
.A
.A
.A
.A
. B
.A
.A
.C
.A
.A
(1)点到圆心的距离____半径时,点在圆外。
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。
大于
等于
小于
单车欲问边,属国过居延。 征蓬出汉塞,归雁入胡天。 大漠孤烟直,长河落日圆。 萧关逢候骑,都护在燕然。
使至塞上
王 维
大漠孤烟直,长河落日圆。
一、新课引入
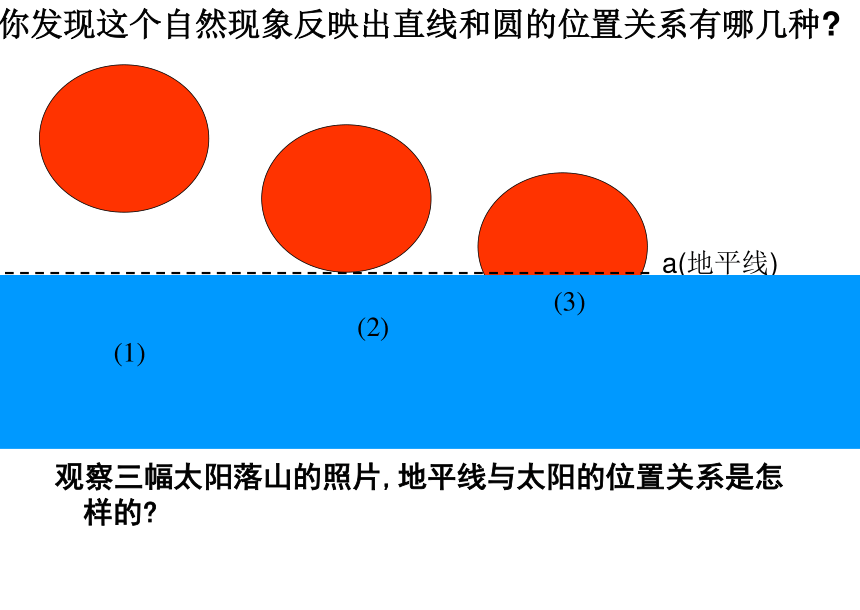
1、“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线与圆的公共点的个数想象一下,直线和圆的位置关系有几种?
观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的
a(地平线)
你发现这个自然现象反映出直线和圆的位置关系有哪几种
(1)
(3)
(2)
(1)直线和圆有两个公共点时,叫做直线和圆相交; 这时直线叫做圆的割线.
(2)直线和圆有唯一公共点时,叫做直线和圆相切;这时直线叫做圆的切线. 唯一的公共点叫做切点.
(3)直线和圆没有公共点时,叫做直线和圆相离.
(3)
(2)
.O
.O
l
l
(1)
.O
切点
切线
交点
快速判断下列各图中直线与圆的位置关系
.O
l
.O1
.O
l
.O2
l
.
l
o
.O
是是非非
1、直线与圆最多有两个公共
点 。…………………( )
√
.O
是是非非
×
.C
2、若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )
是是非非
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
×
.A1
.B1
.O
.A
.B
.B2
.A2
是是非非
√
.
C
4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )
.
O
l
T
.O
d
思考:①所画的圆与直线 l 有什么位置关系
②你能从d与r的大小关系来判断直线 l 与圆的位置关系吗
l
T
.O
d
l
T
.O
d
直线与圆的位置关系
当d>r 那么直线l与⊙O相离
当d=r 那么直线l与⊙O相切
当dd表示圆心O到直线l的距离,r表示⊙O的半径
r
r
r
小结:
判定直线与圆的位置关系的方法有____种:
(1)由________________ 的个数来判断;
(2)由___________________________ 的
数量大小关系来判断.
注意:在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
O
l
O
l
O
l
r
d
┐
┐
d
┐
d
直线与圆的位置关系判定方法:
无
切线
割线
直线名称
无
切点
交点
公共点名称
d > r
d = r
d < r
圆心到直线距离
d 与半径 r 关系
0
1
2
公共点个数
相离
相切
相交
直线和圆的位置关系
1 、 设⊙O的半径为r,圆心O到直线l的距离为d。根据下列条件判断直线l与⊙O的位置关系。
(2)d= ,r= ;
(3)d=2,r=2;
(1)d=4,r=3;
相离
相交
相切
2、已知⊙O的半径为4, 点A在直线l上, 且OA=4,则l一定和圆O相切吗?为什么?请画图说明。
4
O.
A
l
l
A
.O
4
练习:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,
以C为圆心,r为半径的圆与直线AB有怎样的位置
关系 为什么
D
AB= = =5
即圆心C到AB的距离 d=2.4cm
CD = = =2.4(cm)
解:过C作CD⊥AB,垂足为D,则在Rt△ABC中,
在△ABC中,∠ACB=90°,AC=3cm , BC=4cm
(1)r=2cm; (2) r=2.4cm; (3) r=3 cm.
根据三角形的面积公式有
D
(1)r=2cm; (2)r=2.4cm; (3)r=3cm.
当r =2.4cm时,
d = r,
∴☉C 与直线AB相切.
当r =3cm时,
d < r,
∴☉C 与直线AB相交.
A
当r =2cm时,
d > r,
∴☉C 与直线AB相离.
2.4cm
B
C
D
3cm
4cm
A
B
C
D
3cm
4cm
2.4cm
A
B
C
D
3cm
4cm
2.4cm
A
例1:已知:如图,P是∠ABC的角平分线上一点.
⊙P与BC相切。
求证:⊙P与AB相切.
P
A
C
B
如图,在码头A的北偏东60°方向有一个海岛,离该岛中心P的12海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了10海里到达B,这时岛中心P在北偏东45°方向。若货船不改变航向,问货船会不会进入暗礁区?
A
B
P
H
60°
45°
12
北
10
直线与圆的位置
公共点个数
d与r的关系
公共点名称
2
1
0
dd=r
d>r
切点
无
相交
相切
相离
课堂小结:
1、直线与圆的三种位置关系
2、判定的方法
交点
根据定义
根据 d 与 r 的大小关系(常用)
形
数
1、已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
3)若AB和⊙O相交,则 .
2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
d < 5cm
三、练习
0cm≤
2
1
0
3.直线和圆有2个交点,则直线和圆_________;
直线和圆有1个交点,则直线和圆_________;
直线和圆有没有交点,则直线和圆_________;
相交
相切
相离
B
C
A
D
变式:若要使圆C与AB所在直线只有一个公共点,这时圆C的半径 r 有什么要求?
3
4
当 r = 2.4
或 3 < r ≤ 4时,圆C与线段AB只有一个公共点。
线段AB
布置作业:
1、点与圆有几种位置关系?
复习提问:
2、怎样判定点和圆的位置关系?
.A
.A
.A
.A
.A
. B
.A
.A
.C
.A
.A
(1)点到圆心的距离____半径时,点在圆外。
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。
大于
等于
小于
单车欲问边,属国过居延。 征蓬出汉塞,归雁入胡天。 大漠孤烟直,长河落日圆。 萧关逢候骑,都护在燕然。
使至塞上
王 维
大漠孤烟直,长河落日圆。
一、新课引入
1、“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线与圆的公共点的个数想象一下,直线和圆的位置关系有几种?
观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的
a(地平线)
你发现这个自然现象反映出直线和圆的位置关系有哪几种
(1)
(3)
(2)
(1)直线和圆有两个公共点时,叫做直线和圆相交; 这时直线叫做圆的割线.
(2)直线和圆有唯一公共点时,叫做直线和圆相切;这时直线叫做圆的切线. 唯一的公共点叫做切点.
(3)直线和圆没有公共点时,叫做直线和圆相离.
(3)
(2)
.O
.O
l
l
(1)
.O
切点
切线
交点
快速判断下列各图中直线与圆的位置关系
.O
l
.O1
.O
l
.O2
l
.
l
o
.O
是是非非
1、直线与圆最多有两个公共
点 。…………………( )
√
.O
是是非非
×
.C
2、若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )
是是非非
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
×
.A1
.B1
.O
.A
.B
.B2
.A2
是是非非
√
.
C
4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )
.
O
l
T
.O
d
思考:①所画的圆与直线 l 有什么位置关系
②你能从d与r的大小关系来判断直线 l 与圆的位置关系吗
l
T
.O
d
l
T
.O
d
直线与圆的位置关系
当d>r 那么直线l与⊙O相离
当d=r 那么直线l与⊙O相切
当d
r
r
r
小结:
判定直线与圆的位置关系的方法有____种:
(1)由________________ 的个数来判断;
(2)由___________________________ 的
数量大小关系来判断.
注意:在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
O
l
O
l
O
l
r
d
┐
┐
d
┐
d
直线与圆的位置关系判定方法:
无
切线
割线
直线名称
无
切点
交点
公共点名称
d > r
d = r
d < r
圆心到直线距离
d 与半径 r 关系
0
1
2
公共点个数
相离
相切
相交
直线和圆的位置关系
1 、 设⊙O的半径为r,圆心O到直线l的距离为d。根据下列条件判断直线l与⊙O的位置关系。
(2)d= ,r= ;
(3)d=2,r=2;
(1)d=4,r=3;
相离
相交
相切
2、已知⊙O的半径为4, 点A在直线l上, 且OA=4,则l一定和圆O相切吗?为什么?请画图说明。
4
O.
A
l
l
A
.O
4
练习:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,
以C为圆心,r为半径的圆与直线AB有怎样的位置
关系 为什么
D
AB= = =5
即圆心C到AB的距离 d=2.4cm
CD = = =2.4(cm)
解:过C作CD⊥AB,垂足为D,则在Rt△ABC中,
在△ABC中,∠ACB=90°,AC=3cm , BC=4cm
(1)r=2cm; (2) r=2.4cm; (3) r=3 cm.
根据三角形的面积公式有
D
(1)r=2cm; (2)r=2.4cm; (3)r=3cm.
当r =2.4cm时,
d = r,
∴☉C 与直线AB相切.
当r =3cm时,
d < r,
∴☉C 与直线AB相交.
A
当r =2cm时,
d > r,
∴☉C 与直线AB相离.
2.4cm
B
C
D
3cm
4cm
A
B
C
D
3cm
4cm
2.4cm
A
B
C
D
3cm
4cm
2.4cm
A
例1:已知:如图,P是∠ABC的角平分线上一点.
⊙P与BC相切。
求证:⊙P与AB相切.
P
A
C
B
如图,在码头A的北偏东60°方向有一个海岛,离该岛中心P的12海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了10海里到达B,这时岛中心P在北偏东45°方向。若货船不改变航向,问货船会不会进入暗礁区?
A
B
P
H
60°
45°
12
北
10
直线与圆的位置
公共点个数
d与r的关系
公共点名称
2
1
0
d
d>r
切点
无
相交
相切
相离
课堂小结:
1、直线与圆的三种位置关系
2、判定的方法
交点
根据定义
根据 d 与 r 的大小关系(常用)
形
数
1、已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
3)若AB和⊙O相交,则 .
2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
d < 5cm
三、练习
0cm≤
2
1
0
3.直线和圆有2个交点,则直线和圆_________;
直线和圆有1个交点,则直线和圆_________;
直线和圆有没有交点,则直线和圆_________;
相交
相切
相离
B
C
A
D
变式:若要使圆C与AB所在直线只有一个公共点,这时圆C的半径 r 有什么要求?
3
4
当 r = 2.4
或 3 < r ≤ 4时,圆C与线段AB只有一个公共点。
线段AB
布置作业:
