第1章 解直角三角形(单元小结)-2023-2024学年九年级数学下册同步精品课堂(浙教版)
文档属性
| 名称 | 第1章 解直角三角形(单元小结)-2023-2024学年九年级数学下册同步精品课堂(浙教版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-25 00:00:00 | ||
图片预览











文档简介
单元小结
数学(浙教版)
九年级 下册
第1章 解直角三角形
单元小结
知识点一 锐角三角函数
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
如图所示,在Rt△ABC中,∠C=90°,
a,b,c分别是∠A,∠B,∠C的对边.
(1) ∠A的正弦:
∠A的对边
斜边
sin A =
∠A的邻边
斜边
∠A的邻边
∠A的对边
单元小结
知识点二 特殊角的三角函数值
sin30°= ,sin45°= ,sin60°= ;
cos30°= ,cos45°= ,cos60°= ;
tan30°= ,tan45°= ,tan60°= .
1
单元小结
知识点三 解直角三角形
(1) 在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
三边关系: ;
三角关系: ;
边角关系:sinA=cosB= ,cosA=sinB = ,
tanA= ,tanB= .
a2+b2=c2
∠A=90°-∠B
单元小结
(2) 直角三角形可解的条件和解法
?条件:解直角三角形时知道其中的2个元素(至少有一个是边),就可以求出其余的3个未知元素.
?解法:①一边一锐角,先由两锐角互余关系求出另一锐角;知斜边,再用正弦(或余弦)求另两边;知直角边用正切求另一直角边,再用正弦或勾股定理求斜边;②知两边:先用勾股定理求另一边,再用边角关系求锐角;③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.
单元小结
(3) 互余两角的三角函数间的关系
sinα = ,
cosα = ,
sin2α + cos2α = .
tanα · tan(90°-α) = .
cos(90°-α)
sin(90°-α)
1
1
对于sinα与tanα,角度越大,函数值越 ;
对于cosα,角度越大,函数值越 .
大
小
(4) 锐角三角函数的增减性
单元小结
知识点四 借助计算器求锐角三角函数值及锐角
(1) 利用计算器求三角函数值
第二步:输入角度值,
屏幕显示结果.
(也有的计算器是先输入角度再按函数名称键)
第一步:按计算器 键,
sin
tan
cos
单元小结
(2) 利用计算器求锐角的度数
还可以利用 键,进一步得到角的度数.
第二步:输入函数值
屏幕显示答案 (按实际需要进行精确)
方法①:
°'″
2nd F
第一步:按计算器 键,
2nd F
sin
cos
tan
方法②:
第二步:输入锐角函数值
屏幕显示答案 (按实际需要选取精确值).
第一步:按计算器 键,
°'″
2nd F
单元小结
知识点五 三角函数的应用
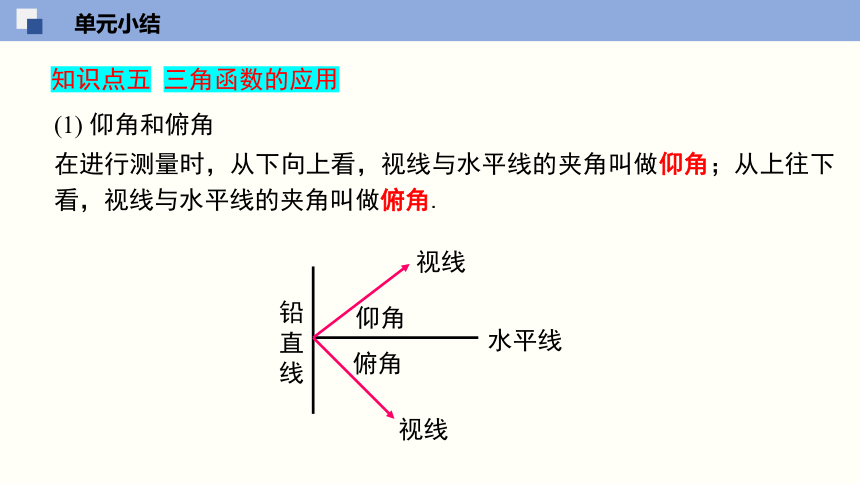
(1) 仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
单元小结
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角. 如图所示:
30°
45°
B
O
A
东
西
北
南
(2) 方位角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
单元小结
坡面与水平面的夹角叫做坡角,记作α,有 i = tan α.
坡度通常写成1∶m的形式,如i=1∶6.
显然,坡度越大,坡角α就越大,坡面就越陡.
如图:坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度.记作i,即i = .
(3) 坡度,坡角
单元小结
(4) 利用解直角三角形的知识解决实际问题的一般过程是:
① 将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
② 根据条件的特点,适当选用锐角三角函数等去解直角三角形;
③ 得到数学问题的答案;
④ 得到实际问题的答案.
单元小结
知识点六 利用三角函数测高
A
C
M
N
①在测点A安置测倾器,测得M的仰角∠MCE=α;
E
②量出测点A到物体底部N的水平距离AN=l;
③量出测倾器的高度AC=a,可求出
MN=ME+EN=l · tanα+a.
α
(1) 测量底部可以到达的物体的高度步骤:
单元小结
考点训练一 锐角三角函数
【例1】如图,在平面直角坐标系内有一点P(3,4),连接OP,求OP与x轴正方向所夹锐角α的正弦值.
解:过点P作PA⊥x轴,P(3,4),
∴A(3,0)
A (0,3)
在△APO中,由勾股定理得
因此
α
单元小结
针对训练
A
B
C
6
1、如图,在Rt△ABC中,∠C=90°,BC=6, sinA= ,求cosA、tanB的值.
解:∵
又
∴
单元小结
2、如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinA的值是________.
【分析】
在Rt△ABC中,∵∠C=90°,AC=4,BC=3,
∴AB=5,
∴sinA=????????????????=????????.
?
????????
?
单元小结
3、一等腰三角形的两边长分别为4cm和6cm,则其底角的余弦值为
__________.
【分析】
①4cm为腰长时,作AD⊥BC于D,
∴BD=CD=3cm,∴cosB=????????;
②4cm为底边时,同理可得:
BD=CD=2cm,∴cosB=????????=????????.
?
????????或????????
?
单元小结
4、如图,已知△????????????中,????????=12,∠????=30°,tan????=247,边????????的垂直平分线分别交????????、????????于点????、????.求线段????????的长.
?
解:过A作AH⊥BC,垂足为点H,如图所示:
在Rt△ABH中,∠B=30°,AB=12,
∴AH=6,BH=63,
在Rt△ACH中,tanC=AHCH=247,
∴CH=74,
∴BC=BH+CH=63+74,
∵DE垂直平分AB,
∴BD=12AB=6,DE⊥AB,
?
单元小结
5、如图,在△ABC中,AD上BC于点D,若AD=6,BC=12,tanC=32,求:
(1)CD的长
(2)cosB的值
?
(1)解:∵AD⊥BC,
∴∠ADC=90°,
∵在Rt△ADC中,tanC=ADCD=32,
∴CD=23AD=4;
(2)解:由(1)得CD=4,
∴BD=BC-CD=8,
在Rt△ABD中,由勾股定理得:AB=AD2+BD2=10,
∴cosB=BDAB=45.
?
单元小结
考点训练二 特殊角的三角函数值
【例2】计算:
(1)tan60°cos30°-3sin245°;
(2)2cos45°-????????tan30°cos30°+sin260°.
?
解:(1)原式=????×????????-3×(????????)2=????????-3×????????=????????-????????=0;
?
解:(2)原式=2×????????-????????×????????×????????+(????????)2=????-????????+????????=????.
?
单元小结
针对训练
1、计算:
(1)cos30°sin45°+sin30°cos45°;
(2)????????????????????°?????????????????????????°?????????????????????????°.
?
解:(1)原式=????????×????????+????????×????????=????????+????????=????+????????;
(2)原式=??????????????????????×????=1??????????????????????=????2.
?
单元小结
2、已知α为锐角,且sin(α-10°)=????????,则α等于_________.
?
【分析】
∵sin(α-10°)=????????,
∴α-10°=60°,
∴α=70°.
?
70°
单元小结
3、在Rt△ABC中,BC=6,AC=2????,∠C=90°,则∠A的度数是_________.
?
【分析】
∵BC=6,AC=2????,∠C=90°,
∴tanA=????????????????=????????????=????,
∴∠A=60°.
?
60°
单元小结
4、若锐角α满足cosα<????????且tanα<????,则α的范围是( )
A.30°<α<45° B.45°<α<60° C.60°<α<90° D.30°<α<60°
?
【分析】
∵α是锐角,∴cosα>0,
∵cosα<????????,∴0<cosα<????????,
又∵cos90°=0,cos45°=????????,
∴45°<α<90°;
?
∵α是锐角,∴tanα>0,
∵tanα<????,∴0<tanα<????,
又∵tan0°=0,tan60°=????,
∴0<α<60°;
故45°<α<60°.
?
B
单元小结
5.已知△????????????中,∠????、∠????都是锐角,且cos?????122+tan?????1=0,
(1)分别求出三个内角度数;
(2)若????????=2,求????????长度.
?
(1)解:∵cos?????122+tan?????1=0
∴cos?????12=0, tan?????1=0
∴cos????=12, tan????=1
∴∠????=60°,∠????=45°
∴∠????=180°?60°?45°=75°;
?
单元小结
(2)解:如图:过点C作CD⊥AB于点D
∵AC=2,∠A=60°
∴∠ACD=30°
∴AD=1,CD=AC2?AD2=22?12=3
∵∠B=45°
∴∠BCD=∠B=45°
∴BD=CD=3
∴AB=AD+BD=1+3.
?
单元小结
6、求下列各式的值:
(1)1-2sin30°cos30° (2)3tan30°-tan45°+2sin60°
(3)(cos230°+sin230°)×tan60°
解:(1)原式
(3)原式
(2)原式
单元小结
考点训练三 解直角三角形
【分析】
∵∠ACB=90°,点D为AB的中点,
∴CD=????????AB=AD,
∴AB=2CD=6,∠ACD=∠A,
∴sin∠ACD=sinA=????????????????=????????=????????.
?
【例3】如图,△ABC中,∠ACB=90°,点D为AB的中点.若BC=4,CD=3,则sin∠ACD=__________.
????????
?
单元小结
针对训练
1、在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边AC的长是____________.
【分析】如图:
∵∠A=35°,
∴cos35°=????????????,
∴AC=m?cos35°.
?
m?cos35°
单元小结
2、在Rt△ACB中,∠C=90°,AB=8,sinA=????????,则BC的长为____________.
?
【分析】如图:
∵sinA=????????,AB=8,
∴sinA=????????????????=????????????=????????,
解得:BC=6.
?
单元小结
3、在△ABC中,AB=4,BC=5,sinB=????????,则△ABC的面积等于____________.
?
【分析】如图,过点A作AD⊥BC,垂足为D,
∵在△ABD中,AB=4,sinB=????????,
∴AD=ABsinB=4×????????=3,
∴△ABC的面积=????????BC?AD=????????×5×3=????????????.
?
单元小结
4、如图,在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是____________.
【分析】如图,过点C作CD⊥AB,交BA的延长线于点D,
∵∠BAC=120°,∴∠CAD=180°-∠BAC=60°,
∵在Rt△ACD中,AC=2,
∴AD=ACcos60°=2×????????=1,CD=ACsin60°=2×????????=????,
∵AB=4,∴BD=AB+AD=4+1=5,
∴在Rt△BDC中,BC=????????????+????????????=????????+????????=2????
∴sinB=????????????????=????????????=????????????????.
?
????????????????
?
单元小结
5、如图,△ABC中,AB=12,BC=15,∠ABC=60°.求tanC的值.
D
解:过点A作AD⊥BC于点D,如图所示:
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵△ABC中,AB=12,
∴AD=AB×sin60°=12×32=63,
BD=AB×cos60°=12×12=6,
∵BC=15,
∴DC=BC?BD=15?6=9,
∴tanC=ADCD=639=233.
?
单元小结
6、如图,已知在△????????????中,????????⊥????????,垂足为点D,????????=2,????????=6,
tan∠????=23,点E是边????????的中点.
(1)求边????????的长;
(2)求∠????????????的正切值.
?
(1)解:∵CD⊥AB,
∴∠ADC=∠CDB=90°,
∴tan∠B=CDDB=23,
∵BD=6,
∴CD=4,
∴AC=CD2+AD2=42+22=25;
?
单元小结
(2)解:过点E作EH⊥AB于点H.
∵CD⊥AB,EH⊥AB,
∴EH∥CD,
∴BECE=BHDH,
∵EC=EB,
∴DH=BH=12BD=3,
∴EH=12CD=2,
∴AH=AD+DH=2+3=5,∴tan∠EAB=EHAH=25.
?
单元小结
考点训练四 三角函数的应用
解:如图,过点E作EF⊥AC于F,则四边形CDEF为矩形.
∴EF=CD,CF=DE=1Om
由题意得∠DAC=∠ADC=45°,∠BEF=30°
设AC=xm,则CD=EF=xm,BF=AC-CF-AB=(x-16)m
在Rt△BEF中,tan∠BEF=
即 ,解得x≈37.8(m)
答:乙楼AC的高度约为37.8m
【例4】如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为30°,已知AB=6m,DE=10m,求乙楼AC的高度(参考数据: 2≈1.41,3≈1.73,精确到0. 1m).
?
单元小结
【例5】已知:如图,斜坡AP的坡度为5:12,坡长AP为13米,在坡顶A处的同一水平面上有一颗大树BC,在斜坡底P处测得该树的树顶B的仰角为45°,在坡顶A处测得该树的树顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)树BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.0)
?
单元小结
(1)坡顶A到地面PQ的距离;
(1)解:过点A作AH⊥PQ,垂足为点H.
∵斜坡AP的坡度为5:12,
∴AHPH=512.
设AH=5k米,则PH=12k米,由勾股定理,得
AP=5k2+12k2=13k米.
∴13k=13,
解得k=1.
∴AH=5.
答:坡顶A到地面PQ的距离为5米.
?
H
单元小结
(2)树BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.0)
?
(2)解:延长BC交PQ于点D.
∵BC⊥AC,AC∥PQ,
∴BD⊥PQ.
∴四边形AHDC是矩形,CD=AH=5,AC=DH.
∵∠BPD=45°,
∴PD=BD.
设BC=x米,则x+5=PH+HD,
由(1)知:PH=12,
∴x+5=12+DH,
∴DH=x?7,
∴AC=DH=x?7.
?
H
D
在Rt△ABC中,tan76°=BCAC,
即xx?7≈4.0,
∴x≈9.
答:树BC的高度约为9米.
?
单元小结
针对训练
1、某人沿着坡度i=1:????的山坡走了150米,则他离地面的高度上升了__________米.
?
【分析】设山坡的坡角为α,
∵山坡的坡度为1:????,
∴tanα=????????=????????,则α=30°,
∴????????×150=75(米).
?
75
单元小结
2、速滑运动受到许多年轻人的喜爱.如图,四边形BCDG是某速滑场馆建造的滑台,已知CD∥EG,滑台的高DG为5米,且坡面BC的坡度为1:1.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为1:????.
(1)求新坡面AC的坡角及AC的长;
?
【分析】(1)如图,过点C作CH⊥BG,垂足为H,
∵新坡面AC的坡度为1:????,
∴tan∠CAH=????????=????????,
∴∠CAH=30°,即新坡面AC的坡角为30°,
∴AC=2CH=10(米);
?
单元小结
(2)原坡面底部BG的正前方10米处(EB=10)是护墙EF,为保证安全,体育管理部门规定,坡面底部至少距护墙7米.请问新的设计方案能否通过,试说明理由(参考数据:????≈1.73)
?
【分析】(2)新的设计方案不能通过,理由如下:
∵坡面BC的坡度为1:1,∴BH=CH=5,
∵tan∠CAH=????????,∴AH=????CH=5????,
∴AB=5????-5,
∴AE=EB-AB=10-(5????-5)=15-5????≈6.35<7,
∴新的设计方案不能通过.
?
单元小结
3、如图,某同学在测量建筑物AB的高度时,在地面的C处测得点A的仰角为30°,向前走60米到达D处,在D处测得点A的仰角为45°,则建筑物AB的高度为__________米.
【分析】
∵∠ADB=45°,∠B=90°,
∴∠BAD=∠ADB=45°,∴AB=BD,
∵tan∠ACB=????????????????,∠ACB=30°,CD=60米,
∴????????=????????????????+????????=????????????????+????????,
解得:AB=30????+30(米).
?
(30????+30)
?
单元小结
4、一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:????≈1.732,结果精确到0.1)?
?
【分析】如图,AC⊥PC,
根据题意,∠APC=60°,∠BPC=45°,AP=20,
在Rt△APC中,∵cos∠APC=????????????????,
∴PC=20?cos60°=10,
∴AC=?????????????????????????=10????,
在△PBC中,∵∠BPC=45°,
∴△PBC为等腰直角三角形,∴BC=PC=10,
∴AB=AC-BC=10????-10≈7.3(海里).
答:它向东航行约7.3海里到达灯塔P南偏西45°方向上的B处.
?
单元小结
5.如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC=74°,坝顶到坝脚的距离AB=6 m.为了提高拦河坝的安全性,现将坡角改为55°,由此,点A需向右平移至点D,请你计算AD
的长(精确到0.1 m).
分析: 将坝顶与坝脚的距离看做直角三角形的斜边,将坡角看做直角三角形的一个锐角,分别作AE,DF垂直于BC,构造直角三角形,求出BE,BF,进而得到AD的长.
单元小结
单元小结
6.如图,一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5 m.在C点上方2 m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果精确到0.01 m)
解:由题意得,BD=5,∠CDB=40°,CE=2m,
在Rt△CBD中, tan∠CDB=????????????????,
∴ BC= BD·tan∠CDB=5tan 40°≈4.195 5≈4.20.
∴BE=BC+CE=4.20+2=6.20,
∴ 在Rt△BED中,DE=????????????+????????????=????????.????????+????????=????????.????????≈7.96.
答:钢缆ED的长度约为7.96 m.
数学(浙教版)
九年级 下册
第1章 解直角三角形
单元小结
知识点一 锐角三角函数
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
如图所示,在Rt△ABC中,∠C=90°,
a,b,c分别是∠A,∠B,∠C的对边.
(1) ∠A的正弦:
∠A的对边
斜边
sin A =
∠A的邻边
斜边
∠A的邻边
∠A的对边
单元小结
知识点二 特殊角的三角函数值
sin30°= ,sin45°= ,sin60°= ;
cos30°= ,cos45°= ,cos60°= ;
tan30°= ,tan45°= ,tan60°= .
1
单元小结
知识点三 解直角三角形
(1) 在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
三边关系: ;
三角关系: ;
边角关系:sinA=cosB= ,cosA=sinB = ,
tanA= ,tanB= .
a2+b2=c2
∠A=90°-∠B
单元小结
(2) 直角三角形可解的条件和解法
?条件:解直角三角形时知道其中的2个元素(至少有一个是边),就可以求出其余的3个未知元素.
?解法:①一边一锐角,先由两锐角互余关系求出另一锐角;知斜边,再用正弦(或余弦)求另两边;知直角边用正切求另一直角边,再用正弦或勾股定理求斜边;②知两边:先用勾股定理求另一边,再用边角关系求锐角;③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.
单元小结
(3) 互余两角的三角函数间的关系
sinα = ,
cosα = ,
sin2α + cos2α = .
tanα · tan(90°-α) = .
cos(90°-α)
sin(90°-α)
1
1
对于sinα与tanα,角度越大,函数值越 ;
对于cosα,角度越大,函数值越 .
大
小
(4) 锐角三角函数的增减性
单元小结
知识点四 借助计算器求锐角三角函数值及锐角
(1) 利用计算器求三角函数值
第二步:输入角度值,
屏幕显示结果.
(也有的计算器是先输入角度再按函数名称键)
第一步:按计算器 键,
sin
tan
cos
单元小结
(2) 利用计算器求锐角的度数
还可以利用 键,进一步得到角的度数.
第二步:输入函数值
屏幕显示答案 (按实际需要进行精确)
方法①:
°'″
2nd F
第一步:按计算器 键,
2nd F
sin
cos
tan
方法②:
第二步:输入锐角函数值
屏幕显示答案 (按实际需要选取精确值).
第一步:按计算器 键,
°'″
2nd F
单元小结
知识点五 三角函数的应用
(1) 仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
单元小结
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角. 如图所示:
30°
45°
B
O
A
东
西
北
南
(2) 方位角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
单元小结
坡面与水平面的夹角叫做坡角,记作α,有 i = tan α.
坡度通常写成1∶m的形式,如i=1∶6.
显然,坡度越大,坡角α就越大,坡面就越陡.
如图:坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度.记作i,即i = .
(3) 坡度,坡角
单元小结
(4) 利用解直角三角形的知识解决实际问题的一般过程是:
① 将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
② 根据条件的特点,适当选用锐角三角函数等去解直角三角形;
③ 得到数学问题的答案;
④ 得到实际问题的答案.
单元小结
知识点六 利用三角函数测高
A
C
M
N
①在测点A安置测倾器,测得M的仰角∠MCE=α;
E
②量出测点A到物体底部N的水平距离AN=l;
③量出测倾器的高度AC=a,可求出
MN=ME+EN=l · tanα+a.
α
(1) 测量底部可以到达的物体的高度步骤:
单元小结
考点训练一 锐角三角函数
【例1】如图,在平面直角坐标系内有一点P(3,4),连接OP,求OP与x轴正方向所夹锐角α的正弦值.
解:过点P作PA⊥x轴,P(3,4),
∴A(3,0)
A (0,3)
在△APO中,由勾股定理得
因此
α
单元小结
针对训练
A
B
C
6
1、如图,在Rt△ABC中,∠C=90°,BC=6, sinA= ,求cosA、tanB的值.
解:∵
又
∴
单元小结
2、如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinA的值是________.
【分析】
在Rt△ABC中,∵∠C=90°,AC=4,BC=3,
∴AB=5,
∴sinA=????????????????=????????.
?
????????
?
单元小结
3、一等腰三角形的两边长分别为4cm和6cm,则其底角的余弦值为
__________.
【分析】
①4cm为腰长时,作AD⊥BC于D,
∴BD=CD=3cm,∴cosB=????????;
②4cm为底边时,同理可得:
BD=CD=2cm,∴cosB=????????=????????.
?
????????或????????
?
单元小结
4、如图,已知△????????????中,????????=12,∠????=30°,tan????=247,边????????的垂直平分线分别交????????、????????于点????、????.求线段????????的长.
?
解:过A作AH⊥BC,垂足为点H,如图所示:
在Rt△ABH中,∠B=30°,AB=12,
∴AH=6,BH=63,
在Rt△ACH中,tanC=AHCH=247,
∴CH=74,
∴BC=BH+CH=63+74,
∵DE垂直平分AB,
∴BD=12AB=6,DE⊥AB,
?
单元小结
5、如图,在△ABC中,AD上BC于点D,若AD=6,BC=12,tanC=32,求:
(1)CD的长
(2)cosB的值
?
(1)解:∵AD⊥BC,
∴∠ADC=90°,
∵在Rt△ADC中,tanC=ADCD=32,
∴CD=23AD=4;
(2)解:由(1)得CD=4,
∴BD=BC-CD=8,
在Rt△ABD中,由勾股定理得:AB=AD2+BD2=10,
∴cosB=BDAB=45.
?
单元小结
考点训练二 特殊角的三角函数值
【例2】计算:
(1)tan60°cos30°-3sin245°;
(2)2cos45°-????????tan30°cos30°+sin260°.
?
解:(1)原式=????×????????-3×(????????)2=????????-3×????????=????????-????????=0;
?
解:(2)原式=2×????????-????????×????????×????????+(????????)2=????-????????+????????=????.
?
单元小结
针对训练
1、计算:
(1)cos30°sin45°+sin30°cos45°;
(2)????????????????????°?????????????????????????°?????????????????????????°.
?
解:(1)原式=????????×????????+????????×????????=????????+????????=????+????????;
(2)原式=??????????????????????×????=1??????????????????????=????2.
?
单元小结
2、已知α为锐角,且sin(α-10°)=????????,则α等于_________.
?
【分析】
∵sin(α-10°)=????????,
∴α-10°=60°,
∴α=70°.
?
70°
单元小结
3、在Rt△ABC中,BC=6,AC=2????,∠C=90°,则∠A的度数是_________.
?
【分析】
∵BC=6,AC=2????,∠C=90°,
∴tanA=????????????????=????????????=????,
∴∠A=60°.
?
60°
单元小结
4、若锐角α满足cosα<????????且tanα<????,则α的范围是( )
A.30°<α<45° B.45°<α<60° C.60°<α<90° D.30°<α<60°
?
【分析】
∵α是锐角,∴cosα>0,
∵cosα<????????,∴0<cosα<????????,
又∵cos90°=0,cos45°=????????,
∴45°<α<90°;
?
∵α是锐角,∴tanα>0,
∵tanα<????,∴0<tanα<????,
又∵tan0°=0,tan60°=????,
∴0<α<60°;
故45°<α<60°.
?
B
单元小结
5.已知△????????????中,∠????、∠????都是锐角,且cos?????122+tan?????1=0,
(1)分别求出三个内角度数;
(2)若????????=2,求????????长度.
?
(1)解:∵cos?????122+tan?????1=0
∴cos?????12=0, tan?????1=0
∴cos????=12, tan????=1
∴∠????=60°,∠????=45°
∴∠????=180°?60°?45°=75°;
?
单元小结
(2)解:如图:过点C作CD⊥AB于点D
∵AC=2,∠A=60°
∴∠ACD=30°
∴AD=1,CD=AC2?AD2=22?12=3
∵∠B=45°
∴∠BCD=∠B=45°
∴BD=CD=3
∴AB=AD+BD=1+3.
?
单元小结
6、求下列各式的值:
(1)1-2sin30°cos30° (2)3tan30°-tan45°+2sin60°
(3)(cos230°+sin230°)×tan60°
解:(1)原式
(3)原式
(2)原式
单元小结
考点训练三 解直角三角形
【分析】
∵∠ACB=90°,点D为AB的中点,
∴CD=????????AB=AD,
∴AB=2CD=6,∠ACD=∠A,
∴sin∠ACD=sinA=????????????????=????????=????????.
?
【例3】如图,△ABC中,∠ACB=90°,点D为AB的中点.若BC=4,CD=3,则sin∠ACD=__________.
????????
?
单元小结
针对训练
1、在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边AC的长是____________.
【分析】如图:
∵∠A=35°,
∴cos35°=????????????,
∴AC=m?cos35°.
?
m?cos35°
单元小结
2、在Rt△ACB中,∠C=90°,AB=8,sinA=????????,则BC的长为____________.
?
【分析】如图:
∵sinA=????????,AB=8,
∴sinA=????????????????=????????????=????????,
解得:BC=6.
?
单元小结
3、在△ABC中,AB=4,BC=5,sinB=????????,则△ABC的面积等于____________.
?
【分析】如图,过点A作AD⊥BC,垂足为D,
∵在△ABD中,AB=4,sinB=????????,
∴AD=ABsinB=4×????????=3,
∴△ABC的面积=????????BC?AD=????????×5×3=????????????.
?
单元小结
4、如图,在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是____________.
【分析】如图,过点C作CD⊥AB,交BA的延长线于点D,
∵∠BAC=120°,∴∠CAD=180°-∠BAC=60°,
∵在Rt△ACD中,AC=2,
∴AD=ACcos60°=2×????????=1,CD=ACsin60°=2×????????=????,
∵AB=4,∴BD=AB+AD=4+1=5,
∴在Rt△BDC中,BC=????????????+????????????=????????+????????=2????
∴sinB=????????????????=????????????=????????????????.
?
????????????????
?
单元小结
5、如图,△ABC中,AB=12,BC=15,∠ABC=60°.求tanC的值.
D
解:过点A作AD⊥BC于点D,如图所示:
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵△ABC中,AB=12,
∴AD=AB×sin60°=12×32=63,
BD=AB×cos60°=12×12=6,
∵BC=15,
∴DC=BC?BD=15?6=9,
∴tanC=ADCD=639=233.
?
单元小结
6、如图,已知在△????????????中,????????⊥????????,垂足为点D,????????=2,????????=6,
tan∠????=23,点E是边????????的中点.
(1)求边????????的长;
(2)求∠????????????的正切值.
?
(1)解:∵CD⊥AB,
∴∠ADC=∠CDB=90°,
∴tan∠B=CDDB=23,
∵BD=6,
∴CD=4,
∴AC=CD2+AD2=42+22=25;
?
单元小结
(2)解:过点E作EH⊥AB于点H.
∵CD⊥AB,EH⊥AB,
∴EH∥CD,
∴BECE=BHDH,
∵EC=EB,
∴DH=BH=12BD=3,
∴EH=12CD=2,
∴AH=AD+DH=2+3=5,∴tan∠EAB=EHAH=25.
?
单元小结
考点训练四 三角函数的应用
解:如图,过点E作EF⊥AC于F,则四边形CDEF为矩形.
∴EF=CD,CF=DE=1Om
由题意得∠DAC=∠ADC=45°,∠BEF=30°
设AC=xm,则CD=EF=xm,BF=AC-CF-AB=(x-16)m
在Rt△BEF中,tan∠BEF=
即 ,解得x≈37.8(m)
答:乙楼AC的高度约为37.8m
【例4】如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为30°,已知AB=6m,DE=10m,求乙楼AC的高度(参考数据: 2≈1.41,3≈1.73,精确到0. 1m).
?
单元小结
【例5】已知:如图,斜坡AP的坡度为5:12,坡长AP为13米,在坡顶A处的同一水平面上有一颗大树BC,在斜坡底P处测得该树的树顶B的仰角为45°,在坡顶A处测得该树的树顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)树BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.0)
?
单元小结
(1)坡顶A到地面PQ的距离;
(1)解:过点A作AH⊥PQ,垂足为点H.
∵斜坡AP的坡度为5:12,
∴AHPH=512.
设AH=5k米,则PH=12k米,由勾股定理,得
AP=5k2+12k2=13k米.
∴13k=13,
解得k=1.
∴AH=5.
答:坡顶A到地面PQ的距离为5米.
?
H
单元小结
(2)树BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.0)
?
(2)解:延长BC交PQ于点D.
∵BC⊥AC,AC∥PQ,
∴BD⊥PQ.
∴四边形AHDC是矩形,CD=AH=5,AC=DH.
∵∠BPD=45°,
∴PD=BD.
设BC=x米,则x+5=PH+HD,
由(1)知:PH=12,
∴x+5=12+DH,
∴DH=x?7,
∴AC=DH=x?7.
?
H
D
在Rt△ABC中,tan76°=BCAC,
即xx?7≈4.0,
∴x≈9.
答:树BC的高度约为9米.
?
单元小结
针对训练
1、某人沿着坡度i=1:????的山坡走了150米,则他离地面的高度上升了__________米.
?
【分析】设山坡的坡角为α,
∵山坡的坡度为1:????,
∴tanα=????????=????????,则α=30°,
∴????????×150=75(米).
?
75
单元小结
2、速滑运动受到许多年轻人的喜爱.如图,四边形BCDG是某速滑场馆建造的滑台,已知CD∥EG,滑台的高DG为5米,且坡面BC的坡度为1:1.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为1:????.
(1)求新坡面AC的坡角及AC的长;
?
【分析】(1)如图,过点C作CH⊥BG,垂足为H,
∵新坡面AC的坡度为1:????,
∴tan∠CAH=????????=????????,
∴∠CAH=30°,即新坡面AC的坡角为30°,
∴AC=2CH=10(米);
?
单元小结
(2)原坡面底部BG的正前方10米处(EB=10)是护墙EF,为保证安全,体育管理部门规定,坡面底部至少距护墙7米.请问新的设计方案能否通过,试说明理由(参考数据:????≈1.73)
?
【分析】(2)新的设计方案不能通过,理由如下:
∵坡面BC的坡度为1:1,∴BH=CH=5,
∵tan∠CAH=????????,∴AH=????CH=5????,
∴AB=5????-5,
∴AE=EB-AB=10-(5????-5)=15-5????≈6.35<7,
∴新的设计方案不能通过.
?
单元小结
3、如图,某同学在测量建筑物AB的高度时,在地面的C处测得点A的仰角为30°,向前走60米到达D处,在D处测得点A的仰角为45°,则建筑物AB的高度为__________米.
【分析】
∵∠ADB=45°,∠B=90°,
∴∠BAD=∠ADB=45°,∴AB=BD,
∵tan∠ACB=????????????????,∠ACB=30°,CD=60米,
∴????????=????????????????+????????=????????????????+????????,
解得:AB=30????+30(米).
?
(30????+30)
?
单元小结
4、一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:????≈1.732,结果精确到0.1)?
?
【分析】如图,AC⊥PC,
根据题意,∠APC=60°,∠BPC=45°,AP=20,
在Rt△APC中,∵cos∠APC=????????????????,
∴PC=20?cos60°=10,
∴AC=?????????????????????????=10????,
在△PBC中,∵∠BPC=45°,
∴△PBC为等腰直角三角形,∴BC=PC=10,
∴AB=AC-BC=10????-10≈7.3(海里).
答:它向东航行约7.3海里到达灯塔P南偏西45°方向上的B处.
?
单元小结
5.如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC=74°,坝顶到坝脚的距离AB=6 m.为了提高拦河坝的安全性,现将坡角改为55°,由此,点A需向右平移至点D,请你计算AD
的长(精确到0.1 m).
分析: 将坝顶与坝脚的距离看做直角三角形的斜边,将坡角看做直角三角形的一个锐角,分别作AE,DF垂直于BC,构造直角三角形,求出BE,BF,进而得到AD的长.
单元小结
单元小结
6.如图,一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5 m.在C点上方2 m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果精确到0.01 m)
解:由题意得,BD=5,∠CDB=40°,CE=2m,
在Rt△CBD中, tan∠CDB=????????????????,
∴ BC= BD·tan∠CDB=5tan 40°≈4.195 5≈4.20.
∴BE=BC+CE=4.20+2=6.20,
∴ 在Rt△BED中,DE=????????????+????????????=????????.????????+????????=????????.????????≈7.96.
答:钢缆ED的长度约为7.96 m.
