第5章 一次函数 基础卷(含解析）

中小学教育资源及组卷应用平台
一次函数单元基础卷(含解析）
一、单选题
1．关于一次函数 ，下列说法中正确的是（　　）
A．y随x的增大而增大 B．图象经过第一、二、三象限
C．与x轴交于 D．与y轴交于
2．已知一次函数y=kx+b中，x取不同值时，y对应的值列表如下：
x … -m2-1 2 3 …
y … -1 0 n2+1 …
则不等式kx+b＞0（其中k，b，m，n为常数）的解集为（　　）
A．x＞2 B．x＞3 C．x＜2 D．无法确定
3．直线上有三个点，则的大小关系是（　　）
A． B． C． D．
4．已知点(k，b)为第四象限内的点，则一次函数y=kx+b的图象大致是（　　）
A．B．C． D．
5．正比例函数和一次函数（k为常数，且）的图象交于点，则关于x的不等式的解集为（　　）
A． B． C． D．
6．正比例函数y＝2x的图象经过点A（3，m），B（﹣2，n），则m与n的大小关系是（　　）
A．m＞n B．m＜n C．m＝n D．无法确定
7．已知一次函数的图象经过第一，二，三象限，且与x轴交于点（－2，0），则不等式的解是（　　）
A． B． C． D．
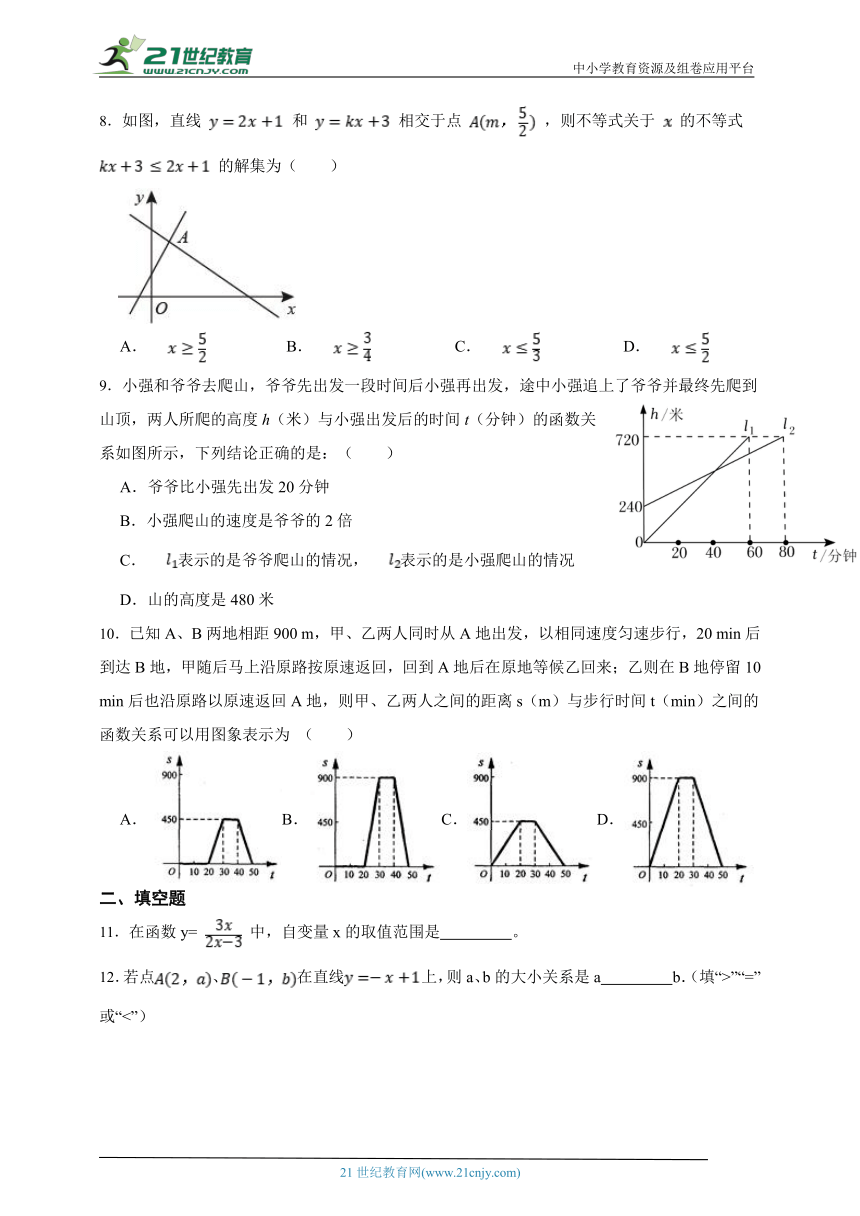
8．如图，直线 和 相交于点 ，则不等式关于 的不等式 的解集为（　　）
A． B． C． D．
9．小强和爷爷去爬山，爷爷先出发一段时间后小强再出发，途中小强追上了爷爷并最终先爬到山顶，两人所爬的高度h（米）与小强出发后的时间t（分钟）的函数关系如图所示，下列结论正确的是：（　　）
A．爷爷比小强先出发20分钟
B．小强爬山的速度是爷爷的2倍
C．表示的是爷爷爬山的情况，表示的是小强爬山的情况
D．山的高度是480米
10．已知A、B两地相距900 m，甲、乙两人同时从A地出发，以相同速度匀速步行，20 min后到达B地，甲随后马上沿原路按原速返回，回到A地后在原地等候乙回来；乙则在B地停留10 min后也沿原路以原速返回A地，则甲、乙两人之间的距离s（m）与步行时间t（min）之间的函数关系可以用图象表示为 （　　）
A．B．C．D．
二、填空题
11．在函数y= 中，自变量x的取值范围是　 　。
12．若点、在直线上，则a、b的大小关系是a　 　b．（填“>”“=”或“<”）
13．如图：点在直线上，则不等式关于的解集是　 　．
14． 在平面直角坐标系中，若函数的图象经过点和，则的值为　 　 ．
15．已知一次函数，当时，的最大值等于　 　．
16．直线与相交于点，则关于x，y的二元一次方程组的解为　 　.
三、解答题
17．在 中，当 时， ，当 时， ，求 和 的值．
18．如图，在平面直角坐标系中有A、B、C、D四个点，它们的坐标分别为、、、．
（1）若y是x的正比例函数，请从A、B、C、D四个点中选择一个合适的点代入解析式中，并求出此时的函数解析式；
（2）作直线AC，，若直线，相交于点E，请求出点E的坐标．
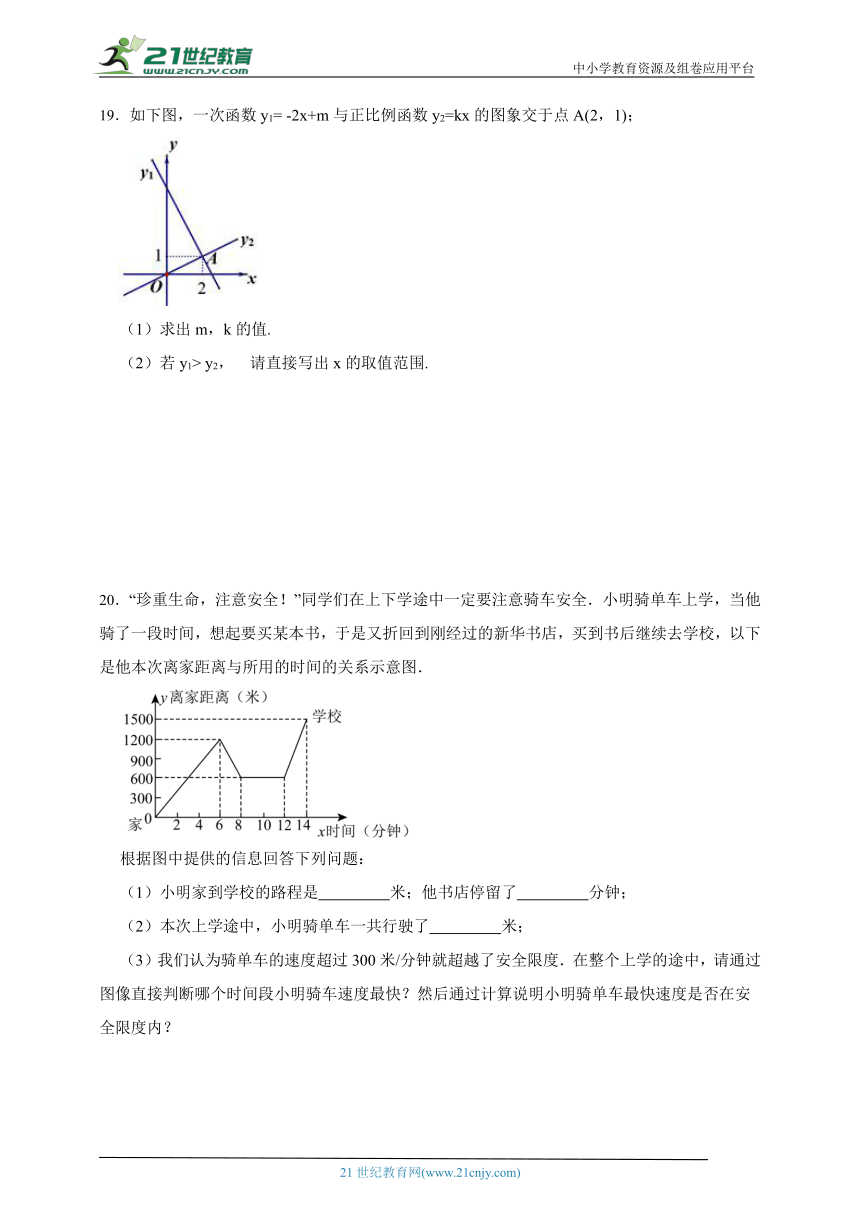
19．如下图，一次函数y1= -2x+m与正比例函数y2=kx的图象交于点A(2，1)；
（1）求出m，k的值.
（2）若y1> y2， 请直接写出x的取值范围.
20．“珍重生命，注意安全！”同学们在上下学途中一定要注意骑车安全．小明骑单车上学，当他骑了一段时间，想起要买某本书，于是又折回到刚经过的新华书店，买到书后继续去学校，以下是他本次离家距离与所用的时间的关系示意图．
根据图中提供的信息回答下列问题：
（1）小明家到学校的路程是　 　米；他书店停留了　 　分钟；
（2）本次上学途中，小明骑单车一共行驶了　 　米；
（3）我们认为骑单车的速度超过300米/分钟就超越了安全限度．在整个上学的途中，请通过图像直接判断哪个时间段小明骑车速度最快？然后通过计算说明小明骑单车最快速度是否在安全限度内？
21．某校餐厅计划购买12张餐桌和一批餐椅，现从甲、乙两商场了解到：同一型号的餐桌报价每张均为200元，餐椅报价每把均为50元．甲商场称：每购买一张餐桌赠送一把餐椅；乙商场规定：所有餐桌椅均按报价的八五折销售．那么，学校应如何购买更优惠？
22．如图，直线：与直线：相交于点．
（1）求m、b的值；
（2）请直接写出关于x、y的方程组的解　 　；
（3）请直接写出关于x的不等式组的解集　 　．
23．两个一次函数的图象如图所示，
（1）分别求出两个一次函数的解析式；
（2）求出两个一次函数图象的交点C坐标；
（3）求这两条直线与y轴围成△ABC的面积．
24．心理学家发现，学生对概念的接受能力y与提出概念所用的时间x（单位：分）之间有如下关系：（其中0≤x≤30）
提出概念所 用时间（x） 2 5 7 10 12 13 14 17 20
对概念的接受能力（y） 47.8 53.5 56.3 59.0 59.8 59.9 59.8 58.3 55.0
（1）上表中反映了哪两个变量之间的关系？
（2）当提出概念所用时间是5分钟时，学生的接受能力是多少？
（3）根据表格中的数据，你认为提出概念几分钟时，学生的接受能力最强？
（4）从表中可知，当时间x在什么范围内，学生的接受能力逐步增强？当时间x在什么范围内，学生的接受能力逐步降低？
答案解析部分
1．【答案】A
【解析】【解答】 一次函数 中的 ，
y随x的增大而增大，则选项A正确；
一次函数 中的 ， ，
此函数的图象经过第一、三、四象限，则选项B错误；
对于一次函数 ，
当 时， ，解得 ，
即与x轴交于 ，选项C错误；
当 时， ，
即与y轴交于 ，选项D错误；
故答案为：A.
【分析】由k=1＞0可知直线经过第一、三象限，且y随x的增大而增大；由b=-2＜0可知直线交于y轴的负半轴，其交点为（0，-2），即直线经过第一、三、四象限，把y=0代入解析式计算可得直线与x轴的交点坐标为（2,0）.
2．【答案】A
【解析】【解答】由表格可得：x=2时，y=0，由n2+1＞0，
则x＞2时，不等式kx+b＞0（其中k，b，m，n为常数）．
故答案为：A．
【分析】直接利用已知表格中数据得出：x=2时，y=0，由n2+1＞0，知次函数y随x的增大而增大，进而得出不等式的解集。
3．【答案】C
【解析】【解答】 由，3＞0可知y随x的增大而增大，∵-2.3＜-1.3＜2.7，∴，故C符合题意.
故选C.
【分析】本题考查一次函数的性质，由y=kx+b得，当k＞0时，y随x的增大而增大，当k＜0时，y随x的增大而减小.
4．【答案】B
【解析】【解答】第四象限的坐标，横坐标＞0，纵坐标＜0，所以k＞0，b＜0，
所以对于一次函数而言，k＞0，y随x的增大而增大，
b＜0，与y轴的交点＜0，
所以图像是B
故答案为：B
【分析】根据象限与坐标的关系，判断大小，再利用一次函数系数与图像的关系可找到正确图像。
5．【答案】C
【解析】【解答】解：将A（m，3）代入y=2x中可得3=2m，
解得m=，
∴A（，3），
∴2x故答案为：C.
【分析】将A（m，3）代入y=2x中求出m的值，得到点A的坐标，然后根据一次函数的图象可得不等式的解集.
6．【答案】A
【解析】【解答】 正比例函数 中的一次项系数大于0，
随 的增大而增大，
又 点 在正比例函数 的图象上，且 ，
，
故答案为：A．
【分析】根据正比例函数中K的值，确定函数的增减性，在比较M、N个大小即可。
7．【答案】A
【解析】【解答】解：∵一次函数y=kx+b的图象经过一、二、三象限，则函数y随x的增大而增大，
∴k>0.
∵一次函数y=kx+b的图象与x轴交于点（-2，0），即当x=-2时，y=0，
∴关于x的不等式kx+b>0的解集是x>-2.
故答案为：A.
【分析】由题意可得k>0，由图象过点（-2，0）可得当x=-2时，y=0，据此不难得到不等式kx+b>0的解集.
8．【答案】B
【解析】【解答】解：∵直线y=2x+1和y=kx+3相交于点 ，
∴ =2m+1，解得m= ，
∴A（ ， ），
由函数图象可知，当x≥ 时，直线y=2x+1的图象不在直线y=kx+3的图象的下方，
∵当x≥ 时，kx+3≤2x+1．
故答案为：B．
【分析】先求出点A的坐标，再结合图象，函数值大的图象在上方的原则求解即可。
9．【答案】B
【解析】【解答】解：由题意得山的高度为720米，故D错误；
∵爷爷先出发一段时间后小强再出发，
∴表示的是小强爬山的情况，表示的是爷爷爬山的情况，故C错误；
爷爷的爬山速度为，
小强的爬山速度为，
∴小强的爬山速度是爷爷的两倍，故B正确；
∵240÷6=40（min），
∴爷爷比小强先出发40分钟，故A错误；
故答案为：B
【分析】先根据函数的图象即可判断山的高度，再结合题意即可判断C选项，再运用速度=路程÷时间分别求出小强和爷爷的爬山速度即可，最后再运用时间=路程÷速度即可求出爷爷比小强早出发的时间。
10．【答案】A
【解析】【解答】解：∵甲乙二人乙相同速度匀速步行20 min后从A地到达B地，
∴二人步行的距离为900÷2=450m，
0-20min时，二人同行，距离为0，
20-30min时，甲返回，乙停留在B 地，距离S从0到450m ，
30-40min时，甲继续返回，乙也返回，二人之间的距离保持450m不变，
40-50min时，甲在A地等乙，乙返回，距离S从450到0m，
纵观各选项，只有A选项图象符合.
故答案为：A .
【分析】由题意可得：二人步行的距离为900÷2=450m，0-20min时，二人同行，距离为0；20-30min时，距离S从0到450m；30-40min时，二人之间的距离保持450m不变；40-50min时，距离S从450到0m，据此判断.
11．【答案】x≠
【解析】【解答】解：∵ 函数y=
∴自变量x的取值范围为：2x-3≠0，即x≠
故答案为：x≠
【分析】此函数解析式中，含自变量的式子是分式，因此分母≠0，建立关于x的不等式，求解即可。
12．【答案】<
【解析】【解答】解：∵中，k＝ 1＜0，
∴y随x的增大而减小．
又∵2＞ 1，
∴a＜b．
故答案为：＜．
【分析】先求出y随x的增大而减小，再比较大小即可。
13．【答案】
【解析】【解答】
方法1：
点在直线上∴ y=3时，x＝-2
由图分析可知，当，x≤-2
方法2：
∵ 点在直线上
∴ -2k+b=3
∴ b=3+2k
∴ kx+3+2k≥3
∴ kx+2k≥0
∴ k（x+2）≥0
∴ x+2≤0
即 x≤-2
【分析】本题考查一次函数与一元一次不等式的关系。 利用一次函数图象解一元一次不等式要先找线，由y的范围确定图象，对应的横坐标x的取值范围就是一元一次不等式的解集。或者点在函数上，得到b的代数式，再代入求不等式的解集也可。
14．【答案】4
【解析】【解答】由题意，代入（-4，2）到函数解析式
得-4k=2
解得k=
函数解析式为
代入（m，-2），
解得m=4
故填：4
【分析】根据给定的A点坐标，求出函数解析式；再代入点B的坐标，可求m值。
15．【答案】5
【解析】【解答】解：∵k=2＞0，
∴y随x的增大而增大，
∵-2＜x＜2，
∴当x=2时，y=2×2+1=5，
∴y的最大值为5.
故答案为：5.
【分析】根据一次函数的性质得出y随x的增大而增大，得出当x=2时，y的值最大，把x=2代入y=2x+1求出y的值，即可得出答案.
16．【答案】
【解析】【解答】解：∵直线与相交于点，
∴关于x，y的二元一次方程组的解为，
故答案为：.
【分析】两一次函数图象的交点坐标即为对应的二元一次方程组的解，据此解答.
17．【答案】解：当 时， ，当 时，
解得：
【解析】【分析】把已知 的值代入 得到关于 的方程组，解得 的值．
18．【答案】（1）解：若选C：设正比例函数解析式为，
将点代入得，，
∴正比例函数的解析式为；
若选D：设正比例函数解析式为，
将点代入得，，
∴正比例函数的解析式为；
（2）解：设直线的解析式为：
将，分别代入得：
，解得：
∴直线为：.
同理，求得直线为：
解方程组得：
所以点E的坐标为．
【解析】【分析】（1）这里可以选择C点或D点，根据待定系数法即可求解.
（2）利用待定系数法求出AC、BD的解析式，由AC、BD的解析式组成方程组，求出其解即为E点的坐标.
19．【答案】（1）解：∵ 一次函数y1= -2x+m与正比例函数y2=kx的图象交于点A(2，1)
∴-4+m=1，2k=1
解之：m=5，；
（2）
【解析】【解答】解：（2）∵一次函数y1= -2x+m与正比例函数y2=kx的图象交于点A(2，1)
当x＜2时，直线y1= -2x+5m高于直线 y2=x ，即y1> y2.
【分析】（1）根据已知条件可知，将点A的坐标分别代入两函数解析式，建立关于m，k的方程组，解方程组的解，可得到m，k的值。
（2）观察函数图象，由两函数的交点坐标可得到y1> y2时的自变量x的取值范围。
20．【答案】（1）1500；4
（2）2700
（3）解：由图像可知：0～6分钟时，平均速度米/分，
6～8分钟时，平均速度米/分，
12～14分钟时，平均速度米/分，
所以，12～14分钟时速度最快，不在安全限度内．
【解析】【解答】解：（1）由图像可知：小明家到学校的距离为1500米，他在书店停留了：12-8=4（分钟）
故答案为：第1空、1500
第2空、4
（2） 小明骑单车一共行驶了 1200+（1200-600）+（1500-600）=2700（米）
故答案为：2700
【分析】（1）根据图像的纵坐标与横坐标即可求出答案；
（2）根据图像的纵坐标得到相应的路程，即可求出答案；
（3）根据图像的纵坐标得到相应的路程，根据横坐标可得时间，依据路程与时间的关系可得速度，即可求出答案。
21．【答案】解：设学校购买12张餐桌和 把餐椅，到购买甲商场的费用为 元，到乙商场购买的费用为 元，则有
当 ，即 时，
答：当学校购买的餐椅少于32把时，到甲商场购买更优惠。
【解析】【分析】 设学校购买12张餐桌和 把餐椅，到购买甲商场的费用为 元，到乙商场购买的费用为 元，根据购买的费用=购买桌子的数量×桌的单价+购买椅子的数量×椅子的单价，分别表示出y1与y2的关系式;分三种情况①当y1＞y2，②y1=y2，③y1＜y2时讨论即得.
22．【答案】（1）解：解：∵直线与相交于点，
∴；
将点代入得：，
∴
（2）
（3）
【解析】【解答】解：（2）由（1）知： 直线：与直线：相交于点 P（1，2）
则 关于x、y的方程组的解是
（3） 由（1）知：关于x的不等式组 可整理为：
由①得：x＞-1
由②得：x＜3
∴ 不等式的解集是：-1＜x＜3
【分析】本题考查一次函数的交点和方程组、不等式组的联系。正确理解它们之间的关系是解题关键。
23．【答案】（1）解：设l1的解析式为y=k1x+b1，l2的解析式为y=k2x+b2，
把（﹣2，0），（0，﹣3）代入l1，（4，0），（0，1）代入l2得， ， ，
解得： ， ．
所以l1的解析式为y=﹣ x﹣3，l2的解析式为y=﹣ x+1；
（2）解：联立方程组 ，解得： ，
所以两个一次函数图象的交点坐标（ ， ）
（3）解：三角形的面积= =
【解析】【分析】（1）将坐标代入解析式，待定系数法求出两条直线的解析式。（2）求解出二元一次方程组，解出x、y的值，即为交点坐标。（3）利用A、B、C三点坐标，得到三角形的底与高，求出面积。
24．【答案】解：（1）提出概念所用的时间和对概念接受能力y两个变量；
（2）当时间是5分钟时，学生的接受能力是53.5；
（3）当提出概念13分钟时，学生的接受能力最强59.9；
（4）当2≤x≤13时，y值逐渐增大，学生的接受能力逐步增强；
当13≤x≤20时，y值逐渐减小，学生的接受能力逐步降低．
【解析】【分析】（1）根据题意得出是学生对概念的接受能力y与提出概念所用的时间x（单位：分）之间关系；
（2）利用图表中数据得出答案；
（3）利用图表中数据得出答案；
（4）利用图表中数据得出答案．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)