浙教版数学八年级下册1.3.3二次根式的实际应用 素养提升练习(含解析)
文档属性
| 名称 | 浙教版数学八年级下册1.3.3二次根式的实际应用 素养提升练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 124.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 00:00:00 | ||
图片预览



文档简介
第1章 二次根式
1.3 二次根式的运算
第3课时 二次根式的实际应用
基础过关全练
知识点1 坡比(坡度)问题
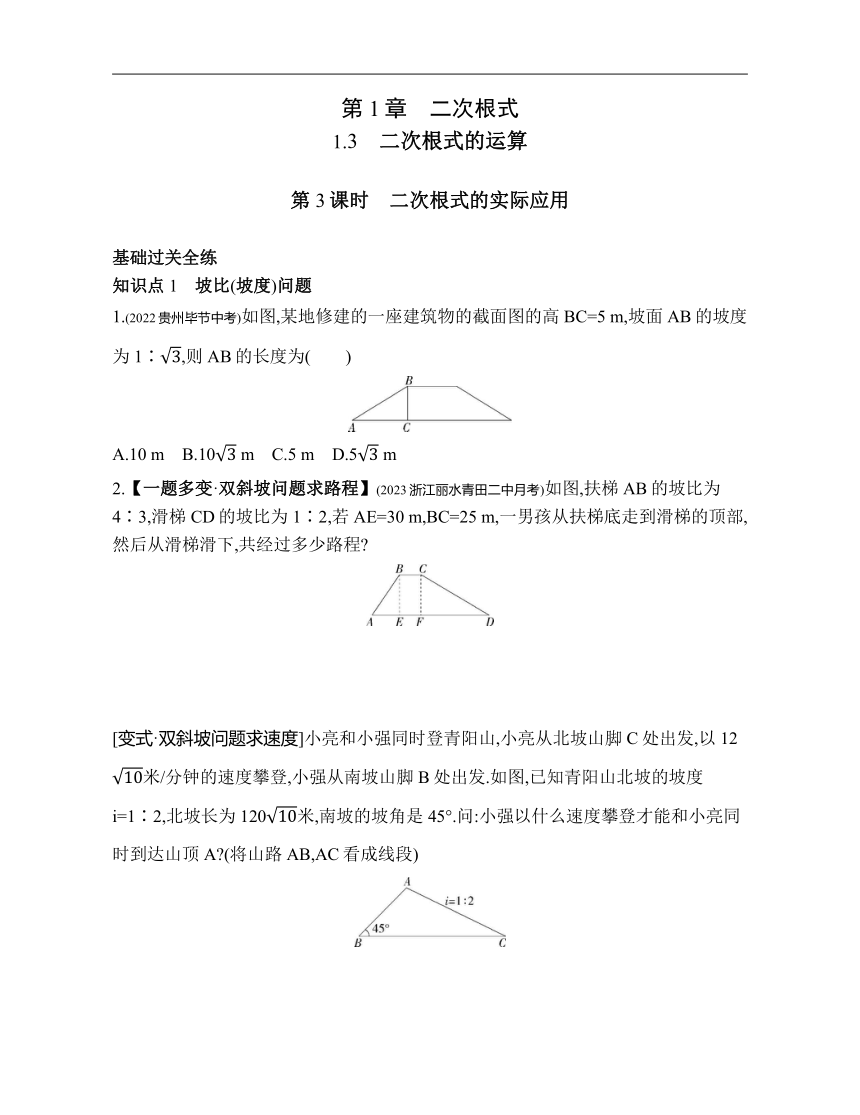
1.(2022贵州毕节中考)如图,某地修建的一座建筑物的截面图的高BC=5 m,坡面AB的坡度为1∶,则AB的长度为( )
A.10 m B.10 m C.5 m D.5 m
2.【一题多变·双斜坡问题求路程】(2023浙江丽水青田二中月考)如图,扶梯AB的坡比为4∶3,滑梯CD的坡比为1∶2,若AE=30 m,BC=25 m,一男孩从扶梯底走到滑梯的顶部,然后从滑梯滑下,共经过多少路程
[变式·双斜坡问题求速度]小亮和小强同时登青阳山,小亮从北坡山脚C处出发,以12 米/分钟的速度攀登,小强从南坡山脚B处出发.如图,已知青阳山北坡的坡度i=1∶2,北坡长为120米,南坡的坡角是45°.问:小强以什么速度攀登才能和小亮同时到达山顶A (将山路AB,AC看成线段)
知识点2 几何图形问题
3.【分类讨论思想】一个等腰三角形的两边长分别为2,3,则这个三角形的周长为( )
A.3+4 B.6+2
C.6+4 D.3+4或6+2
4.若一个三角形的面积为12,一边长为+1,则该边上的高为( )
A.12+12 B.24-24
C.12-12 D.24+24
5.【新独家原创】若平行四边形相邻的两边长如图所示,则它的周长为 cm.
能力提升全练
6.如图,在离地面高5 m处引拉线固定电线杆,电线杆与地面垂直,拉线与地面成60°角,则拉线AC的长是( )
A.10 m B. m C. m D.5 m
7.如图,已知鱼竿AC的长为6 m,露出水面的渔线BC的长为3 m,钓鱼者想看看鱼钩的情况,他把鱼竿AC转动到AC'的位置,此时露出水面的渔线B'C'的长为 m,则BB'的长为( )
A. m B.2 m C. m D.2 m
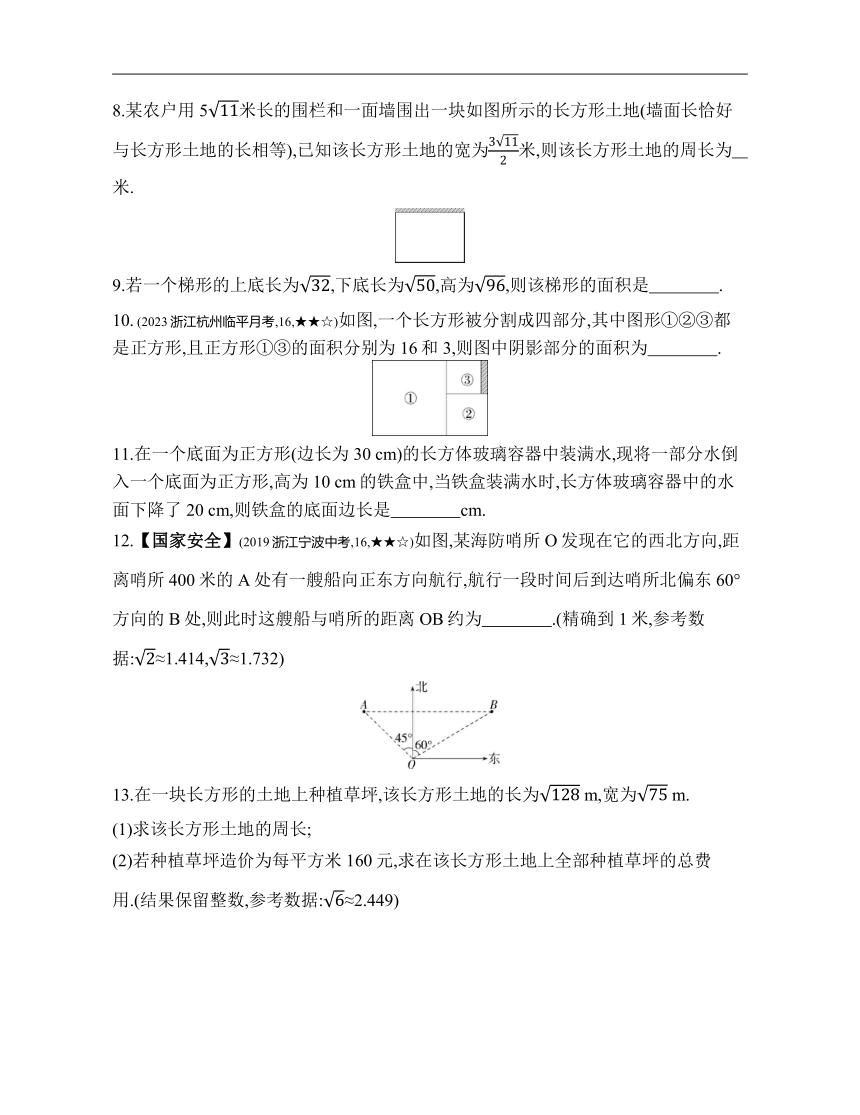
8.某农户用5米长的围栏和一面墙围出一块如图所示的长方形土地(墙面长恰好与长方形土地的长相等),已知该长方形土地的宽为米,则该长方形土地的周长为 米.
9.若一个梯形的上底长为,下底长为,高为,则该梯形的面积是 .
10. (2023浙江杭州临平月考,16,★★☆)如图,一个长方形被分割成四部分,其中图形①②③都是正方形,且正方形①③的面积分别为16和3,则图中阴影部分的面积为 .
11.在一个底面为正方形(边长为30 cm)的长方体玻璃容器中装满水,现将一部分水倒入一个底面为正方形,高为10 cm的铁盒中,当铁盒装满水时,长方体玻璃容器中的水面下降了20 cm,则铁盒的底面边长是 cm.
12.【国家安全】(2019浙江宁波中考,16,★★☆)如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为 .(精确到1米,参考数据:≈1.414,≈1.732)
13.在一块长方形的土地上种植草坪,该长方形土地的长为 m,宽为 m.
(1)求该长方形土地的周长;
(2)若种植草坪造价为每平方米160元,求在该长方形土地上全部种植草坪的总费用.(结果保留整数,参考数据:≈2.449)
素养探究全练
14.【运算能力】在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了利用三角形的三条边的长来求面积.我国南宋著名的数学家秦九韶提出了“三斜求积术”(利用三角形三边长求三角形面积的方法),简称为秦九韶公式.在海伦的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,故我国称这个公式为海伦-秦九韶公式.它的表述如下:三角形三边长分别为a、b、c,则三角形的面积S=(其中p为半周长,即周长的一半).
(1)求三边长分别为3、6、7的三角形的面积;
(2)四边形ABCD中,AB=3,BC=4,CD=7,AD=6,∠B=90°,求四边形ABCD的面积.
第1章 二次根式
1.3 二次根式的运算
第3课时 二次根式的实际应用
答案全解全析
基础过关全练
1.A ∵坡面AB的坡度为1∶,BC=5 m,∴=,∴AC=5 m,∴AB===10(m).
2 解析 ∵扶梯AB的坡比为4∶3,AE=30 m,
∴BE=40 m,
∴AB===50(m),
∵CF=BE=40 m,滑梯CD的坡比为1∶2,
∴FD=2CF=2×40=80(m),
∴CD===40(m),
∴经过的路程=AB+BC+CD=50+25+40=(75+40) m.
[变式]解析 如图,过点A作AD⊥BC于D.
在Rt△ACD中,i==,
设AD=x米,则CD=2x米,
根据勾股定理得AD2+CD2=AC2,
即x2+(2x)2=(120)2,解得x=120(舍负),
∴AD=120 米,
在Rt△ABD中,∠B=45°,∴AB=AD=240米,
240÷(120÷12)=240÷10=24(米/分钟).
答:小强以24米/分钟的速度攀登才能和小亮同时到达山顶A.
3.D 当2为等腰三角形的腰长时,三角形的三边长分别为2,2,3,能组成三角形,周长为2+2+3=3+4;
当3为等腰三角形的腰长时,三角形的三边长分别为3,3,2,能组成三角形,周长为3+3+2=6+2.综上所述,这个三角形的周长为3+4或6+2.
4.B ∵三角形的面积为12,一边长为+1,
∴该边上的高为12×2÷(+1)==24-24.
5 答案 14
解析 ∵平行四边形相邻的两边长分别是 cm和 cm,∴它的周长为2×(+)=2×(2+5)=14(cm).
能力提升全练
6.B 由题意可知∠CAD=∠CBD=60°,CD=5 m,CD⊥AB,∴△ABC是等边三角形,∴AB=AC=BC,∵CD⊥AB,∴CD是AB边上的中线,∴AD=AB.设AC=x m,则AD=x m,∴+52=x2,解得x1=,x2=-(舍去),∴拉线AC的长是 m.
7.B ∵AC=6 m,BC=3 m,
∴AB===3(m),
∵AC'=6 m,B'C'= m,
∴AB'===(m),
∴BB'=AB-AB'=3-=2(m).
8 答案 7
解析 ∵围栏的长为5米,长方形土地的宽为米,
∴长方形土地的长为5-×2=2(米),
∴该长方形土地的周长为×2+2×2=7(米).
9.答案 36
解析 该梯形的面积是×(+)×
=×(4+5)×4=×9×4=36.
10 答案 4-6
解析 ∵正方形①的边长==4,正方形③的边长=,∴正方形②的边长为4-,
∴阴影部分长方形的长=正方形③的边长=,
阴影部分长方形的宽=4--=4-2,
∴阴影部分的面积=(4-2)×=4-6.
11.答案 30
解析 设铁盒的底面边长为x cm,
可列方程为x·x·10=30×30×20,
解得x=30(舍负),
所以铁盒的底面边长为30 cm.
12.答案 566米
解析 如图,设AB与正北方向线的交点为C,在射线OC上取一点D(D在C的上方),使DC=CO,连结BD.
在Rt△ACO中,∠ACO=90°,∠AOC=45°,
∴CO=AC.设CO=AC=x米,∵CO2+AC2=OA2,
∴x2+x2=4002,解得x=200(舍负),
∴CO=AC=200米.
∵∠BCO=90°,DC=CO,∴BO=BD,
又∵∠DOB=60°,∴△OBD为等边三角形,
∴OB=OD=2CO=400≈400×1.414≈566(米).
13.解析 (1)2×(+)=2×(8+5)=(16+10)m.
答:该长方形土地的周长为(16+10)m.
(2)160×(×)=160×(8×5)=6 400≈6 400×2.449≈15 674(元).
答:在该长方形土地上全部种植草坪的总费用约为15 674元.
素养探究全练
14.解析 (1)×(3+6+7)=8,故三边长分别为3、6、7的三角形的面积为=4.
(2)如图,连结AC.
∵四边形ABCD中,AB=3,BC=4,∠B=90°,
∴AC=5,△ABC的面积=×3×4=6,
∴(AC+AD+CD)=×(5+6+7)=9,
∴△ACD的面积==6,
∴四边形ABCD的面积为6+6.
1.3 二次根式的运算
第3课时 二次根式的实际应用
基础过关全练
知识点1 坡比(坡度)问题
1.(2022贵州毕节中考)如图,某地修建的一座建筑物的截面图的高BC=5 m,坡面AB的坡度为1∶,则AB的长度为( )
A.10 m B.10 m C.5 m D.5 m
2.【一题多变·双斜坡问题求路程】(2023浙江丽水青田二中月考)如图,扶梯AB的坡比为4∶3,滑梯CD的坡比为1∶2,若AE=30 m,BC=25 m,一男孩从扶梯底走到滑梯的顶部,然后从滑梯滑下,共经过多少路程
[变式·双斜坡问题求速度]小亮和小强同时登青阳山,小亮从北坡山脚C处出发,以12 米/分钟的速度攀登,小强从南坡山脚B处出发.如图,已知青阳山北坡的坡度i=1∶2,北坡长为120米,南坡的坡角是45°.问:小强以什么速度攀登才能和小亮同时到达山顶A (将山路AB,AC看成线段)
知识点2 几何图形问题
3.【分类讨论思想】一个等腰三角形的两边长分别为2,3,则这个三角形的周长为( )
A.3+4 B.6+2
C.6+4 D.3+4或6+2
4.若一个三角形的面积为12,一边长为+1,则该边上的高为( )
A.12+12 B.24-24
C.12-12 D.24+24
5.【新独家原创】若平行四边形相邻的两边长如图所示,则它的周长为 cm.
能力提升全练
6.如图,在离地面高5 m处引拉线固定电线杆,电线杆与地面垂直,拉线与地面成60°角,则拉线AC的长是( )
A.10 m B. m C. m D.5 m
7.如图,已知鱼竿AC的长为6 m,露出水面的渔线BC的长为3 m,钓鱼者想看看鱼钩的情况,他把鱼竿AC转动到AC'的位置,此时露出水面的渔线B'C'的长为 m,则BB'的长为( )
A. m B.2 m C. m D.2 m
8.某农户用5米长的围栏和一面墙围出一块如图所示的长方形土地(墙面长恰好与长方形土地的长相等),已知该长方形土地的宽为米,则该长方形土地的周长为 米.
9.若一个梯形的上底长为,下底长为,高为,则该梯形的面积是 .
10. (2023浙江杭州临平月考,16,★★☆)如图,一个长方形被分割成四部分,其中图形①②③都是正方形,且正方形①③的面积分别为16和3,则图中阴影部分的面积为 .
11.在一个底面为正方形(边长为30 cm)的长方体玻璃容器中装满水,现将一部分水倒入一个底面为正方形,高为10 cm的铁盒中,当铁盒装满水时,长方体玻璃容器中的水面下降了20 cm,则铁盒的底面边长是 cm.
12.【国家安全】(2019浙江宁波中考,16,★★☆)如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为 .(精确到1米,参考数据:≈1.414,≈1.732)
13.在一块长方形的土地上种植草坪,该长方形土地的长为 m,宽为 m.
(1)求该长方形土地的周长;
(2)若种植草坪造价为每平方米160元,求在该长方形土地上全部种植草坪的总费用.(结果保留整数,参考数据:≈2.449)
素养探究全练
14.【运算能力】在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了利用三角形的三条边的长来求面积.我国南宋著名的数学家秦九韶提出了“三斜求积术”(利用三角形三边长求三角形面积的方法),简称为秦九韶公式.在海伦的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,故我国称这个公式为海伦-秦九韶公式.它的表述如下:三角形三边长分别为a、b、c,则三角形的面积S=(其中p为半周长,即周长的一半).
(1)求三边长分别为3、6、7的三角形的面积;
(2)四边形ABCD中,AB=3,BC=4,CD=7,AD=6,∠B=90°,求四边形ABCD的面积.
第1章 二次根式
1.3 二次根式的运算
第3课时 二次根式的实际应用
答案全解全析
基础过关全练
1.A ∵坡面AB的坡度为1∶,BC=5 m,∴=,∴AC=5 m,∴AB===10(m).
2 解析 ∵扶梯AB的坡比为4∶3,AE=30 m,
∴BE=40 m,
∴AB===50(m),
∵CF=BE=40 m,滑梯CD的坡比为1∶2,
∴FD=2CF=2×40=80(m),
∴CD===40(m),
∴经过的路程=AB+BC+CD=50+25+40=(75+40) m.
[变式]解析 如图,过点A作AD⊥BC于D.
在Rt△ACD中,i==,
设AD=x米,则CD=2x米,
根据勾股定理得AD2+CD2=AC2,
即x2+(2x)2=(120)2,解得x=120(舍负),
∴AD=120 米,
在Rt△ABD中,∠B=45°,∴AB=AD=240米,
240÷(120÷12)=240÷10=24(米/分钟).
答:小强以24米/分钟的速度攀登才能和小亮同时到达山顶A.
3.D 当2为等腰三角形的腰长时,三角形的三边长分别为2,2,3,能组成三角形,周长为2+2+3=3+4;
当3为等腰三角形的腰长时,三角形的三边长分别为3,3,2,能组成三角形,周长为3+3+2=6+2.综上所述,这个三角形的周长为3+4或6+2.
4.B ∵三角形的面积为12,一边长为+1,
∴该边上的高为12×2÷(+1)==24-24.
5 答案 14
解析 ∵平行四边形相邻的两边长分别是 cm和 cm,∴它的周长为2×(+)=2×(2+5)=14(cm).
能力提升全练
6.B 由题意可知∠CAD=∠CBD=60°,CD=5 m,CD⊥AB,∴△ABC是等边三角形,∴AB=AC=BC,∵CD⊥AB,∴CD是AB边上的中线,∴AD=AB.设AC=x m,则AD=x m,∴+52=x2,解得x1=,x2=-(舍去),∴拉线AC的长是 m.
7.B ∵AC=6 m,BC=3 m,
∴AB===3(m),
∵AC'=6 m,B'C'= m,
∴AB'===(m),
∴BB'=AB-AB'=3-=2(m).
8 答案 7
解析 ∵围栏的长为5米,长方形土地的宽为米,
∴长方形土地的长为5-×2=2(米),
∴该长方形土地的周长为×2+2×2=7(米).
9.答案 36
解析 该梯形的面积是×(+)×
=×(4+5)×4=×9×4=36.
10 答案 4-6
解析 ∵正方形①的边长==4,正方形③的边长=,∴正方形②的边长为4-,
∴阴影部分长方形的长=正方形③的边长=,
阴影部分长方形的宽=4--=4-2,
∴阴影部分的面积=(4-2)×=4-6.
11.答案 30
解析 设铁盒的底面边长为x cm,
可列方程为x·x·10=30×30×20,
解得x=30(舍负),
所以铁盒的底面边长为30 cm.
12.答案 566米
解析 如图,设AB与正北方向线的交点为C,在射线OC上取一点D(D在C的上方),使DC=CO,连结BD.
在Rt△ACO中,∠ACO=90°,∠AOC=45°,
∴CO=AC.设CO=AC=x米,∵CO2+AC2=OA2,
∴x2+x2=4002,解得x=200(舍负),
∴CO=AC=200米.
∵∠BCO=90°,DC=CO,∴BO=BD,
又∵∠DOB=60°,∴△OBD为等边三角形,
∴OB=OD=2CO=400≈400×1.414≈566(米).
13.解析 (1)2×(+)=2×(8+5)=(16+10)m.
答:该长方形土地的周长为(16+10)m.
(2)160×(×)=160×(8×5)=6 400≈6 400×2.449≈15 674(元).
答:在该长方形土地上全部种植草坪的总费用约为15 674元.
素养探究全练
14.解析 (1)×(3+6+7)=8,故三边长分别为3、6、7的三角形的面积为=4.
(2)如图,连结AC.
∵四边形ABCD中,AB=3,BC=4,∠B=90°,
∴AC=5,△ABC的面积=×3×4=6,
∴(AC+AD+CD)=×(5+6+7)=9,
∴△ACD的面积==6,
∴四边形ABCD的面积为6+6.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
