浙教版数学八年级下册3.3 方差和标准差 素养提升练习(含解析)
文档属性
| 名称 | 浙教版数学八年级下册3.3 方差和标准差 素养提升练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 161.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 18:50:21 | ||
图片预览



文档简介
第3章 数据分析初步
3.3 方差和标准差
基础过关全练
知识点1 方差
1.要从甲、乙、丙三人中选拔一人参加职业技能大赛,经过几轮初赛选拔,他们的平均成绩都是88分,甲的方差为3.83,乙的方差为2.71,丙的方差为1.52,若选取成绩稳定的一人参加比赛,你认为适合参加比赛的选手是( )
A.甲 B.乙 C.丙 D.无法判断
2.(2023浙江衢州柯城风华学校期中)已知一组数据的方差计算公式是S2=[(8-)2+(8-)2+(9-)2+(11-)2] ,下列关于这组数据的说法错误的是( )
A.平均数是9 B.中位数是8.5 C.方差是2 D.众数是8
3.【生命安全与健康】【新课标例85变式】某校在评选“交通安全在我心”优秀宣传小队的活动中,分别对甲、乙两队的5名学生进行了交通安全知识考核,其中甲、乙两队学生的考核成绩如图所示,下列关系完全正确的是( )
A.<,= B.>,=
C.=,< D.=,>
4.【教材变式·P62合作学习】【浙江名人·徐志摩】徐志摩的《泰山日出》一文描写了“泰山佛光”的壮丽景象.某月1日至5日泰山山脚的最低气温分别为-1℃,-1℃,-2℃,0℃,-1℃,则这五天最低气温的方差是 .
知识点2 标准差
5.【新独家原创】小林五天来在某平台收到的关注人数如下表所示:
第1天 第2天 第3天 第4天 第5天
1 3 4 5 1
则这五天关注人数的标准差是( )
A.2.56 B.0 C.1.6 D.0.8
6.(2023浙江湖州长兴一模)已知一组数据的方差为2,则这组数据的标准差为 .
7.已知某排球队6名场上队员的身高(单位:cm)分别是181,185,188,190,194,196.现用两名身高分别是186,195的队员换下场上身高为181,194的队员,与换人前相比,标准差 (填“变小”“变大”或“不变”).
8.已知一组数据:4、0、2、1、-2,分别计算这组数据的平均数、方差和标准差.
能力提升全练
9.【跨学科·体育与健康】(2023山东滨州中考,6,★★☆)在某次射击训练过程中,小明打靶10次的成绩(单位:环)如表所示,则小明射击成绩的众数和方差分别为( )
靶次 第 1 次 第 2 次 第 3 次 第 4 次 第 5 次 第 6 次 第 7 次 第 8 次 第 9 次 第 10 次
成绩 (环) 8 9 9 10 10 7 8 9 10 10
A.10环和0.1 B.9环和0.1 C.10环和1 D.9环和1
10.(2022浙江宁波慈溪期末,6,★★☆)有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
11.【跨学科·体育与健康】(2023浙江杭州上城一模,7,★★☆)跳远运动员小李在一次训练中,跳了6次的成绩(单位:m)如下:7.6,7.8,7.7,7.8,8.0,7.9,这六次成绩的平均数为7.8,方差为.如果小李再跳一次,成绩为7.8(单位:m),则小李这7次跳远成绩与前6次的成绩相比较,其方差( )
A.变大 B.变小 C.不变 D.无法确定
12.(2023浙江温岭一模,8,★★☆)顶呱呱学习小组5名同学某次数学成绩如图所示,拿到试卷后,小刚发现自己的成绩少加了10分,老师加回分数后,下列说法正确的是( )
A.小刚加分后的成绩位于组内中等水平
B.小组平均分增加2分
C.小组的成绩稳定性增加,方差变大
D.该小组成绩不存在中位数
13.(2023浙江杭州外国语学校期中,13,★★☆)数据3、1、x、-1、-3的平均数是0,则这组数据的方差是 .
14.(2023山东淄博张店期末,19,★★☆)小聪、小明准备代表班级参加学校“党史知识”竞赛,班主任对这两名同学进行了6次测试,测试成绩折线统计图如图所示.
根据图中信息,解答下列问题:
(1)要评价两名同学成绩的平均水平,你选择什么统计量 求这个统计量.
(2)求小聪成绩的方差.
(3)现求得小明成绩的方差为3,根据折线统计图及上面两小题的计算,你认为哪名同学的成绩较好 请简述理由.
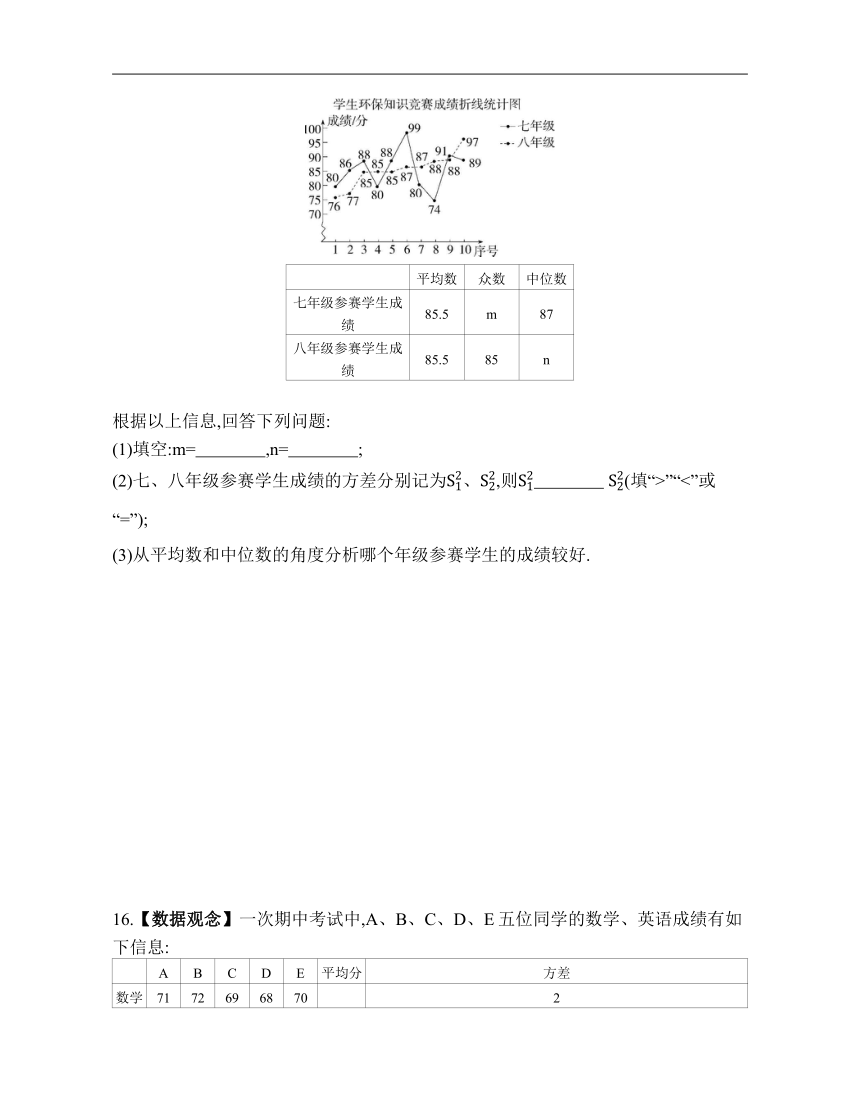
15.【数据观念】(2023江苏扬州中考)某校为了普及环保知识,从七、八两个年级中各选出10名学生参加环保知识竞赛(满分100分),并对成绩进行整理分析,得到如下信息:
平均数 众数 中位数
七年级参赛学生成绩 85.5 m 87
八年级参赛学生成绩 85.5 85 n
根据以上信息,回答下列问题:
(1)填空:m= ,n= ;
(2)七、八年级参赛学生成绩的方差分别记为、,则 (填“>”“<”或“=”);
(3)从平均数和中位数的角度分析哪个年级参赛学生的成绩较好.
16.【数据观念】一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
A B C D E 平均分 方差
数学 71 72 69 68 70 2
英语 88 82 94 85 76 85
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是标准分=,
从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好 (说明:标准差为方差的算术平方根)
第3章 数据分析初步
3.3 方差和标准差
答案全解全析
基础过关全练
1.C ∵平均成绩都是88分,甲的方差为3.83,乙的方差为2.71,丙的方差为1.52,
∴S丙22.C 由S2=[(8-)2+(8-)2+(9-)2+(11-)2]可知,这组数据为8,8,9,11,所以这组数据的平均数是=9,所以A正确;
这组数据的中位数是=8.5,所以B正确;
这组数据的方差是S2=[(8-9)2+(8-9)2+(9-9)2+(11-9)2]=1.5,所以C错误;
8出现2次,9出现1次,11出现1次,8出现的次数最多,所以众数是8,所以D正确.故选C.
3.A =×(60+70+70+60+80)=68(分),=×(70+80+80+70+90)=78(分),∴<,
由折线统计图可得=,故选A.
4 答案 0.4
解析 这五天最低气温的平均值是(-1-1-2+0-1)=-1(℃),这五天最低气温的方差是
[(-1+1)2+(-1+1)2+(-2+1)2+(0+1)2+(-1+1)2]=0.4.
5.C 这五天关注人数的平均值为(1+3+4+5+1)=2.8,所以这五天关注人数的标准差是=1.6.
6 答案
解析 根据“一组数据的方差的算术平方根称为这组数据的标准差”,可得这组数据的标准差为.
7 答案 变小
解析 原来的平均数为(181+185+188+190+194+196)÷6=189,
替换的后平均数为(186+185+188+190+195+196)÷6=190,
原来的方差为[(181-189)2+(185-189)2+(188-189)2+(190-189)2+(194-189)2+(196-189)2]÷6=26,
替换后的方差为[(186-190)2+(185-190)2+(188-190)2+(190-190)2+(195-190)2+(196-190)2]÷6≈17.7,
方差变小,所以标准差也变小.
8.解析 这组数据的平均数是×(4+0+2+1-2)=1;这组数据的方差是×[(4-1)2+(0-1)2+(2-1)2+(1-1)2+(-2-1)2]=4,∴这组数据的标准差是=2.
能力提升全练
9.C 由题意可知,10环出现的次数最多,为4次,故众数为10环;
这10次成绩的平均数为×(7+2×8+3×9+4×10)=9环,
故这10次成绩的方差为×[(7-9)2+2×(8-9)2+3×(9-9)2+4×(10-9)2]=1.
故选C.
10.B 根据中位数的定义可知一组数据去掉一个最高分和一个最低分不影响中位数.
11.B ∵小李再跳1次,成绩为7.8 m,
∴这组数据的平均数是=7.8(m),
∴这7次跳远成绩的方差是[(7.6-7.8)2+3×(7.8-7.8)2+(7.7-7.8)2+(8.0-7.8)2+(7.9-7.8)2]=,∵<,∴方差变小.故选B.
12.B 从题图中可以得出小刚加分前的成绩小于70分,B同学成绩大于80分而小于90分,A同学成绩大于B同学成绩而小于90分,D同学成绩大于90分而小于100分,E同学成绩为90分.小刚的成绩加上10分后,仍然处于下等水平,所以A说法错误;小刚的成绩加上10分后,小组的平均分增加=2分,所以B说法正确;小组的成绩稳定性增加,方差变小,所以C说法错误;该小组成绩存在中位数为A的成绩,所以D说法错误.故选B.
13 答案 4
解析 ∵数据3、1、x、-1、-3的平均数为0,
∴(3+1+x-1-3)=0,解得x=0,
∴这组数据的方差是[(3-0)2+(1-0)2+(0-0)2+(-1-0)2+(-3-0)2]=4.故填4.
14.解析 (1)要评价两名同学成绩的平均水平,选择平均数即可,
小聪成绩的平均数=×(7+8+7+10+7+9)=8(分),
小明成绩的平均数=×(7+6+6+9+10+10)=8(分).
(2)小聪成绩的方差为×[(7-8)2+(8-8)2+(7-8)2+(10-8)2+(7-8)2+(9-8)2]=.
(3)小聪的成绩较好.
理由:由(1)可知两人成绩的平均数相同,因为小聪成绩的方差小于小明成绩的方差,所以小聪成绩相对稳定.故小聪的成绩较好.
素养探究全练
15 解析 (1)七年级成绩中80分的最多,有3个,所以m=80,
将八年级成绩从小到大排列为76,77,85,85,85,87,87,88,88,97,处于中间位置的两个数据为85和87,
所以n==86.
故答案为80;86.
(2)=×[(74-85.5)2+3×(80-85.5)2+(86-85.5)2+2×(88-85.5)2+(89-85.5)2+(91-85.5)2+(99-85.5)2]=46.05,
=×[(76-85.5)2+(77-85.5)2+3×(85-85.5)2+2×(87-85.5)2+2×(88-85.5)2+(97-85.5)2]=31.25,
∴>.故答案为>.
(3)因为平均数相同,七年级参赛学生成绩的中位数较大,所以七年级参赛学生的成绩较好.
16.解析 (1)数学成绩的平均分为=70,
英语成绩的方差为×[(88-85)2+(82-85)2+(94-85)2+(85-85)2+(76-85)2]=36.
(2)A同学数学标准分为=,
A同学英语标准分为=,
因为>,所以A同学在本次考试中,数学学科考得更好.
3.3 方差和标准差
基础过关全练
知识点1 方差
1.要从甲、乙、丙三人中选拔一人参加职业技能大赛,经过几轮初赛选拔,他们的平均成绩都是88分,甲的方差为3.83,乙的方差为2.71,丙的方差为1.52,若选取成绩稳定的一人参加比赛,你认为适合参加比赛的选手是( )
A.甲 B.乙 C.丙 D.无法判断
2.(2023浙江衢州柯城风华学校期中)已知一组数据的方差计算公式是S2=[(8-)2+(8-)2+(9-)2+(11-)2] ,下列关于这组数据的说法错误的是( )
A.平均数是9 B.中位数是8.5 C.方差是2 D.众数是8
3.【生命安全与健康】【新课标例85变式】某校在评选“交通安全在我心”优秀宣传小队的活动中,分别对甲、乙两队的5名学生进行了交通安全知识考核,其中甲、乙两队学生的考核成绩如图所示,下列关系完全正确的是( )
A.<,= B.>,=
C.=,< D.=,>
4.【教材变式·P62合作学习】【浙江名人·徐志摩】徐志摩的《泰山日出》一文描写了“泰山佛光”的壮丽景象.某月1日至5日泰山山脚的最低气温分别为-1℃,-1℃,-2℃,0℃,-1℃,则这五天最低气温的方差是 .
知识点2 标准差
5.【新独家原创】小林五天来在某平台收到的关注人数如下表所示:
第1天 第2天 第3天 第4天 第5天
1 3 4 5 1
则这五天关注人数的标准差是( )
A.2.56 B.0 C.1.6 D.0.8
6.(2023浙江湖州长兴一模)已知一组数据的方差为2,则这组数据的标准差为 .
7.已知某排球队6名场上队员的身高(单位:cm)分别是181,185,188,190,194,196.现用两名身高分别是186,195的队员换下场上身高为181,194的队员,与换人前相比,标准差 (填“变小”“变大”或“不变”).
8.已知一组数据:4、0、2、1、-2,分别计算这组数据的平均数、方差和标准差.
能力提升全练
9.【跨学科·体育与健康】(2023山东滨州中考,6,★★☆)在某次射击训练过程中,小明打靶10次的成绩(单位:环)如表所示,则小明射击成绩的众数和方差分别为( )
靶次 第 1 次 第 2 次 第 3 次 第 4 次 第 5 次 第 6 次 第 7 次 第 8 次 第 9 次 第 10 次
成绩 (环) 8 9 9 10 10 7 8 9 10 10
A.10环和0.1 B.9环和0.1 C.10环和1 D.9环和1
10.(2022浙江宁波慈溪期末,6,★★☆)有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
11.【跨学科·体育与健康】(2023浙江杭州上城一模,7,★★☆)跳远运动员小李在一次训练中,跳了6次的成绩(单位:m)如下:7.6,7.8,7.7,7.8,8.0,7.9,这六次成绩的平均数为7.8,方差为.如果小李再跳一次,成绩为7.8(单位:m),则小李这7次跳远成绩与前6次的成绩相比较,其方差( )
A.变大 B.变小 C.不变 D.无法确定
12.(2023浙江温岭一模,8,★★☆)顶呱呱学习小组5名同学某次数学成绩如图所示,拿到试卷后,小刚发现自己的成绩少加了10分,老师加回分数后,下列说法正确的是( )
A.小刚加分后的成绩位于组内中等水平
B.小组平均分增加2分
C.小组的成绩稳定性增加,方差变大
D.该小组成绩不存在中位数
13.(2023浙江杭州外国语学校期中,13,★★☆)数据3、1、x、-1、-3的平均数是0,则这组数据的方差是 .
14.(2023山东淄博张店期末,19,★★☆)小聪、小明准备代表班级参加学校“党史知识”竞赛,班主任对这两名同学进行了6次测试,测试成绩折线统计图如图所示.
根据图中信息,解答下列问题:
(1)要评价两名同学成绩的平均水平,你选择什么统计量 求这个统计量.
(2)求小聪成绩的方差.
(3)现求得小明成绩的方差为3,根据折线统计图及上面两小题的计算,你认为哪名同学的成绩较好 请简述理由.
15.【数据观念】(2023江苏扬州中考)某校为了普及环保知识,从七、八两个年级中各选出10名学生参加环保知识竞赛(满分100分),并对成绩进行整理分析,得到如下信息:
平均数 众数 中位数
七年级参赛学生成绩 85.5 m 87
八年级参赛学生成绩 85.5 85 n
根据以上信息,回答下列问题:
(1)填空:m= ,n= ;
(2)七、八年级参赛学生成绩的方差分别记为、,则 (填“>”“<”或“=”);
(3)从平均数和中位数的角度分析哪个年级参赛学生的成绩较好.
16.【数据观念】一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
A B C D E 平均分 方差
数学 71 72 69 68 70 2
英语 88 82 94 85 76 85
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是标准分=,
从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好 (说明:标准差为方差的算术平方根)
第3章 数据分析初步
3.3 方差和标准差
答案全解全析
基础过关全练
1.C ∵平均成绩都是88分,甲的方差为3.83,乙的方差为2.71,丙的方差为1.52,
∴S丙2
这组数据的中位数是=8.5,所以B正确;
这组数据的方差是S2=[(8-9)2+(8-9)2+(9-9)2+(11-9)2]=1.5,所以C错误;
8出现2次,9出现1次,11出现1次,8出现的次数最多,所以众数是8,所以D正确.故选C.
3.A =×(60+70+70+60+80)=68(分),=×(70+80+80+70+90)=78(分),∴<,
由折线统计图可得=,故选A.
4 答案 0.4
解析 这五天最低气温的平均值是(-1-1-2+0-1)=-1(℃),这五天最低气温的方差是
[(-1+1)2+(-1+1)2+(-2+1)2+(0+1)2+(-1+1)2]=0.4.
5.C 这五天关注人数的平均值为(1+3+4+5+1)=2.8,所以这五天关注人数的标准差是=1.6.
6 答案
解析 根据“一组数据的方差的算术平方根称为这组数据的标准差”,可得这组数据的标准差为.
7 答案 变小
解析 原来的平均数为(181+185+188+190+194+196)÷6=189,
替换的后平均数为(186+185+188+190+195+196)÷6=190,
原来的方差为[(181-189)2+(185-189)2+(188-189)2+(190-189)2+(194-189)2+(196-189)2]÷6=26,
替换后的方差为[(186-190)2+(185-190)2+(188-190)2+(190-190)2+(195-190)2+(196-190)2]÷6≈17.7,
方差变小,所以标准差也变小.
8.解析 这组数据的平均数是×(4+0+2+1-2)=1;这组数据的方差是×[(4-1)2+(0-1)2+(2-1)2+(1-1)2+(-2-1)2]=4,∴这组数据的标准差是=2.
能力提升全练
9.C 由题意可知,10环出现的次数最多,为4次,故众数为10环;
这10次成绩的平均数为×(7+2×8+3×9+4×10)=9环,
故这10次成绩的方差为×[(7-9)2+2×(8-9)2+3×(9-9)2+4×(10-9)2]=1.
故选C.
10.B 根据中位数的定义可知一组数据去掉一个最高分和一个最低分不影响中位数.
11.B ∵小李再跳1次,成绩为7.8 m,
∴这组数据的平均数是=7.8(m),
∴这7次跳远成绩的方差是[(7.6-7.8)2+3×(7.8-7.8)2+(7.7-7.8)2+(8.0-7.8)2+(7.9-7.8)2]=,∵<,∴方差变小.故选B.
12.B 从题图中可以得出小刚加分前的成绩小于70分,B同学成绩大于80分而小于90分,A同学成绩大于B同学成绩而小于90分,D同学成绩大于90分而小于100分,E同学成绩为90分.小刚的成绩加上10分后,仍然处于下等水平,所以A说法错误;小刚的成绩加上10分后,小组的平均分增加=2分,所以B说法正确;小组的成绩稳定性增加,方差变小,所以C说法错误;该小组成绩存在中位数为A的成绩,所以D说法错误.故选B.
13 答案 4
解析 ∵数据3、1、x、-1、-3的平均数为0,
∴(3+1+x-1-3)=0,解得x=0,
∴这组数据的方差是[(3-0)2+(1-0)2+(0-0)2+(-1-0)2+(-3-0)2]=4.故填4.
14.解析 (1)要评价两名同学成绩的平均水平,选择平均数即可,
小聪成绩的平均数=×(7+8+7+10+7+9)=8(分),
小明成绩的平均数=×(7+6+6+9+10+10)=8(分).
(2)小聪成绩的方差为×[(7-8)2+(8-8)2+(7-8)2+(10-8)2+(7-8)2+(9-8)2]=.
(3)小聪的成绩较好.
理由:由(1)可知两人成绩的平均数相同,因为小聪成绩的方差小于小明成绩的方差,所以小聪成绩相对稳定.故小聪的成绩较好.
素养探究全练
15 解析 (1)七年级成绩中80分的最多,有3个,所以m=80,
将八年级成绩从小到大排列为76,77,85,85,85,87,87,88,88,97,处于中间位置的两个数据为85和87,
所以n==86.
故答案为80;86.
(2)=×[(74-85.5)2+3×(80-85.5)2+(86-85.5)2+2×(88-85.5)2+(89-85.5)2+(91-85.5)2+(99-85.5)2]=46.05,
=×[(76-85.5)2+(77-85.5)2+3×(85-85.5)2+2×(87-85.5)2+2×(88-85.5)2+(97-85.5)2]=31.25,
∴>.故答案为>.
(3)因为平均数相同,七年级参赛学生成绩的中位数较大,所以七年级参赛学生的成绩较好.
16.解析 (1)数学成绩的平均分为=70,
英语成绩的方差为×[(88-85)2+(82-85)2+(94-85)2+(85-85)2+(76-85)2]=36.
(2)A同学数学标准分为=,
A同学英语标准分为=,
因为>,所以A同学在本次考试中,数学学科考得更好.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
