2.8 直角三角形全等的判定同步练习(无答案)2023-2024学年浙教版八年级数学上册
文档属性
| 名称 | 2.8 直角三角形全等的判定同步练习(无答案)2023-2024学年浙教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 319.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-24 19:22:52 | ||
图片预览


文档简介
浙教版八年级上册2.8 直角三角形全等的判定
一、选择题
1. 下列条件,不能判定两个直角三角形全等的是( )
A.两个锐角对应相等 B.斜边和一直角边分别对应相等
C.两条直角边分别对应相等 D.一条直角边相等且另一条直角边上的中线对应相等
2. 在RtΔABC中,∠ACB=90°,E是AB上一点,且BE=BC,过E作DE⊥AB交AC于D,如果AC=5cm,则AD+DE=( )
A.3 B.5 C.7 D.9
3. 小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
4. 如图,AB⊥BC于点B,AD⊥DC于点D,若CB=CD,且∠1=30°,则∠BAD的度数是( )
A.90° B.60° C.30° D.15°
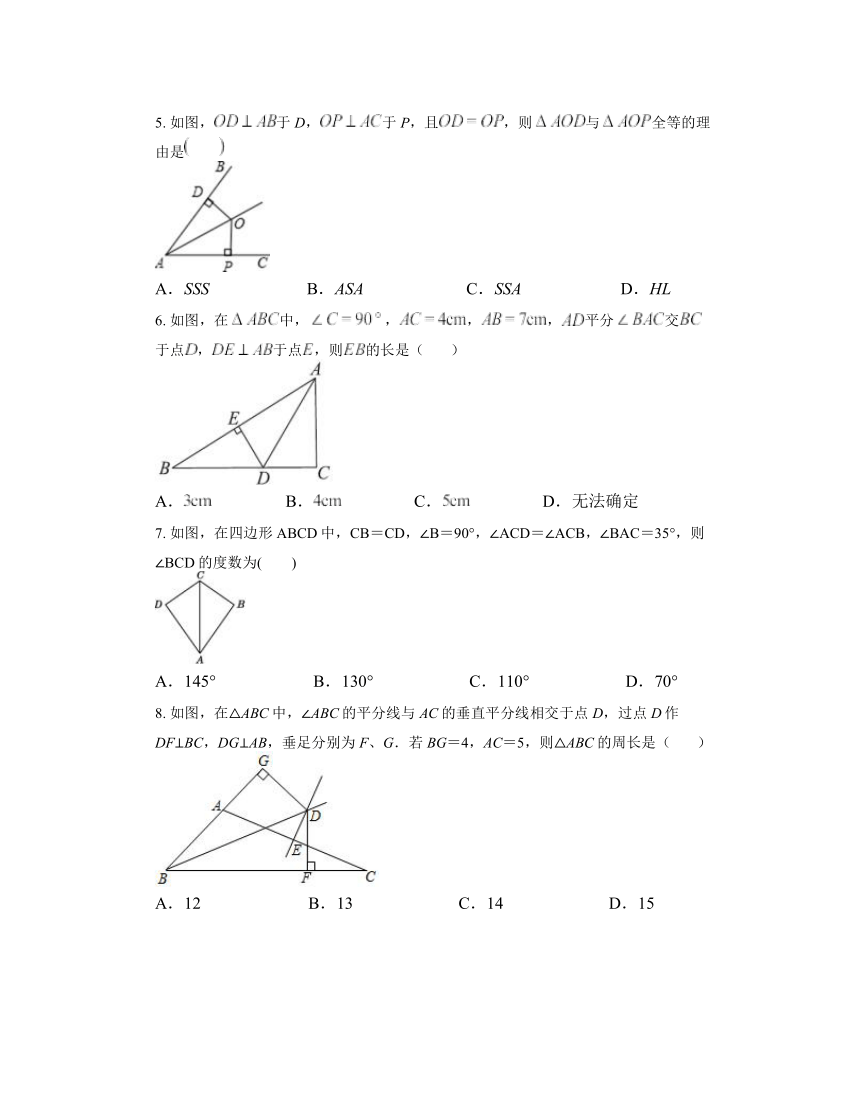
5. 如图,于D,于P,且,则与全等的理由是
A.SSS B.ASA C.SSA D.HL
6. 如图,在中,,,,平分交于点,于点,则的长是( )
A. B. C. D.无法确定
7. 如图,在四边形ABCD中,CB=CD,∠B=90°,∠ACD=∠ACB,∠BAC=35°,则∠BCD的度数为( )
A.145° B.130° C.110° D.70°
8. 如图,在△ABC中,∠ABC的平分线与AC的垂直平分线相交于点D,过点D作DF⊥BC,DG⊥AB,垂足分别为F、G.若BG=4,AC=5,则△ABC的周长是( )
A.12 B.13 C.14 D.15
9. 如图是的角平分线,于,点,分别是,上的点,且,与的面积分别是10和3,则的面积是( )
A.4 B.5 C.6 D.7
10. 如图,在的两边上分别取点,使得,将两个全等的直角三角板的直角顶点分别放在点,处,一条直角边分别落在的两边上,另一条直角边交于点,连接,则判定的依据是( )
A. B. C. D.
11. 如图,Rt中,,,是的平分线,于,,,则的长为( )
A. B. C. D.
12. “勾股图”有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了以“勾股图”为背景的邮票(如图1),欧几里得在《几何原本》中曾对该图做了深入研究.如图2,在中,,分别以的三条边为边向外作正方形,连结,,,分别与,相交于点,.若,则的值为( )
A. B. C. D.
二、填空题
13. 阅读下面材料:
在数学课上,老师提出如下问题:
小芸的作图步骤如下:
老师说:“小芸的作图步骤正确,且可以得到DF=AC”.
请回答:得到DF=AC的依据是_________________________.
14. 如图中,平分于,给出下列结论:①;②平分;③平分;④;⑤.其中正确的是______________.(写序号)
15. 如图,在中,,以A为圆心、适当长为半径画弧,分别交、于点M、N,再分别以M、N为圆心,大于长为半径画弧,两弧交于点D,作射线,交于点E.已知,若P为上一点,当时,线段的长为___________.
16. 甲乙两位同学进行一种数学游戏,游戏规则是:两人轮流对及对应的边或角添加等量条件(点,,分别是点A,B,C的对应点).某轮添加条件后,若能判定与全等,则当轮添加条件者失败,另一人获胜.
轮次 行动者 添加条件
1 甲
2 乙
3 甲 …
①若第3轮甲添加,则乙获胜;
②若甲想获胜,第3轮可以添加条件;
③若乙想获胜,可修改第2轮添加条件为.
上表记录了两人游戏的部分过程,则下列说法正确的是______(填写所有正确结论的序号).
三、解答题
17. 如图,已知,,与交于O,.
求证:
(1);
(2)点O在线段的垂直平分线上.
18. 已知:如图,在和中,,,垂足分别为,,,求证:是等腰三角形.
19. 如图,是的角平分线,,分别是和的高.
求证:
(1);
(2)垂直平分.
20. 如图,为直角三角形,,点D在上,连接.
(1)在边上作点E,使得点E到的距离与长相等;(要求:仅用圆规作图,不写作法,保留作图痕迹)(保留作图痕迹)
(2)在(1)的条件下继续探究,若,,,求CD的长.
一、选择题
1. 下列条件,不能判定两个直角三角形全等的是( )
A.两个锐角对应相等 B.斜边和一直角边分别对应相等
C.两条直角边分别对应相等 D.一条直角边相等且另一条直角边上的中线对应相等
2. 在RtΔABC中,∠ACB=90°,E是AB上一点,且BE=BC,过E作DE⊥AB交AC于D,如果AC=5cm,则AD+DE=( )
A.3 B.5 C.7 D.9
3. 小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
A.SSS B.SAS C.ASA D.HL
4. 如图,AB⊥BC于点B,AD⊥DC于点D,若CB=CD,且∠1=30°,则∠BAD的度数是( )
A.90° B.60° C.30° D.15°
5. 如图,于D,于P,且,则与全等的理由是
A.SSS B.ASA C.SSA D.HL
6. 如图,在中,,,,平分交于点,于点,则的长是( )
A. B. C. D.无法确定
7. 如图,在四边形ABCD中,CB=CD,∠B=90°,∠ACD=∠ACB,∠BAC=35°,则∠BCD的度数为( )
A.145° B.130° C.110° D.70°
8. 如图,在△ABC中,∠ABC的平分线与AC的垂直平分线相交于点D,过点D作DF⊥BC,DG⊥AB,垂足分别为F、G.若BG=4,AC=5,则△ABC的周长是( )
A.12 B.13 C.14 D.15
9. 如图是的角平分线,于,点,分别是,上的点,且,与的面积分别是10和3,则的面积是( )
A.4 B.5 C.6 D.7
10. 如图,在的两边上分别取点,使得,将两个全等的直角三角板的直角顶点分别放在点,处,一条直角边分别落在的两边上,另一条直角边交于点,连接,则判定的依据是( )
A. B. C. D.
11. 如图,Rt中,,,是的平分线,于,,,则的长为( )
A. B. C. D.
12. “勾股图”有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了以“勾股图”为背景的邮票(如图1),欧几里得在《几何原本》中曾对该图做了深入研究.如图2,在中,,分别以的三条边为边向外作正方形,连结,,,分别与,相交于点,.若,则的值为( )
A. B. C. D.
二、填空题
13. 阅读下面材料:
在数学课上,老师提出如下问题:
小芸的作图步骤如下:
老师说:“小芸的作图步骤正确,且可以得到DF=AC”.
请回答:得到DF=AC的依据是_________________________.
14. 如图中,平分于,给出下列结论:①;②平分;③平分;④;⑤.其中正确的是______________.(写序号)
15. 如图,在中,,以A为圆心、适当长为半径画弧,分别交、于点M、N,再分别以M、N为圆心,大于长为半径画弧,两弧交于点D,作射线,交于点E.已知,若P为上一点,当时,线段的长为___________.
16. 甲乙两位同学进行一种数学游戏,游戏规则是:两人轮流对及对应的边或角添加等量条件(点,,分别是点A,B,C的对应点).某轮添加条件后,若能判定与全等,则当轮添加条件者失败,另一人获胜.
轮次 行动者 添加条件
1 甲
2 乙
3 甲 …
①若第3轮甲添加,则乙获胜;
②若甲想获胜,第3轮可以添加条件;
③若乙想获胜,可修改第2轮添加条件为.
上表记录了两人游戏的部分过程,则下列说法正确的是______(填写所有正确结论的序号).
三、解答题
17. 如图,已知,,与交于O,.
求证:
(1);
(2)点O在线段的垂直平分线上.
18. 已知:如图,在和中,,,垂足分别为,,,求证:是等腰三角形.
19. 如图,是的角平分线,,分别是和的高.
求证:
(1);
(2)垂直平分.
20. 如图,为直角三角形,,点D在上,连接.
(1)在边上作点E,使得点E到的距离与长相等;(要求:仅用圆规作图,不写作法,保留作图痕迹)(保留作图痕迹)
(2)在(1)的条件下继续探究,若,,,求CD的长.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
