一次函数复习课

课件56张PPT。一次函数复习 生活中充满着许许多多变化着的量与不变的量,它们之间还常常存在着一定的关系.函数是刻画变量之间的关系的一个数学模型. 函数的定义：
一般地，在某一变化过程中，有两个变量x和y,并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数．当x=a时，y＝b,那么b叫做当自变量的值为a 时的函数值．函数的表示方法:
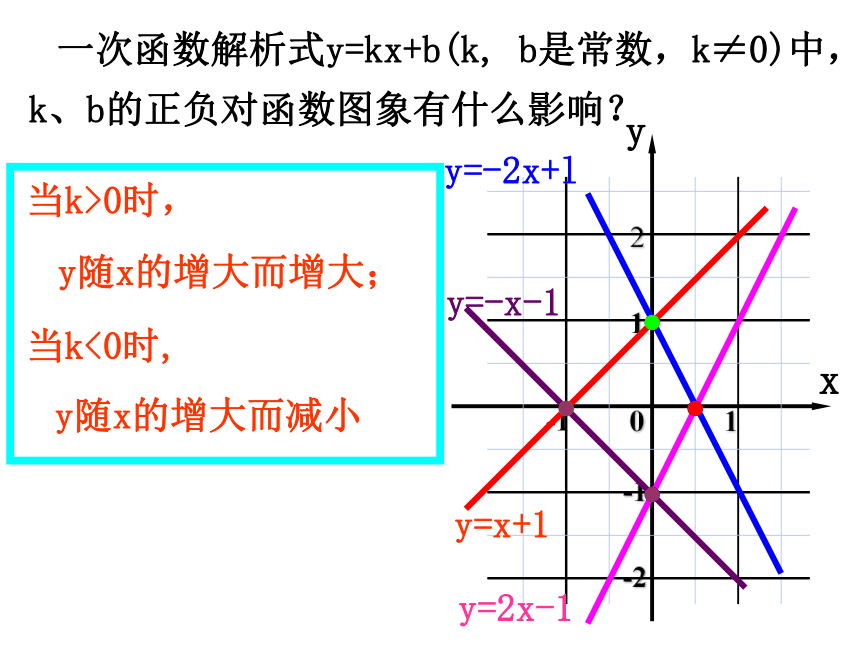
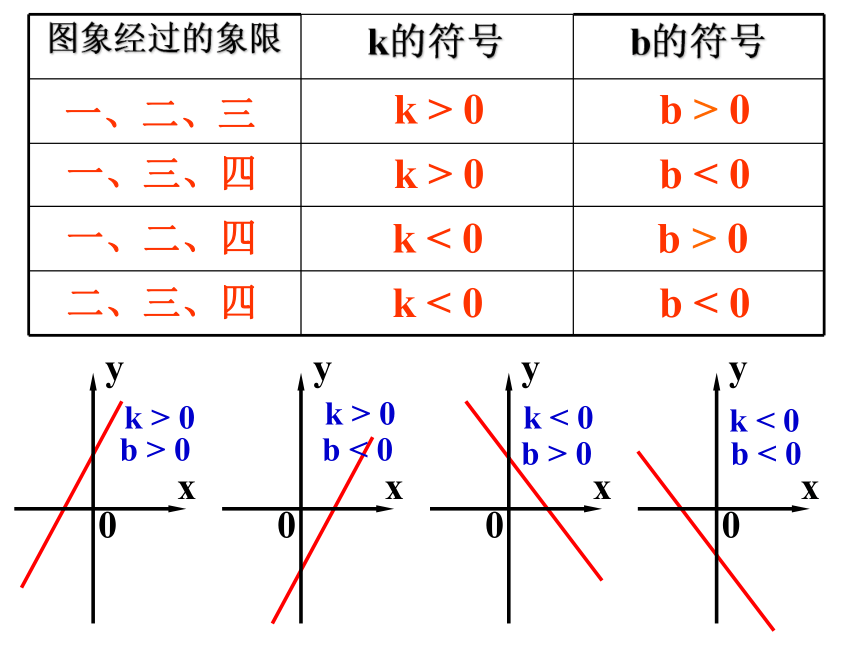
(1)列表法 (2)解析式法 (3)图象法。 特别地,当b=0时,称y是x的正比例函数.什么叫一次函数? 若两个变量x,y间的关系式可以表示成y=kx+b (k,b为常数,k不为零）的形式,则称y是x的一次函数 . 其中x为自变量. 一次函数解析式y=kx+b(k, b是常数，k≠0)中，k、b的正负对函数图象有什么影响？当k>0时，当k<0时, y随x的增大而增大；y随x的增大而减小 k > 0 k < 0一、二、三一、三、四一、二、四二、三、四 k > 0 k < 0 b < 0 b < 0 b > 0 b > 0 k > 0 k > 0 k < 0 k < 0 b < 0 b < 0 b > 0 b > 0求下列函数中自变量的取值范围:(1)y=3x-6 (2)y=
(4)y=(3X+2)0 (3)y= (6)(5) 1、下列函数中, y=-8x , y=-8x+1, y=8x2+1, y=-8/x,是一次函数的有( )个.
A. 1 B. 2 C. 3 D. 4BB3、填空题：
(1)　有下列函数：①　　　　 ,② y=2x,
③　　　 ,④ 。其中过原点的直
线是_____；函数y随x的增大而增大的是___________；函数y随x的增大而减小的是______；图象在第一、二、三象限的是_____。②①、②、③④③ (2)已知y-1与x成正比例，且x=－2时，y=4，那么y与
x之间的函数关系式为_________________。4、将直线y＝2x向右平移2个单位所得的直线的解析式是（ ）
A、y＝2x＋2 B、y＝2x－2
C、y＝2(x－2) D、y＝2(x＋2)5、如果函数y=ax+b(a<0，b<0)和y=kx(k>0)的图象交于点P，那么点P应该位于( )
(A)第一象限 (B)第二象限
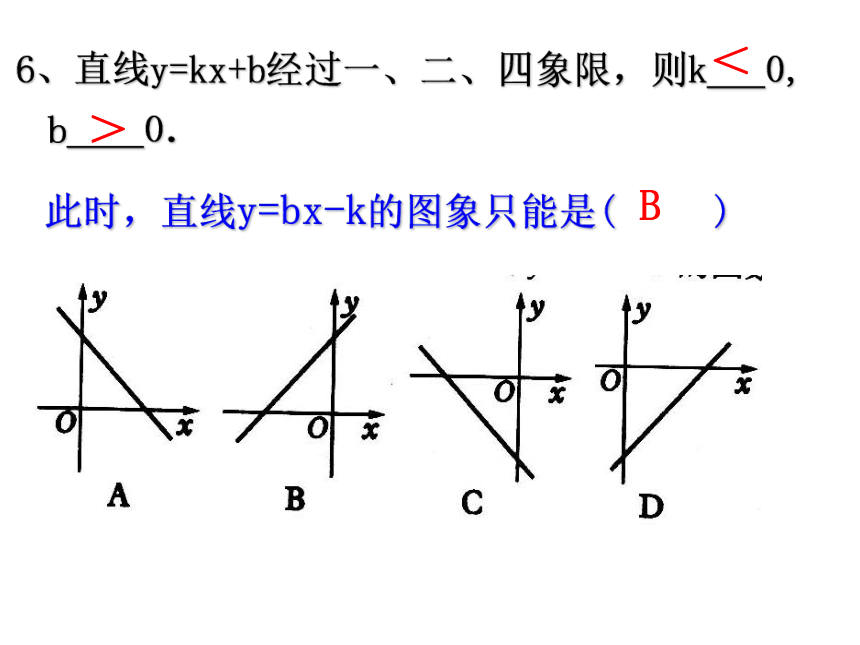
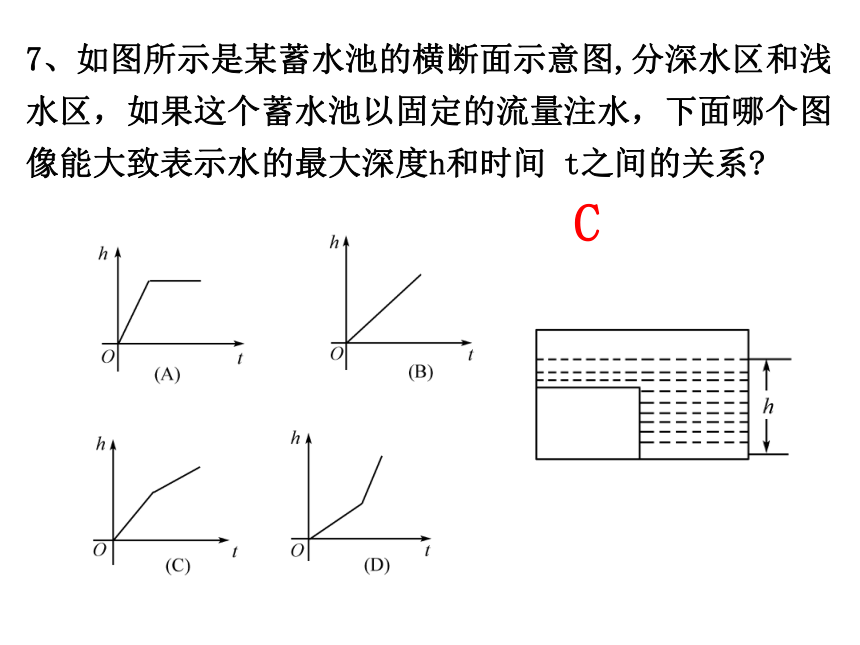
(C)第三象限 (D)第四象限CC6、直线y=kx+b经过一、二、四象限，则k 0, b 0．＜＞此时，直线y=bx-k的图象只能是( ) BC7、如图所示是某蓄水池的横断面示意图,分深水区和浅水区，如果这个蓄水池以固定的流量注水，下面哪个图像能大致表示水的最大深度h和时间 t之间的关系?B8、如图,向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度h与注水时间t之间的函数关系，大致是下列图像中的 ( )A10、如图,小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快了骑车速度继续匀速行驶,下面是行驶路程s(米)关于时间t(分)的函数图像,那么符合小明行驶情况的图像大致是 ( )C11、星期天晚饭后,小红从家里出去散步,如下图所示描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系,依据图像,下面描述符合小红散步情景的是 ( )
A.从家出发,到一个公共阅报栏,看了一会儿报,就回家了.
B.从家出发,到了一个公共阅报栏,
看了一会儿报后,继续向前走了一
段,然后回家了.
C.从家出发,一直散步(没有停留),
然后回家了.
D.从家出发,散了一会儿步,就找同
学去了,18分钟后才开始返回.B(1)k为何值时,它的图象经过原点(2)k为何值时,它的图象经过点(0, -2)(3)k为何值时,它的图象平行直线y=-x(4)k为何值时,它的图象向下平移后,变成直线y=2x+8(5)k为何值时, y随x的增大而减小例1、已知一次函数例2、已知y与x－1成正比例，x=8时，y=6，写出y与x之间函数关系式，并分别求出x=-3时y的值和y =-3时x的值。解：由 y与x－1成正比例可设y=k（x-1）
∵ 当x=8时，y=6 ∴7k=6 ∴
∴ y与x之间函数关系式是：y= （x-1）当x=4时，y= ×（4－1）=当y =-3时，-3= （X－1） X= ② 因为函数图象过点（3，5）和（- 4，-9），则5=3k+b
-9=-4k+bk=2
b=-1例3、已知函数的图象过点（3，5）与（-4，-9），求这个一次函数的解析式。所以函数的解析式为：y=2x-1.解： ①设这个函数的解析式为 (1)先设出函数解析式用待定系数法求函数解析式步骤：（２）根据条件建立含k,b的两个方程（３）解方程组求出待定字母例4、等腰三角形ABC周长为12cm，底边BC长为ycm，腰AB长为xcm.
（1）写出y关于x的函数关系式；
（2）求出x的取值范围；
（3）求出y的取值范围.例5、有两条直线l1:y=ax+b 和l2:y=cx-5,学生甲解出它们的交点为（3，-2）；乙学生因看错c而解出它们的交点为（3/4，1/4），试写出这两条直线的表达式与x轴所围成的三角形面积.例6、小强在劳动技术课中要制作一个周长为80cm的等腰三角形，请你写出底边长ycm与一腰长xcm的函数关系式,并求出自变量x的取值范围.解：y=80-2x
∵两边之和大于第三边且两边之差小于第三边
∴x-x＜y＜x+x
∴0＜80-2x＜2x
即20＜x＜40
∴y=80-2x(20＜x＜40)例７、柴油机在工作时油箱中的余油量Q(千克）与工作时间t（小时）成一次函数关系，当工作开始时油箱中有油40千克，工作3.5小时后，油箱中余油22.5千克： (1)写出余油量Q与时间t的函数关系式；
（2）画出这个函数的图象。解：（１）设Ｑ＝kt＋b。把t=0，Q=40；t=3.5，Q=22.5
分别代入上式，得解得解析式为：Q＝-５t+40　　(0≤t≤8)（２）取t=0，得Q=40；取t=８，得Q=０。描出点
Ａ（０，40），B（8，0）。然后连成线段AB即是所
求的图形。（1）求出函数关系式时，必须找出自变量的取值范围。
（2）画函数图象时，应根据函数自变量的取值范围来确定图象的范围。20图象是包括
两端点的线段..AB(2)求直线关于y轴对称的函数关系式y=－2x+4y=－2x-4y=2x+4例8、已知直线 y=2x－4 (1)求直线关于x轴对称的函数关系式(3)求直线绕原点旋转1800时的函数关系式练一练122.如果要通过平移直线 得到
的图象，那么直线
必须向___平移___个单位.下3、已知函数y=(m+1)x-3
(1)当m取何值时，y随x的增大而增大？这时它的图象经过哪些象限?
(2)当m取何值时，y随x的增大而减小？这时它的图象经过哪些象限?解：当m+1>0即m>-1时y随x的增大而增大，当m+1<0即m<-1时y随x的增大而减小，这时它的图象经过一、三、四象限这时它的图象经过二、三、四象限D-3y12 y2　5、已知一次函数y=kx-k，若y随x的增大而减小，则该函数的图像经过（ ）
A、第一、二、三象限 B、第一、二、四象限
C、第二、三、四象限 D、第一、三、四象限B6、若函数y=kx+b(k,b为常数)的图象如图所示：
(1)那么,当y﹥0时，x的取值范围是(　 )
A、x﹥1　B、x﹥2　C、x﹤1　D、x﹤2(2) 当x＜0时，y的取值范围是（ ）
A．y＞1 B、y＜1
C、1＜y＜0 D．y＜2DA2、已知一次函数y=kx+b(k≠0)在y轴上的截距是-2，且过点(1,3)，求函数解析式。函数解析式为：y=3x+1函数解析式为：y=5x-21、已知一次函数y=kx+b(k≠0)平行于直线y=3x，且过点(1,4)，求函数解析式。3、设点P(3,m),Q(n,2)都在函数y=x+b的图象上,求m+n的值。做一做4、在直角坐标系中，一次函数y＝kx＋b的图像经过三点A（2，0）、B（0，2）、C（m，3），求这个函数的关系式，并求m的值。5、已知一次函数的图像经过点A（2，－1）和点B，其中点B是另一条直线 与y轴的交点，求这个一次函数的表达式。6、已知一次函数 （k，b是常数，且k≠0），x与y的部分对应值如下表所示：
那么不等式 的解集是（　　）
Ａ． Ｂ． Ｃ． Ｄ．D例9、某蔬菜基地要把一批新鲜蔬菜运往外地,有2种方式可供选择,主要参考数据如下:(1)请分别写出汽车,火车运输的总费用y1(元), y2(元),与运输路程x(km)之间的函数关系;(2)你能说出用哪种运输方式好吗?x/kmy/元O20406080100120100400500200300600y1140y2(2)由图象可得:当运输路程小于100km时,用汽车好;当运输路程等于100km时,都一样;当运输路程大于100km时,用火车好.例10、小明家买了一套现价为12万元的房子，购房时已付房款3万元，从第二年起，以后每年付房款5000元与上一年剩余欠款利息的和，已知剩余欠款的年利率为0.4%
1）将第三年，第四年，第十年应付房款填入下列表格中：（2）若第x年（x≥2），小明家应交房款y元，请写出付房款y与x的函数关系式．例11、某公司到果园基地购买某种优质水果，慰问医务工作者，果园基地对购买量在3000kg以上9含3000kg）的有两种销售方案．甲方案：每千克9元，由基地送货上门；乙方案：每千克8元，由顾客自己租车运回．已知该公司租车从基地到公司的运输费为5000元．
⑴分别写出该公司两种购买方案的付款y（元）与所购买的水果量x（千克）之间的函数关系式，并写出自变量x的取值范围；
⑵当购买量在什么范围时，选择哪种购买方案付款最少？并说明理由．1、某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表： 若日销售量y是销售价x的一次函数．
（1）求出日销售量y（件）与销售价x（元）的函数关系式；
（2）求销售价定为30元时，每日的销售利润．练一练2、一次函数y=kx+k过点（1，4），且分别与x轴、y轴交于A、B点，点P（a，0）在x轴正半轴上运动，点Q（0，b）在y轴正半轴上运动，且PQ⊥AB；
（1）求k的值，并在直角坐标系中画出一次函数的图象
（2）求a、b满足的等量关系式；
（3）若△APQ是等腰三角形，
求△APQ的面积。3、平面直角坐标系内有A（2，-1），B（3，3）两点，点P是y轴上一动点，求P到A、B距离之和最小时的坐标．
4、 对于函数 , y的值随x值的____而增大。 5、直线y＝kx+b过点（1，3）和点（－1，1），则
＝__________。6、已知一次函数y=（6+3m）+n-4，n为何值时，函数图象与y轴交点在x轴的下方？ 解：由一次函数当x=1时，y=5；且它的图象与x轴交点
是（６，０），得解得∴一次函数的解析式为y=-x+6。7、已知一次函数y=kx+b(k≠0)在x=1时，y=5，且它的图象与x轴交点的横坐标是６，求这个一次函数的解析式。8、某医药研究所开发了一种新药，在实际验药时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（毫克）随时间x（时）的变化情况如图所示，当成年人按规定剂量服药后。
（1）服药后______时，血液中含药量最高，
达到每毫升_______毫克，接着逐步衰弱。
（2）服药5时，血液中含药量为每毫升____毫克。（3）当x≤2时y与x之间的函数关系式是_____。
（4）当x≥2时y与x之间的函数关系式是____。（5）如果每毫升血液中含药量3毫克或3毫克以上
时，治疗疾病最有效，那么这个有效时间范围是___时。 9、为了适应新课程教学，我校需配置一批电脑。现在有甲、乙两家公司与 我校联系，已知甲公司的报价为每台5800元，优惠条件是购买10台以上则从第11台开始可以按报价的70%计算；乙公司的报价也是5800元，但优惠条件是每台均按报价的85%计算。在电脑品牌、质量等完全相同的前提下，如果让你去购买，你该如何选择？(1)购买不多于10台电脑时，应该选甲还是乙？（2）若购买的台数没有限制,如何选择？请说明理由。y甲=5800×10+ 5800(x-10)·70%y乙=5800x · 85%若y甲 = y乙∴ x=20∴x>20选甲公司或乙公司选乙公司∴10y乙 10、某地市话费收费标准为：通话时间在三分钟以内（包括三分钟），话费为每分钟0.6元；通话时间超过了三分钟，超过部分按每分钟0.2元。则总话费（元）与通话时间x（取整数）之间的关系式为 ：11、某风景区集体门票的收费标准为：20人以内（含20人），每人25元；超过20人，超过部分每人10元，则应收门票y元与游览人数x人之间的关系式为：______________；840某班54名学生去该风景区游览，购买门票共花去______元。 12、为了缓解用电紧张的矛盾，电力公司制定了新的用电收费标准，每月用电量x（千瓦时）与应付电费y（元）的关系如图所示：（1）根据图象求出y与x的函数关系式；
（2）请回答电力公司的收费标准是什么？y=0.5x (0≤x≤50)
y=0.9x-20 (x>50)（1）说出甲、乙两物体的初始位置，并说明开始时谁前谁后？13、已知甲、乙两物体沿同一条直线同时、同向匀速
运动，它们所经过的路程s与所需时间t之间的关系如图
所示.甲物体在离起点2米处，乙物体在起点。甲在前乙在后.（3）求出两图象的交点坐标，并说明实际意义.2秒时乙物体追上甲物体。2秒前甲先乙后
2秒后乙先甲后。（2）分别求出甲、乙的路程s关于时间t的函数解析式.(2,3)（2）用恰当的方式表示费用y与路程s之间的关系。14、某市出租车计费方法如图所示，请根据图象回答下面的问题：（1）出租车的起步价是多少元？在多少路程内只收起步价？（3）起步价里程走完之后，每行驶1km需多少车费？（4）某外地客人坐出租车游览本市，车费为35元，试求出他乘车的里程。15、如图，已知边长为1的正方形OABC在直角坐标系中，A、B两点在第一象限内，OA与X轴的夹角为30°，那么点B的坐标是 （ ， ）。 16、如图，在矩形ABCD中，AB=4，BC=7，P是BC边上与B点不重合的动点，过点P的直线交CD的延长线于R，交AD于Q（Q与D不重合），且∠RPC=45o，设BP=x，梯形ABPQ的面积为y，求y与x之间的函数关系式，并求出自变量x的取值范围。17、某工厂加工一批产品,为了提前交货,规定每个工人完成100个以内,按每个产品2元付酬；超过100个，超过部分每个产品付酬增加0.2元；超过200个，超过部分除按以上规定外，每个产品付酬再增加0.3元，求每个工人：
（1）完成100个以内所得报酬y（元）与产品数x（个）之间的函数关系；
（2）完成100个以上但不超过200个，所得报酬y（元）与产品数x（个）之间的函数关系；
（3）完成200个以上所得报酬y（元）与产品数x（个）之间的函数关系。18、一报刊销售亭从报社订购某晚报的价格是每份0.7元，销售价是每份1元，卖不掉的报纸还可以0.2元的价格退回报社。在一个月内（按30天计算），有20天每天卖出100份，其余10天每天只能卖出60份，但每天报亭从报社订购的份数必须相同。若以报亭每天从报社订购的份数为自变量x，每月所获得的利润y为函数。
（1）写出x与y之间的函数关系式，并指出自变量x的取值范围；
（2）报亭应该每天从报社订购多少份报纸，才能使每月获得的利润最大？最大利润是多少？19、A市和B市分别有某种库存机器12台和6台，现决定支援C村10台，D村8台，已知从A市调运一台机器到C村和D村的运费分别是400元和800元，从B市调运一台机器到C村和D村的运费分别是300元和500元．
(1)设B市运往C村机器x台，求总运费W关于x的函数关系式；
(2)若要求总运费不超过9000元，共有几种调运方案？
(3)求出总运费最低的调运方案，最低运费是多少元？20、某工厂生产某种产品，每件产品的出厂价为50元，其成本价为25元，因为在生产过程中，平均每生产一件产品有0.5立方米污水排出，所以为了净化环境，工厂设计两种对污水进行处理的方案，并准备实施。
方案1:工厂将污水先并净化处理后排出,每处理1立方米污水，所用的原料费为2元,并且每月排污设备损耗费为30000元。
方案2:工厂将污水排放到污水厂统一处理，每处理1立方米污水需付14元的处理费。⑴设工厂每月生产x件产品，每月利润为y元，分别求出施行方案1和方案2时，y与x的函数关系式;(利润＝总收入－总支出)⑵月生产量为6000件产品时，在不污染环境并节约资金的前提下应选哪种处理污水的方案？请通过计算加以说明。y1=(50-25) x -0.5× x × 2 -30000=24 x -30000
y2=(50-25) x -0.5 × x × 14 =18 xy1=24x -30000=24×6000-30000=114000元
y2=18 x =18×6000=108000元再见！