精彩的分形（课题学习）

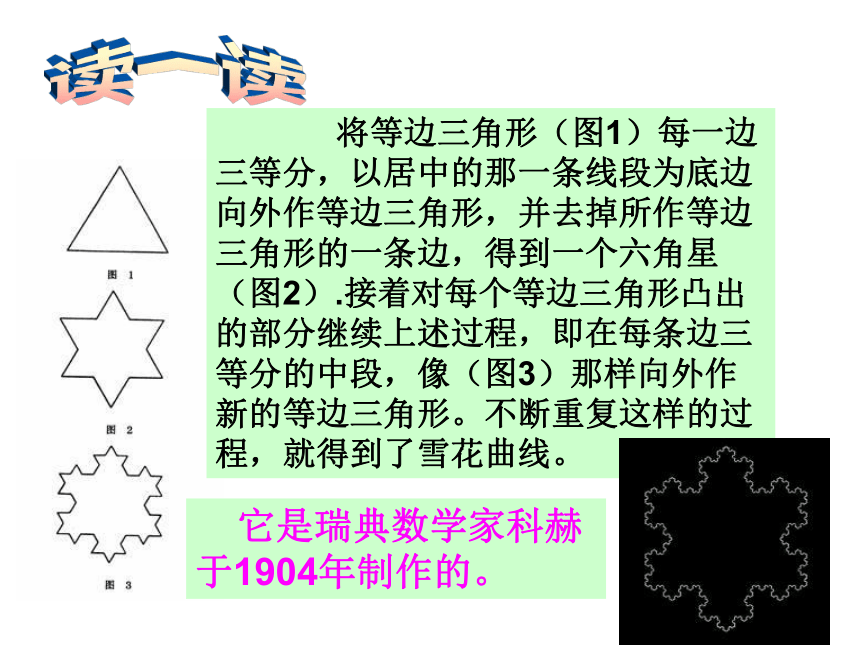
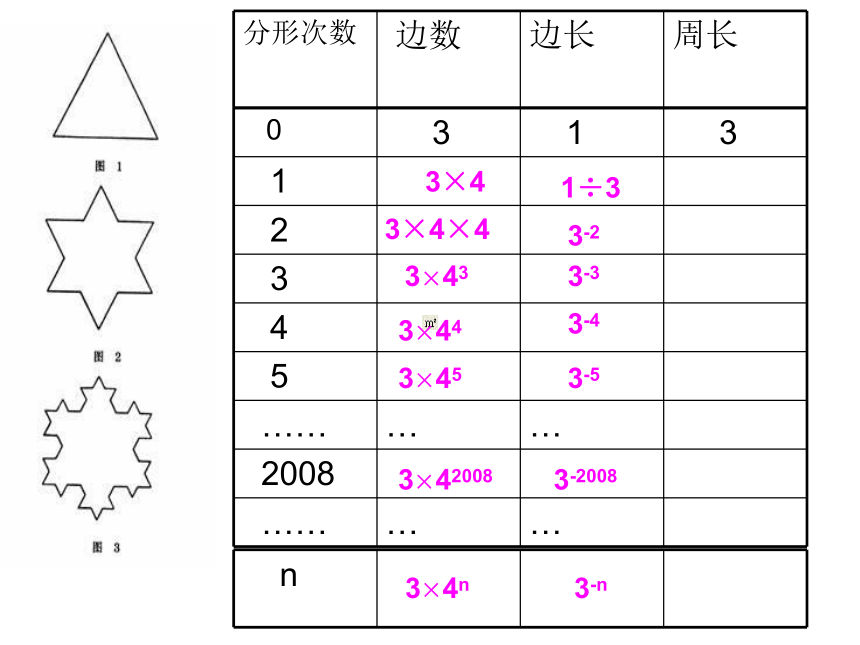
课件29张PPT。精彩的分形课题学习读一读 将等边三角形（图1）每一边三等分，以居中的那一条线段为底边向外作等边三角形，并去掉所作等边三角形的一条边，得到一个六角星（图2）.接着对每个等边三角形凸出的部分继续上述过程，即在每条边三等分的中段，像（图3）那样向外作新的等边三角形。不断重复这样的过程，就得到了雪花曲线。 它是瑞典数学家科赫于1904年制作的。3×41÷33-23×4×43×433-33-43-53-20083-n3×443×453×4n3×42008分形图形的性质：
具有无限的周长，有限的面积。 分形是这样的图形，将其放大后，其结构看起来仍与原先的结构一样，这种现象叫做自相似。分形的创始人是罗德尔 布 罗特于1975年创造。是真正描述大自然的几何学。 分形通常跟分数维，自相似，自组织，非线性系统，混沌等联系起来出现。它是数学的一个分支。我之前说过很多次，数学就是美。而分形的美，更能够被大众所接受，因为它可以通过图形化的方式表达出来。而更由于它美的直观性，被很多艺术家索青睐。分形在自然界里面也经常可以看到，最多被举出来当作分形的例子，就是海岸线，源自于曼德尔布诺特的著名论文《英国的海岸线有多长》。而在生物界，分形的例子也比比皆是。 分形的意义
　　 近20年来，分形的研究受到非常广泛的重视，其原因在于分形既有深刻的理论意义，又有巨大的实用价值。分形向人们展示了一类具有标度不变对称性的新世界，吸引着人们寻求其中可能存在着的新规律和新特征；分形提供了描述自然形态的几何学方法，使得在计算机上可以从少量数据出发，对复杂的自然景物进行逼真的模拟，并启发人们利用分形技术对信息作大幅度的数据压缩。它以其独特的手段来解决整体与部分的关系问题，利用空间结构的对称性和自相似性，采用各种模拟真实图形的模型，使整个生成的景物呈现出细节的无穷回归的性质，丰富多彩，具有奇妙的艺术魅力。 分形对像没有放大极限，无论如何放大，总会看到更详细的结构。借助于分形的计算机生成，从少量的数据生成复杂的自然景物图形，使我们在仿真模拟方面前进了一大步。在分形的诸多研究课题中，分形的计算机生成问题具有明显的挑战性，它使传统数学中无法表达的形态(如山脉、花草等)得以表达，还能生成一个根本“不存在”的图形世界。分形在制造以假乱真的景物方面的进展和潜在的前途，使得无论怎样估计它的影响也不过分。可以肯定，分形图案在自然界真实物体模拟、仿真形体生成、计算机动画、艺术装饰纹理、图案设计和创意
制作等具有广泛的应用价值 。
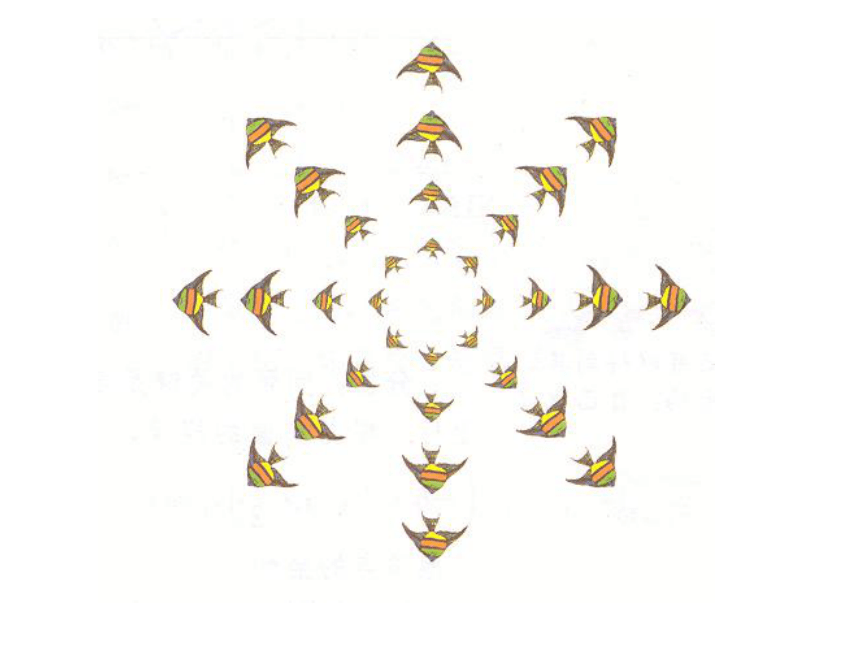
图片欣赏试一试 按课本第127页要求完成“龙”的分形图能工巧匠 自选一个起始图形，设计一个自相似的操作过程，做出一幅美丽的分形图案。