第一章 解直角三角形复习(浙江省湖州市)
图片预览


文档简介
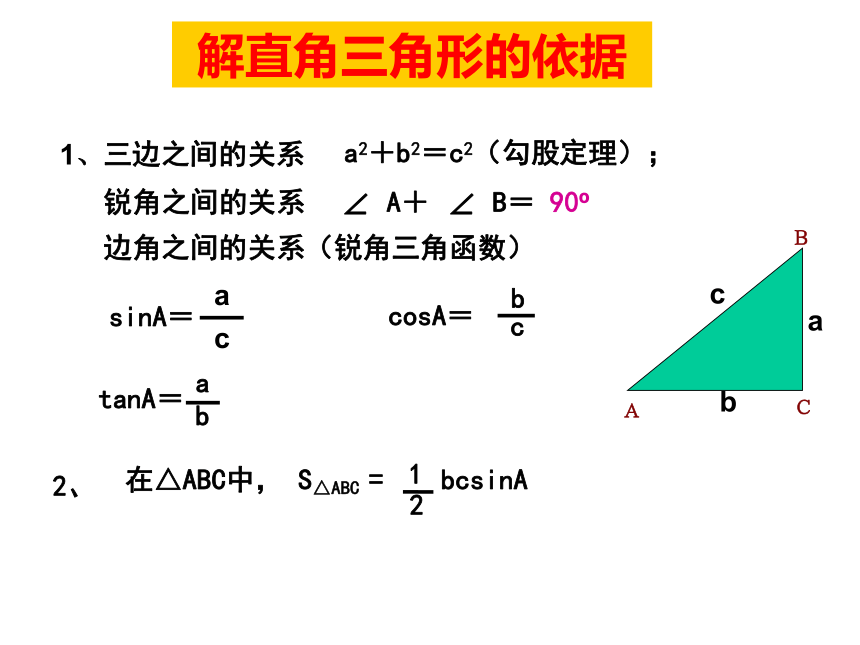
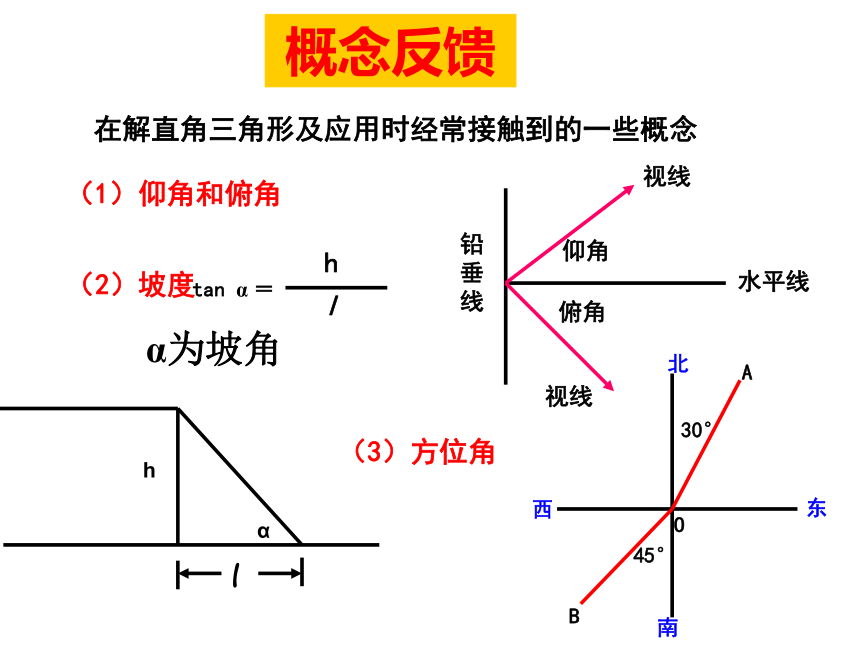
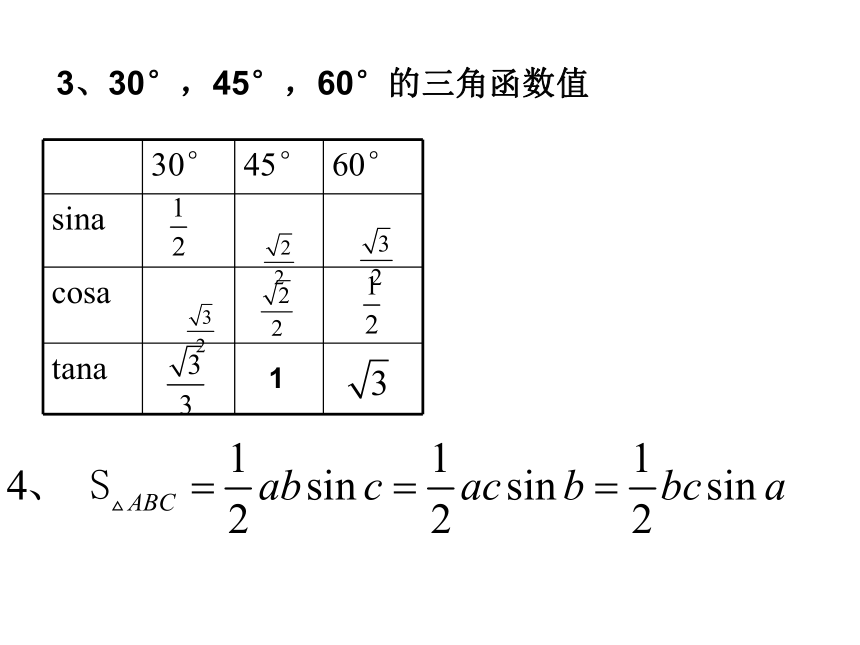
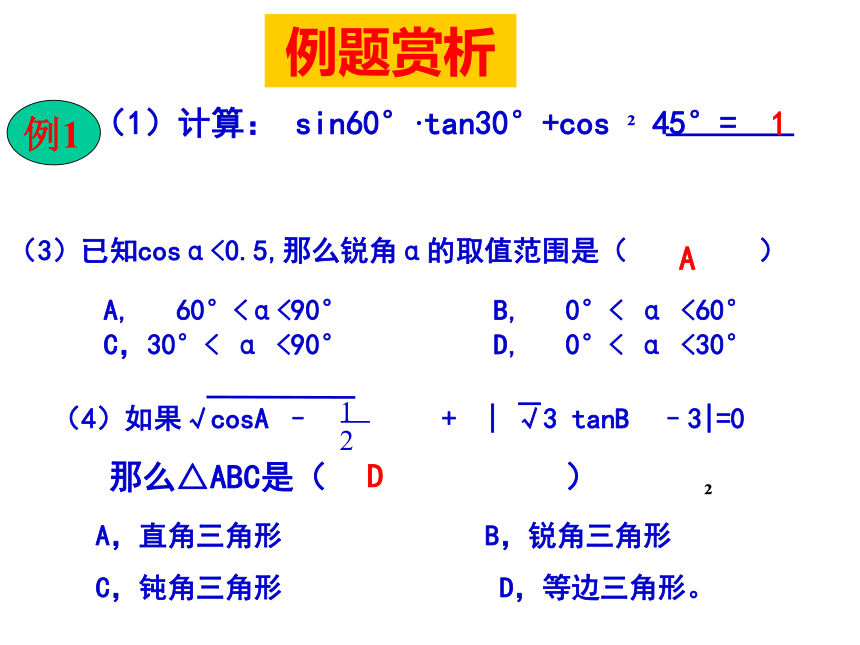
课件20张PPT。第一章 解直角三角形 (复习课) 三边之间的关系a2+b2=c2(勾股定理);锐角之间的关系∠ A+ ∠ B= 90o边角之间的关系(锐角三角函数)sinA=1、解直角三角形的依据在解直角三角形及应用时经常接触到的一些概念概念反馈(1)仰角和俯角(3)方位角α为坡角3、30°,45°,60°的三角函数值11、在Rt△ABC中,∠C=900,a,b,c分别是∠A,∠B,
∠C的对边.(1)已知a=3,b=3,求∠A;
(2)已知c=8,b=4,求a及∠A;;
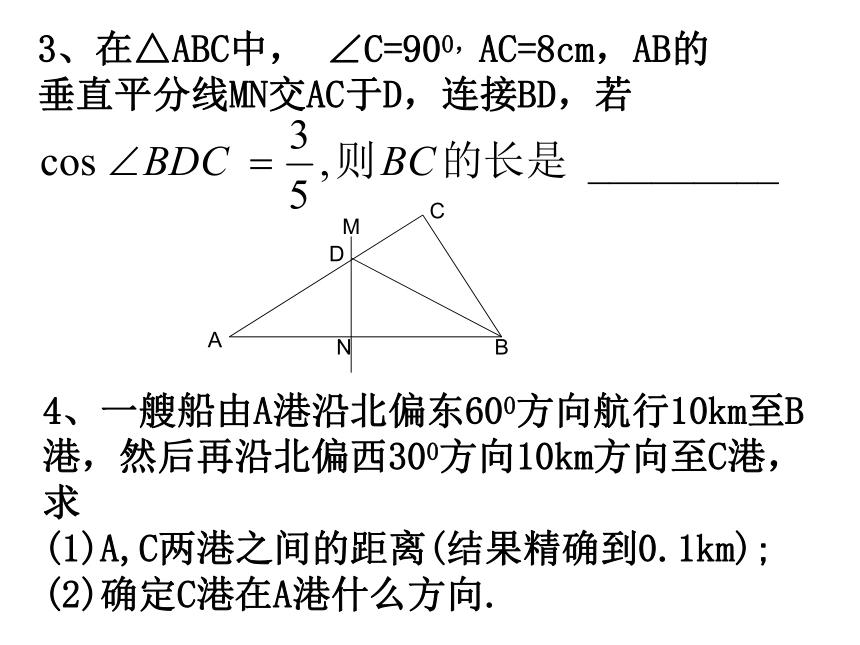
(3)已知c=8,∠A=450,求a及b练一练:2、已知cosA=0.6,求sinA,tanA.3、在△ABC中, ∠C=900,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若ABNCDM4、一艘船由A港沿北偏东600方向航行10km至B港,然后再沿北偏西300方向10km方向至C港,求
(1)A,C两港之间的距离(结果精确到0.1km);
(2)确定C港在A港什么方向.例题赏析(3)已知cosα<0.5,那么锐角α的取值范围是( ) A, 60°<α<90° B, 0°< α <60° C,30°< α <90° D, 0°< α <30°(4)如果√cosA – — + | √3 tanB –3|=012那么△ABC是( ) A,直角三角形 B,锐角三角形
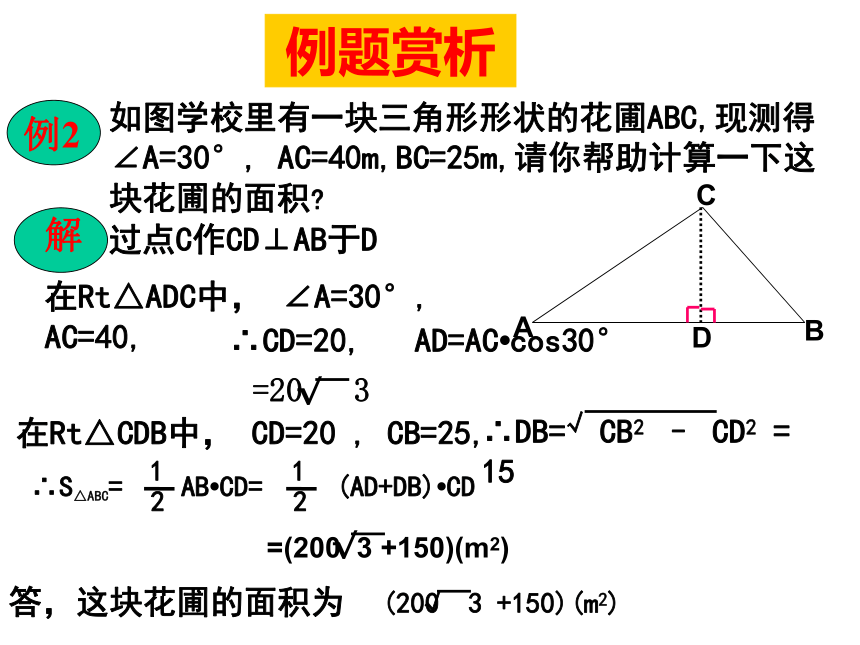
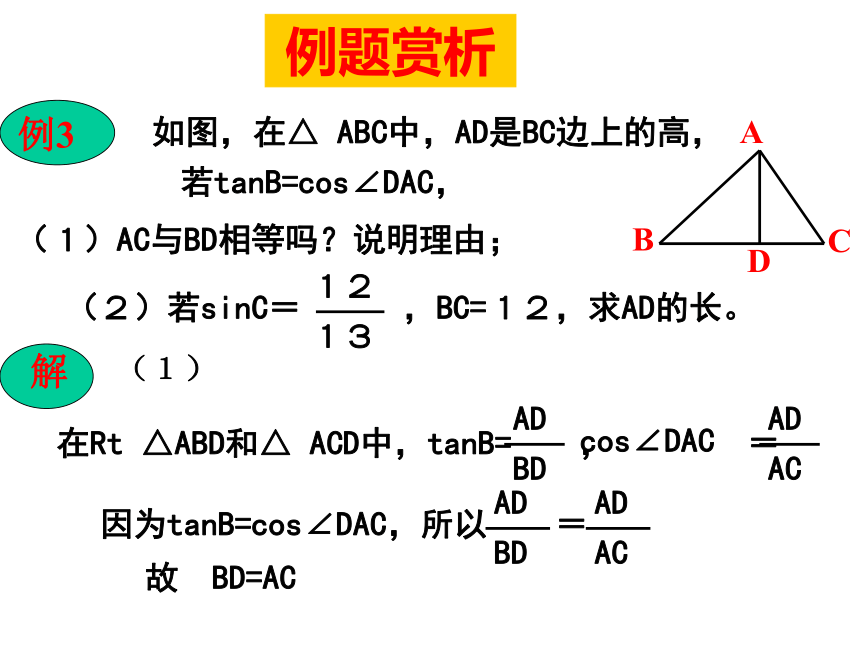
C,钝角三角形 D,等边三角形。1 AD2例题赏析如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,∴CD=20, AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25,例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;故 BD=AC(1)例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;(2)设AC=13k,AD=12k,所以CD=5k,又AC=BD=13k,例题赏析如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?方向,航行24海里到C处,见岛A在北偏西30?方向,货轮继续向西航行,有无触礁的危险?过点A作AD⊥BC于D,设AD=x∵ ∠NBA= 60?, ∠N1BA= 30?,∴ ∠ABC=30?, ∠ACD= 60?,在Rt△ADC中, CD=AD/tan∠ACD= x/tan60?, 在Rt△ADB中, BD=AD/tan30?= x/tan30?, ∵ BD-CD=BC,BC=24 ∴ x/tan30?- x/tan60?=24 答:货轮无触礁危险。当堂训练1,在Rt△ABC中,如果各边都扩大2倍,则锐角A的正
弦值和余弦值( )A,都不变 B,都扩大2倍 C,都缩小2倍 D,不确定。4,如果α和β都是锐角,且sinα= cosβ,
则α与β的关系 是( )A,相等 B,互余 C,互补 D,不确定。A75°BA当堂训练8.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?当堂训练解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中, ∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响当堂训练二解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。9,由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?EF10.如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竹竿长1m处,它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m.这样∠α求就可以算出来了.请你算一算.补充1.一艘轮船在A处观测到东北方向有一小岛C,已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?补充2.(2006新疆)如图,是某市幸福大道上一座人行天桥示意图,天桥的高CO为6米,坡道倾斜角∠CBO=45° ,在距B点5米处有一建筑物DE.为了更加方便行人上、下天桥,市政部门决定减少坡道的倾斜角,但离新坡角A处要留出不少于3米宽的人行道。(1)若将坡道倾斜角改建为30° ( ∠CAO=30° ),那么建筑物DE是否会被拆除?为什么?
(2)若改建坡道后,使人行道的宽恰好为3米,又不拆除建筑物DE,那么坡道的倾斜角应为多少度(精确到1度)?(2006辽宁)如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60° ,沿山坡向上走到P处再测得点C的仰角为45° ,已知OA=100米,山坡坡
度为 ,(即tan∠PAB= )且O、A、B在同一
条直线上。求电视塔OC的高度以及所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)补充3.学习小结一,知识小结:本节课主要复习勾股定理、锐角三角函数、勾股定理在解题中的应用,三角函数在解三角形中的应用。二,方法归纳; 在涉及四边形问题时,经常把四边形进行适当分割,划分为三角形和特殊四边形,再借助特殊四边形的特征和直角三角形知识解决问题。
∠C的对边.(1)已知a=3,b=3,求∠A;
(2)已知c=8,b=4,求a及∠A;;
(3)已知c=8,∠A=450,求a及b练一练:2、已知cosA=0.6,求sinA,tanA.3、在△ABC中, ∠C=900,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若ABNCDM4、一艘船由A港沿北偏东600方向航行10km至B港,然后再沿北偏西300方向10km方向至C港,求
(1)A,C两港之间的距离(结果精确到0.1km);
(2)确定C港在A港什么方向.例题赏析(3)已知cosα<0.5,那么锐角α的取值范围是( ) A, 60°<α<90° B, 0°< α <60° C,30°< α <90° D, 0°< α <30°(4)如果√cosA – — + | √3 tanB –3|=012那么△ABC是( ) A,直角三角形 B,锐角三角形
C,钝角三角形 D,等边三角形。1 AD2例题赏析如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,∴CD=20, AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25,例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;故 BD=AC(1)例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;(2)设AC=13k,AD=12k,所以CD=5k,又AC=BD=13k,例题赏析如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?方向,航行24海里到C处,见岛A在北偏西30?方向,货轮继续向西航行,有无触礁的危险?过点A作AD⊥BC于D,设AD=x∵ ∠NBA= 60?, ∠N1BA= 30?,∴ ∠ABC=30?, ∠ACD= 60?,在Rt△ADC中, CD=AD/tan∠ACD= x/tan60?, 在Rt△ADB中, BD=AD/tan30?= x/tan30?, ∵ BD-CD=BC,BC=24 ∴ x/tan30?- x/tan60?=24 答:货轮无触礁危险。当堂训练1,在Rt△ABC中,如果各边都扩大2倍,则锐角A的正
弦值和余弦值( )A,都不变 B,都扩大2倍 C,都缩小2倍 D,不确定。4,如果α和β都是锐角,且sinα= cosβ,
则α与β的关系 是( )A,相等 B,互余 C,互补 D,不确定。A75°BA当堂训练8.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?当堂训练解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中, ∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响当堂训练二解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。9,由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?EF10.如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竹竿长1m处,它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m.这样∠α求就可以算出来了.请你算一算.补充1.一艘轮船在A处观测到东北方向有一小岛C,已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?补充2.(2006新疆)如图,是某市幸福大道上一座人行天桥示意图,天桥的高CO为6米,坡道倾斜角∠CBO=45° ,在距B点5米处有一建筑物DE.为了更加方便行人上、下天桥,市政部门决定减少坡道的倾斜角,但离新坡角A处要留出不少于3米宽的人行道。(1)若将坡道倾斜角改建为30° ( ∠CAO=30° ),那么建筑物DE是否会被拆除?为什么?
(2)若改建坡道后,使人行道的宽恰好为3米,又不拆除建筑物DE,那么坡道的倾斜角应为多少度(精确到1度)?(2006辽宁)如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60° ,沿山坡向上走到P处再测得点C的仰角为45° ,已知OA=100米,山坡坡
度为 ,(即tan∠PAB= )且O、A、B在同一
条直线上。求电视塔OC的高度以及所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)补充3.学习小结一,知识小结:本节课主要复习勾股定理、锐角三角函数、勾股定理在解题中的应用,三角函数在解三角形中的应用。二,方法归纳; 在涉及四边形问题时,经常把四边形进行适当分割,划分为三角形和特殊四边形,再借助特殊四边形的特征和直角三角形知识解决问题。
