3.2实数

课件12张PPT。实数———浙教版 七年级上册
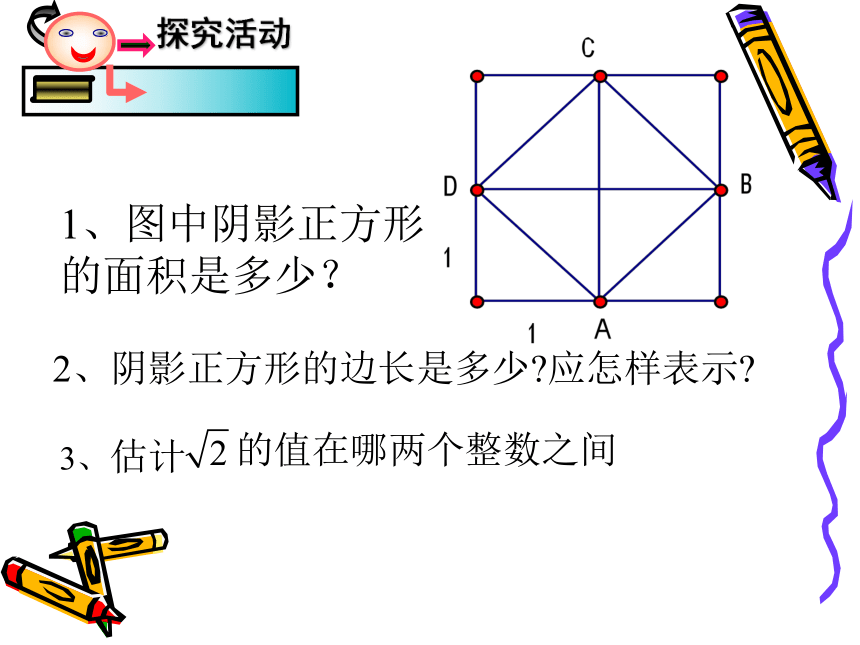
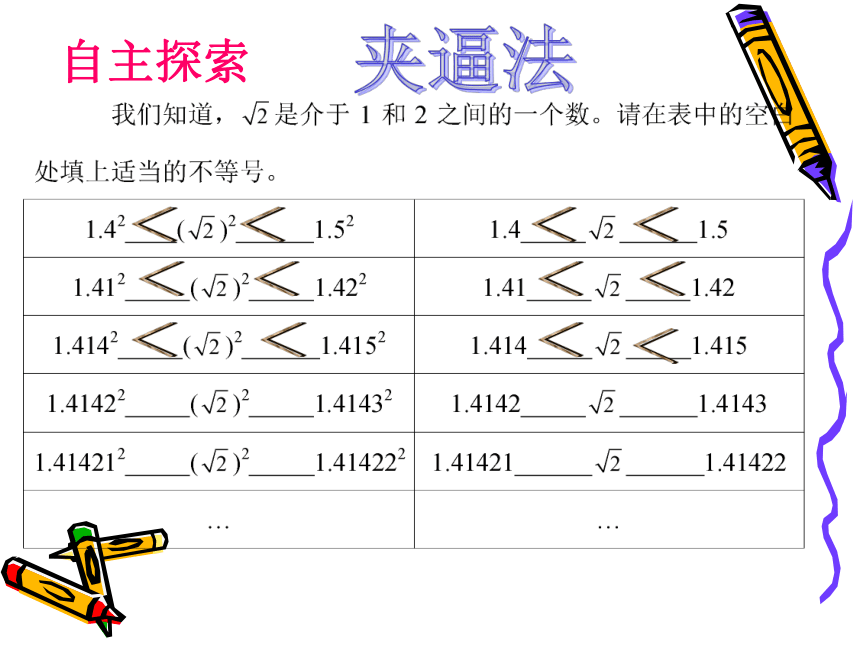
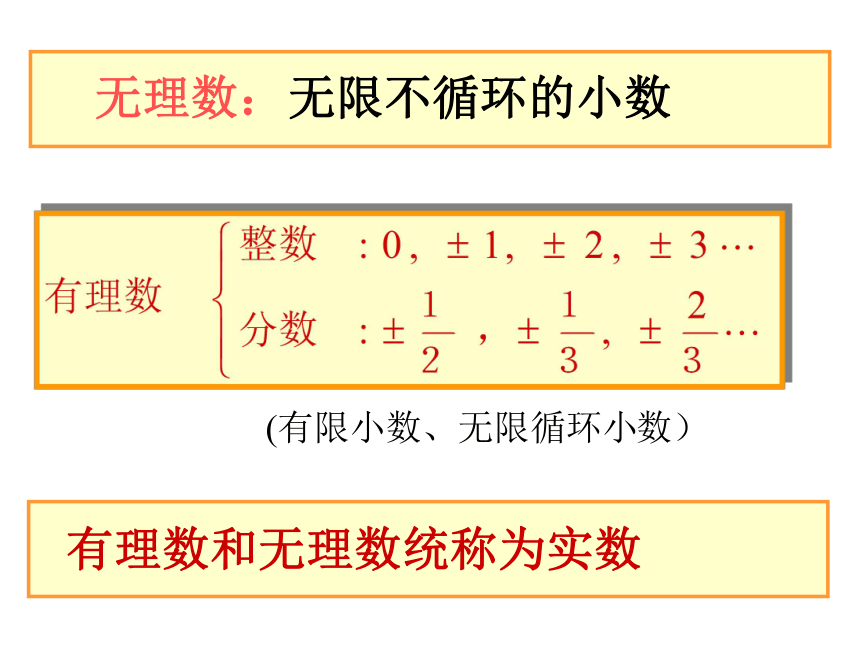
雁湖九年一贯制学校七(2)班1、图中阴影正方形的面积是多少？3、估计的值在哪两个整数之间2、阴影正方形的边长是多少?应怎样表示?自主探索<<<<<<<<<<<<夹逼法用“夹逼法”，可以得到一系列越来越接近的近似值：=1.414 213 562 373 095 048 801 688 724 209 6…那它是什么数呢？是整数吗？是分数吗？它不是有理数！像这种无限不循环小数叫做无理数。如：1.010010001…（两个“１”之间依次多一个“０”）都是无理数无限不循环的小数无理数：二、想一想　把书从有理数扩充到实数以后，有理数中的相反数和绝对值的概念同样能运用于实数吗？
　有理数的大小比较的方法可以推广到实数吗？填空：
（1）－　　的相反数是_________;
(2)　　　　　 =_______;
(3)一个数的绝对值是　　,则这个数是___________.
（４）比较大小：三、做一做有理数和无理数之战
　　在一个早晨，同学小雨一觉醒来，发现窗户外的山坡上在打仗。仔细一看，一边打着“有理数”的大旗子，一边打着“无理数”的大旗子。
　　有理数和无理数为什么要打仗？哦，原来是为了名字。
　　听听无理数司令　　　怎么说：“我们无理数和有理数同样是数，为什么他们‘有理’，我们‘无理’？我们究竟哪点儿无理？”
　　对呀！无理怎么会存在嘛！小雨心里也在琢磨。
　　“因为人们最开始发现的是有理数，见到我们无理数时还不理解，所以取了‘无理数’这么难听的名字。可是现在，人们已经充分认识我们了，就该给我们摘掉‘无理’的帽子才对！”四、听一听五、说一说（１）听了上面这则故事，你认为它们的根本区别在哪里？
（２）实数与数轴上的点有怎样的关系？ 2600多年前，古希腊的毕达哥拉斯学派，非常崇拜数。认为“万物的本质都是数”，他们企图用数来解释一切。毕达哥拉斯学派有个叫希伯斯的年轻人，他对正方形的对角线问题很感兴趣。他根据勾股定理发现，正方形的对角线长和边长之比不能用整数比来表示。
这一发现，动摇了毕达哥拉斯学派的哲学基础，使他们大为惊恐，他们严密封锁希伯斯的发现，并规定谁要是泄露出去，就要处以极刑。
后来希伯斯还是把自己的发现传了出去，但他又十分害怕，就逃往家乡，想不到在他渡地中海时，被毕达哥拉斯学派的信徒追上，并把他投到海里，杀害了他。
无理数的发现。曾在西方引起了数学危机，然而在我国，对于古代希腊认为迷惑不解的开方不尽之数，早在公元1世纪的《九章算术》与随后的《九章算术列注》中就直截了当地“以面命之”，给出了独立成数的定义与某些运算法则，从而构成了整个实数系统。在《九章算术》里还介绍笔算开平方，国外直到公元5世纪才有开平方法的介绍。同学们再见