4.2相似三角形(浙江省湖州市长兴县)

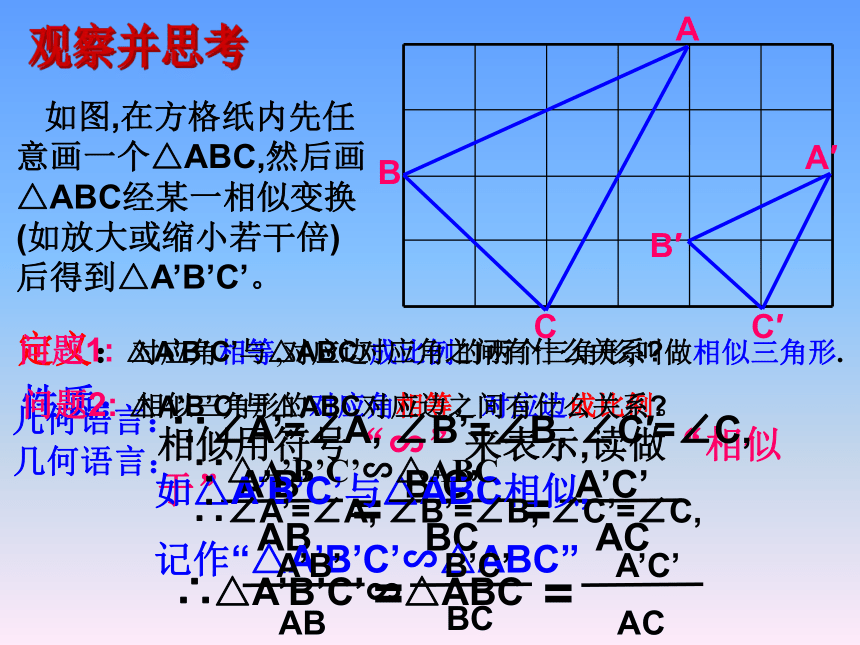
课件17张PPT。3.3圆心角(1)4.2 相似三角形泗安中学 唐 君问题1：这两个三角形是否为相似形？观察下图中两幅图形的形状和大小有什么关系？相似形定义：我们把形状相同的两个图形称为相似形。几何语言：相似用符号“∽”来表示,读做“相似于”性质：相似三角形的对应角相等，对应边成比例。观察并思考 如图,在方格纸内先任意画一个△ABC,然后画△ABC经某一相似变换(如放大或缩小若干倍)后得到△A’B’C’。定义：对应角相等,对应边成比例的两个三角形,叫做相似三角形.∴△A’B’C’∽△ABC如△A’B’C’与△ABC相似,
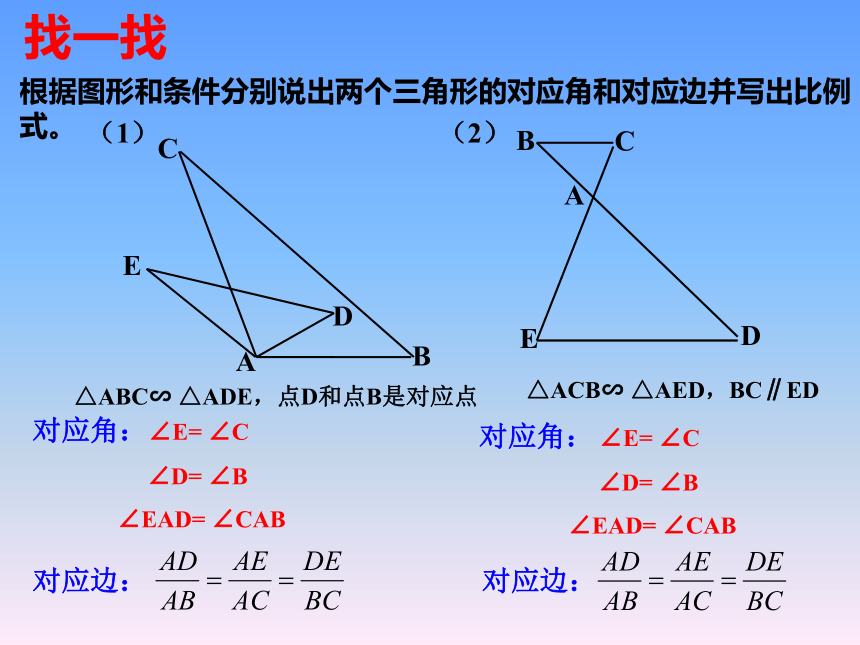
记作“△A’B’C’∽△ABC”∵△A’B’C’∽△ABC几何语言：问题1: △A’B’C’与△ABC对应角之间有什么关系?问题2: △A’B’C’与△ABC对应边之间有什么关系?根据图形和条件分别说出两个三角形的对应角和对应边并写出比例式。找一找 ∠E= ∠C
∠D= ∠B
∠EAD= ∠CAB对应边： ∠E= ∠C
∠D= ∠B
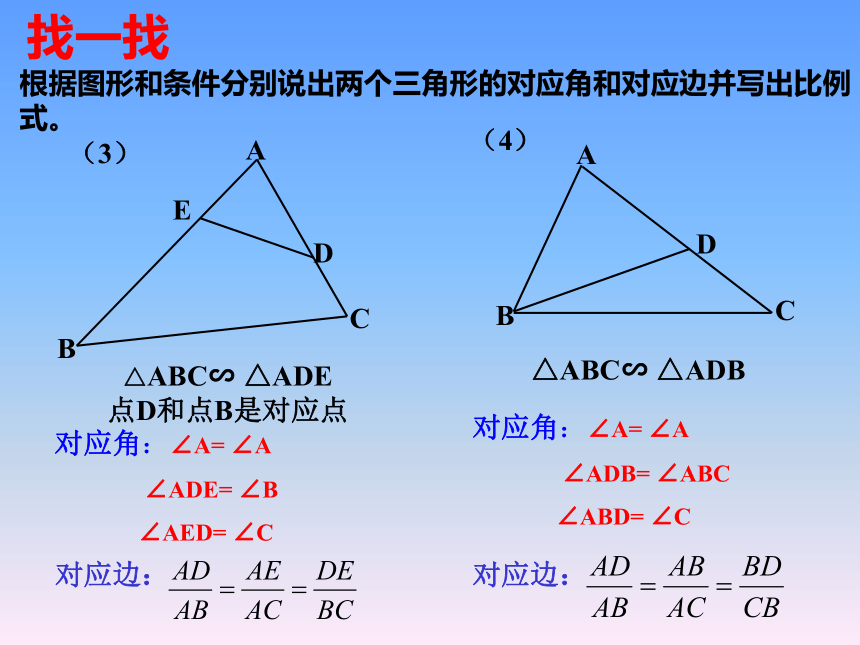
∠EAD= ∠CAB对应边：对应角：对应角：根据图形和条件分别说出两个三角形的对应角和对应边并写出比例式。对应角：∠A= ∠A
∠ADE= ∠B
∠AED= ∠C对应边：对应角：∠A= ∠A
∠ADB= ∠ABC
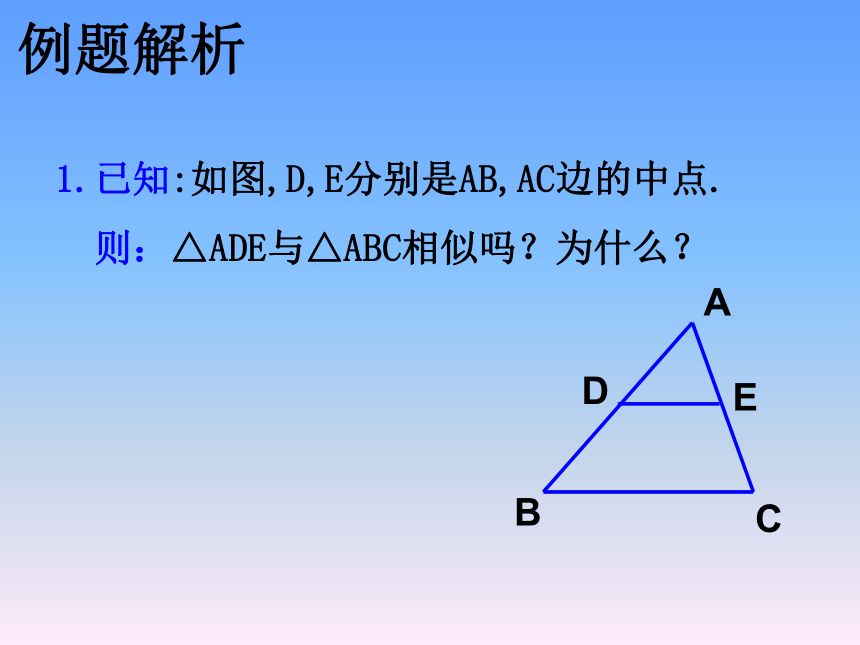
∠ABD= ∠C对应边：找一找 1.已知:如图,D,E分别是AB,AC边的中点.
则：△ADE与△ABC相似吗？为什么？例题解析（4）两个全等三角形一定相似。 （ ）（3）两个等边三角形一定相似。 （ ）辩一辩：（1）两个直角三角形一定相似。 （ ）（2）两个等腰三角形一定相似。 （ ）那么△ABC与△DEF对应边的比= ？ 相似三角形的对应角相等,对应边成比例.性质: 相似三角形对应边的比,叫做两个相似三角形的相似比(或相似系数)。相似比用k表示 即:△ABC与△DEF的相似比k1 = △DEF 与△ABC的相似比k2=练一练: 1.若△ABC与 DEF的相似比为2：5,则△ DEF与 △ ABC的相似
比为 。 5:2 2.在△ABC中，BC=54，CA=45，AB=63。另一个和它相似的
三角形的最短边是15，则它的最长边一定是（ ）
A 18 B 21 C 24 D 19.5 3. △ABC∽△ A′B′C′, ∠A=45 °， ∠B=105°，则
∠ C′等于（ ）度
A 45 B 105 C 80 D 30 BD4.下图中△ABC与△DEF 相似，你能确定出m与x的值吗？练一练例2、如图(1),D,E分别是△ABC的边AB,AC所在直线上的点, 点D与点B是对应点.△ADE ∽△ABC.已知AD﹕AB=1﹕2,BC=9cm,求DE的长.变式1、如图(2),D,E分别是△ABC的边AB,AC上的点,点D与点B是对应点. △ADE∽△ABC.已知AD﹕DB=1﹕2,BC=9cm求DE的长.变式2：如图(3),D,E分别是△ABC的AB,AC边上的点，△ADE∽△ACB.∠ADE＝∠CAD＝2 cm,DB＝4 cm,AC＝10cm,求AE的长. 如图,D是AB上一点, △ABC∽△ADB,∠ADB=65°
∠C=43°
(1)求∠ABD, ∠ABC的度数;
(2) 若AD＝2 cm, AB=3 cm ，求AC的长变式3小明打算制作两个相似的三角形框架，
其中一个三角形框架的三边长分别为4，6，9。
已知另一个三角形一条边长度为3，
则余下的那两条边的长度，你能帮助他确定吗？探索与思考体会.分享 请你谈谈对相似三角形的认识，让大家与你分享吧!对应角相等对应边成比例——“∽”k≠1 两个形状相同，大小不等的相似三角形k=1 两个全等三角形，是相似三角形的特例相似三角形定义相似比
（对应边的比值）
表示法一、基本知识： 1、寻找对应边的方法2、利用相似三角形的性质求角度或者线段长。 边的大小对应角的对边二、基本方法：（数形结合、分类讨论）收 获布 置 作 业1、数学作业本（1）P26-27
2、选做题：
如图，在△ABC中，D、E、F分别是AB、
AC、BC边上的中点
则：（1）图中有几对相似三角形？
（2）若△DEF∽ △CBA，请说明理由。谢谢光临，多多指教祝同学们学习进步！