浙教版八年级数学上册试题 2.7 探索勾股定理(含答案)
文档属性
| 名称 | 浙教版八年级数学上册试题 2.7 探索勾股定理(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 112.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 12:02:12 | ||
图片预览




文档简介
2.7 探索勾股定理
一.选择题
1.在Rt△ABC中,∠C=90°,a=6,b=8,则c的长为( )
A.14 B.12 C.10 D.7
2.满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.AC=1,BC=2,
C.AC=6,BC=8,AB=10 D.,,
3.已知Rt△ABC中,∠C=90°.若a+b=14cm,c=12cm,则Rt△ABC的面积是( )
A.13cm2 B.26cm2 C.48cm2 D.52cm2
4.如图是一棵勾股树,它是由正方形和直角三角形拼成的,若正方形A、B、C、D的边长分别是4、5、3、4,则最大正方形E的面积是( )
A.66 B.16 C.32 D.2306
5.如图,在△ABC中,点D是AB中点,BE⊥AC垂足为E,连接DE,若∠ABE=30°,∠C=45°,DE=2,则BC的长为( )
A.2 B.3 C.2 D.2
6.已知三角形的两边分别为3、4,要使该三角形为直角三角形,则第三边的长为( )
A.5 B. C.5或 D.3或4
7.校园内有两棵树,相距8米,一棵树高为13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞( )
A.10米 B.11米 C.12米 D.13米
8.如图,“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成大正方形,若小正方形边长为1,大正方形边长为5,则一个直角三角形的周长是( )
A.6 B.7 C.12 D.15
9.如图,“赵爽弦图”由4个全等的直角三角形所围成,在Rt△ABC中,AC=b,BC=a,∠ACB=90°,若图中大正方形的面积为48,小正方形的面积为6,则(a+b)2的值为( )
A.60 B.79 C.84 D.90
10.已知a,b,c是三角形的三边长,如果满足,则三角形的形状是( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.钝角三角形
二.填空题
11.△ABC中,AB=AC,BC=4cm,若AD是BC上的高,且AD=4cm.则AB的长为 cm.
12.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=2,BC=,则CD为 .
13.如图所示,∠ABC=∠BAD=90°,AC=13,BC=5,AD=16,则BD的长为 .
14.如图,在四边形ABCD中,AB=1,BC=1,CD=2,DA=且∠ABC=90°,则四边形ABCD的面积是 .
15.若△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b﹣c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13.其中能判断△ABC是直角三角形的是_____(填序号).
16.已知△ABC是边长为6的等边三角形,过点B作AC的垂线l,垂足为D,点P为直线l上的点,作点A关于CP的对称点Q,当△ABQ是等腰三角形时,PD的长度为 .
17.课本中有这样的一句话:“利用勾股定理可以作出,,…等线段”(如图所示),即:OA=1,过点A作AA1⊥OA且AA1=1,根据勾股定理,得OA1=;再过点A1作A1A2⊥OA1,且A1A2=1,得OA2=;…,以此类推,OA2020= .
三.解答题
18.如图,在△ABC中,D是AB的中点,AC=2,BC=2,AB=2,延长AC
到E,使得CE=CD,连接BE.
(1)求证:∠ACB=90°;
(2)求线段BE的长度.
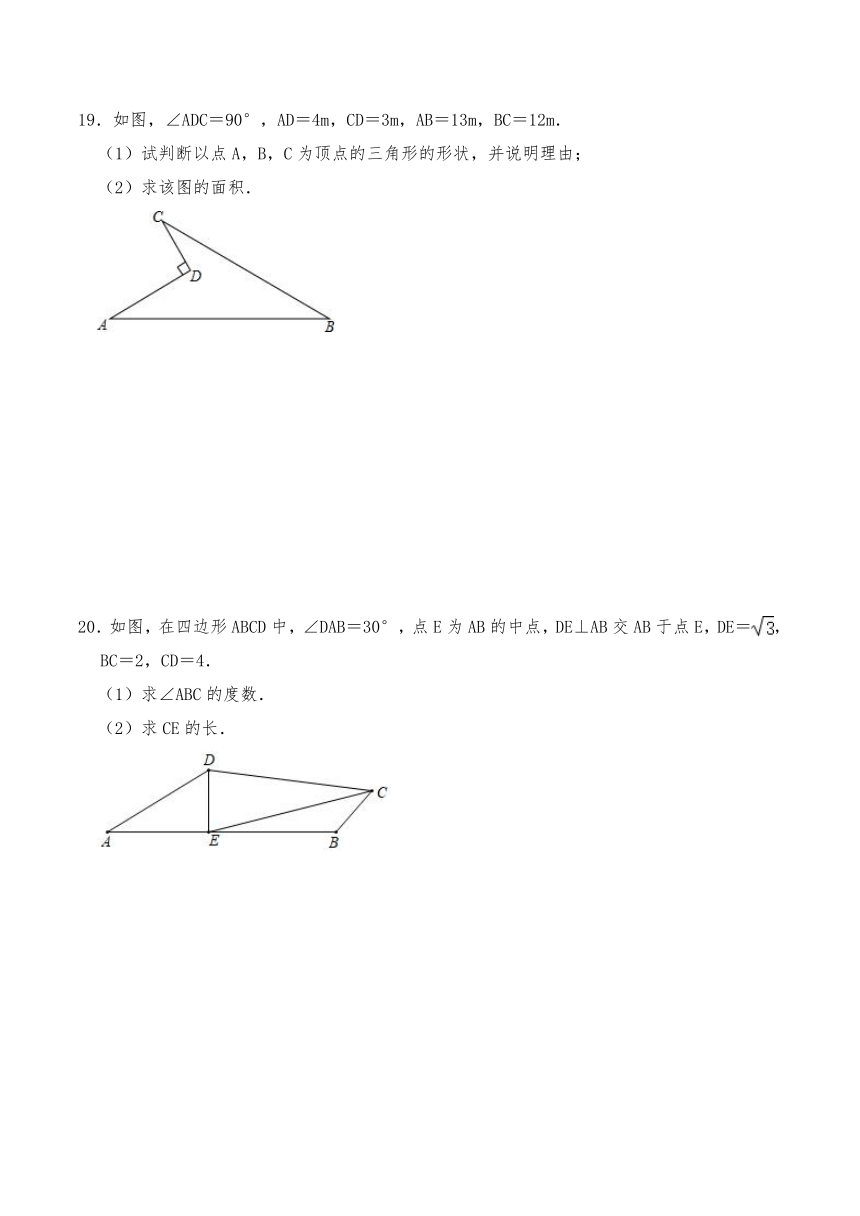
19.如图,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m.
(1)试判断以点A,B,C为顶点的三角形的形状,并说明理由;
(2)求该图的面积.
20.如图,在四边形ABCD中,∠DAB=30°,点E为AB的中点,DE⊥AB交AB于点E,DE=,BC=2,CD=4.
(1)求∠ABC的度数.
(2)求CE的长.
21.(1)在Rt△ABC中,∠C=90°,BC=2,AB=,求AC的长;
(2)已知△ABC中,BC=1,AC=,AB=2,求证:△ABC是直角三角形.
22.如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16.
(1)求证:BD⊥AC;
(2)若E是边AB上的动点,求线段DE的最小值.
23.如图,在笔直的高速路旁边有A、B两个村庄,A村庄到公路的距离AC=8km,B村庄到公路的距离BD=14km,测得C、D两点的距离为20km,现要在CD之间建一个服务区E,使得A、B两村庄到E服务区的距离相等,求CE的长.
24.如图,在四边形ABFC中,∠ABC=90°,CD⊥AD,AD2=2AB2﹣CD2.求证:AB=BC.
答案
一.选择题
C.D.A.A.D.C.A.C.D.A.
二.填空题
11.2.
12.2.
13.20.
14.+.
15.①②④.
16.3或6﹣3或或3+6.
17..
三.解答题
18.(1)证明:∵在△ABC中,AC=2,BC=2,AB=2,
∴AC2=4,BC2=8,AB2=12,
∴AC2+BC2=AB2.
∴∠ACB=90°;
(2)由(1)知,∠ACB=90°,则∠BCE=90°.
∵D是AB的中点,AB=2,CE=CD,
∴CE=CD=AB=.
∴在直角△BCE中,由勾股定理得:BE===.
19.解:(1)以点A,B,C为顶点的三角形的形状是直角三角形,
理由是:
∵∠ADC=90°,AD=4m,CD=3m,
∴由勾股定理得:AC==5cm,
∵AB=13m,BC=12m,
∴AC2+BC2=AB2,
∴∠ACB=90°,
即以点A,B,C为顶点的三角形的形状是直角三角形;
(2)图形的面积S=S△ACB﹣S△ADC===24(cm)2.
20.解:(1)连接BD,作CF⊥AB于F,如图所示:
则∠BFC=90°,
∵点E为AB的中点,DE⊥AB,
∴BD=AD,AE=BE,
∵∠DAB=30°,
∴∠DBE=∠DAB=30°,BD=AD=2DE=2,AE=BE=DE=3,
∵BC2+BD2=22+(2)2=16=CD2,
∴△BCD是直角三角形,∠CBD=90°,
∴∠ABC=∠ABD+∠CBD=30°+90°=120°;
(2)由(1)可得:∠CBF=180°﹣30°﹣90°=60°,
∴∠BCF=30°,∠BFC=90°,
∴∠BCF=30°,
∴BF=BC=1,CF=BF=,
∴EF=BE+BF=4,
在Rt△CEF中,由勾股定理得:CE==.
21.(1)解:∵Rt△ABC中,∠C=90°,BC=2,AB=,
∴AC=,
==,
=3.
(2)证明:∵在△ABC中,BC=1,AC=,AB=2,
BC2+AC2=12+()2=4=22=AB2,
∴∠C=90°,
∴△ABC为直角三角形.
22.解:(1)∵AC=21,AD=16,
∴CD=AC﹣AD﹣5,
∵BD2+CD2=122+52=169=BC2,
∴∠BDC=90°,
∴BD⊥AC.
(2)当DE⊥AB时,DE最短,
∵AB===20,
∵ AD DB= AB DE,
∴DE==9.6,
∴线段DE使得最小值为9.6.
23.解:设CE=x,则DE=20﹣x,
由勾股定理得:
在Rt△ACE中,AE2=AC2+CE2=82+x2,
在Rt△BDE中,BE2=BD2+DE2=142+(20﹣x)2,
由题意可知:AE=BE,
所以:82+x2=142+(20﹣x)2,解得:x=13.3
所以,E应建在距C点13.3km,
即CE=13.3km.
24.证明:∵在△ABC中,∠ABC=90°,
∴AB2+BC2=AC2.
∵在△ACD中,CD⊥AD,
∴AD2+CD2=AC2,
∴AB2+BC2=AD2+CD2,
又AD2=2AB2﹣CD2,
∴AB2+BC2=2AB2﹣CD2+CD2,
即AB2=BC2,
∴AB=BC.
一.选择题
1.在Rt△ABC中,∠C=90°,a=6,b=8,则c的长为( )
A.14 B.12 C.10 D.7
2.满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.AC=1,BC=2,
C.AC=6,BC=8,AB=10 D.,,
3.已知Rt△ABC中,∠C=90°.若a+b=14cm,c=12cm,则Rt△ABC的面积是( )
A.13cm2 B.26cm2 C.48cm2 D.52cm2
4.如图是一棵勾股树,它是由正方形和直角三角形拼成的,若正方形A、B、C、D的边长分别是4、5、3、4,则最大正方形E的面积是( )
A.66 B.16 C.32 D.2306
5.如图,在△ABC中,点D是AB中点,BE⊥AC垂足为E,连接DE,若∠ABE=30°,∠C=45°,DE=2,则BC的长为( )
A.2 B.3 C.2 D.2
6.已知三角形的两边分别为3、4,要使该三角形为直角三角形,则第三边的长为( )
A.5 B. C.5或 D.3或4
7.校园内有两棵树,相距8米,一棵树高为13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞( )
A.10米 B.11米 C.12米 D.13米
8.如图,“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成大正方形,若小正方形边长为1,大正方形边长为5,则一个直角三角形的周长是( )
A.6 B.7 C.12 D.15
9.如图,“赵爽弦图”由4个全等的直角三角形所围成,在Rt△ABC中,AC=b,BC=a,∠ACB=90°,若图中大正方形的面积为48,小正方形的面积为6,则(a+b)2的值为( )
A.60 B.79 C.84 D.90
10.已知a,b,c是三角形的三边长,如果满足,则三角形的形状是( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.钝角三角形
二.填空题
11.△ABC中,AB=AC,BC=4cm,若AD是BC上的高,且AD=4cm.则AB的长为 cm.
12.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=2,BC=,则CD为 .
13.如图所示,∠ABC=∠BAD=90°,AC=13,BC=5,AD=16,则BD的长为 .
14.如图,在四边形ABCD中,AB=1,BC=1,CD=2,DA=且∠ABC=90°,则四边形ABCD的面积是 .
15.若△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b﹣c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13.其中能判断△ABC是直角三角形的是_____(填序号).
16.已知△ABC是边长为6的等边三角形,过点B作AC的垂线l,垂足为D,点P为直线l上的点,作点A关于CP的对称点Q,当△ABQ是等腰三角形时,PD的长度为 .
17.课本中有这样的一句话:“利用勾股定理可以作出,,…等线段”(如图所示),即:OA=1,过点A作AA1⊥OA且AA1=1,根据勾股定理,得OA1=;再过点A1作A1A2⊥OA1,且A1A2=1,得OA2=;…,以此类推,OA2020= .
三.解答题
18.如图,在△ABC中,D是AB的中点,AC=2,BC=2,AB=2,延长AC
到E,使得CE=CD,连接BE.
(1)求证:∠ACB=90°;
(2)求线段BE的长度.
19.如图,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m.
(1)试判断以点A,B,C为顶点的三角形的形状,并说明理由;
(2)求该图的面积.
20.如图,在四边形ABCD中,∠DAB=30°,点E为AB的中点,DE⊥AB交AB于点E,DE=,BC=2,CD=4.
(1)求∠ABC的度数.
(2)求CE的长.
21.(1)在Rt△ABC中,∠C=90°,BC=2,AB=,求AC的长;
(2)已知△ABC中,BC=1,AC=,AB=2,求证:△ABC是直角三角形.
22.如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16.
(1)求证:BD⊥AC;
(2)若E是边AB上的动点,求线段DE的最小值.
23.如图,在笔直的高速路旁边有A、B两个村庄,A村庄到公路的距离AC=8km,B村庄到公路的距离BD=14km,测得C、D两点的距离为20km,现要在CD之间建一个服务区E,使得A、B两村庄到E服务区的距离相等,求CE的长.
24.如图,在四边形ABFC中,∠ABC=90°,CD⊥AD,AD2=2AB2﹣CD2.求证:AB=BC.
答案
一.选择题
C.D.A.A.D.C.A.C.D.A.
二.填空题
11.2.
12.2.
13.20.
14.+.
15.①②④.
16.3或6﹣3或或3+6.
17..
三.解答题
18.(1)证明:∵在△ABC中,AC=2,BC=2,AB=2,
∴AC2=4,BC2=8,AB2=12,
∴AC2+BC2=AB2.
∴∠ACB=90°;
(2)由(1)知,∠ACB=90°,则∠BCE=90°.
∵D是AB的中点,AB=2,CE=CD,
∴CE=CD=AB=.
∴在直角△BCE中,由勾股定理得:BE===.
19.解:(1)以点A,B,C为顶点的三角形的形状是直角三角形,
理由是:
∵∠ADC=90°,AD=4m,CD=3m,
∴由勾股定理得:AC==5cm,
∵AB=13m,BC=12m,
∴AC2+BC2=AB2,
∴∠ACB=90°,
即以点A,B,C为顶点的三角形的形状是直角三角形;
(2)图形的面积S=S△ACB﹣S△ADC===24(cm)2.
20.解:(1)连接BD,作CF⊥AB于F,如图所示:
则∠BFC=90°,
∵点E为AB的中点,DE⊥AB,
∴BD=AD,AE=BE,
∵∠DAB=30°,
∴∠DBE=∠DAB=30°,BD=AD=2DE=2,AE=BE=DE=3,
∵BC2+BD2=22+(2)2=16=CD2,
∴△BCD是直角三角形,∠CBD=90°,
∴∠ABC=∠ABD+∠CBD=30°+90°=120°;
(2)由(1)可得:∠CBF=180°﹣30°﹣90°=60°,
∴∠BCF=30°,∠BFC=90°,
∴∠BCF=30°,
∴BF=BC=1,CF=BF=,
∴EF=BE+BF=4,
在Rt△CEF中,由勾股定理得:CE==.
21.(1)解:∵Rt△ABC中,∠C=90°,BC=2,AB=,
∴AC=,
==,
=3.
(2)证明:∵在△ABC中,BC=1,AC=,AB=2,
BC2+AC2=12+()2=4=22=AB2,
∴∠C=90°,
∴△ABC为直角三角形.
22.解:(1)∵AC=21,AD=16,
∴CD=AC﹣AD﹣5,
∵BD2+CD2=122+52=169=BC2,
∴∠BDC=90°,
∴BD⊥AC.
(2)当DE⊥AB时,DE最短,
∵AB===20,
∵ AD DB= AB DE,
∴DE==9.6,
∴线段DE使得最小值为9.6.
23.解:设CE=x,则DE=20﹣x,
由勾股定理得:
在Rt△ACE中,AE2=AC2+CE2=82+x2,
在Rt△BDE中,BE2=BD2+DE2=142+(20﹣x)2,
由题意可知:AE=BE,
所以:82+x2=142+(20﹣x)2,解得:x=13.3
所以,E应建在距C点13.3km,
即CE=13.3km.
24.证明:∵在△ABC中,∠ABC=90°,
∴AB2+BC2=AC2.
∵在△ACD中,CD⊥AD,
∴AD2+CD2=AC2,
∴AB2+BC2=AD2+CD2,
又AD2=2AB2﹣CD2,
∴AB2+BC2=2AB2﹣CD2+CD2,
即AB2=BC2,
∴AB=BC.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
