浙江版八年级数学上册试题 2.8 直角三角形全等的判定-浙教版(含答案)
文档属性
| 名称 | 浙江版八年级数学上册试题 2.8 直角三角形全等的判定-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 104.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 12:49:53 | ||
图片预览




文档简介
2.8 直角三角形全等的判定
一.选择题
1.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.∠BAC=∠BAD B.AC=AD
C.∠ABC=∠ABD D.以上都不正确
2.下列判定直角三角形全等的方法,不正确的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.斜边和一直角边对应相等
D.斜边和一锐角对应相等
3.如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=( )
A.28° B.59° C.60° D.62°
4.如图,要用“HL”判定Rt△ABC和Rt△A′B′C′全等的条件是( )
A.AC=A′C′,BC=B′C′ B.∠A=∠A′,AB=A′B′
C.AC=A′C′,AB=A′B′ D.∠B=∠B′,BC=B′C′
5.在如图中,AB=AC,BE⊥AC于E,CF⊥AB于F,BE、CF交于点D,则下列结论中不正确的是( )
A.△ABE≌△ACF B.点D在∠BAC的平分线上
C.△BDF≌△CDE D.点D是BE的中点
6.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.75°
7.如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是( )
A.1 B.2 C.3 D.4
8.如图,AD=BC,∠C=∠D=90°,下列结论中不成立的是( )
A.∠DAE=∠CBE B.CE=DE
C.△DAE与△CBE不一定全等 D.∠1=∠2
9.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于( )
A.15 B.12 C.10 D.14
10.如图,在△ABC中,∠ACB的外角平分线与∠ABC的外角平分线相交于点D.则下列结论正确的是( )
A.AD平分BC B.AD平分∠CAB C.AD平分∠CDB D.AD⊥BC
11.如图,四边形ABCD中,∠A=90°,AD=2,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是( )
A.1 B.1.5 C.2 D.2.5
12.如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于E,PF⊥OD于F,下列结论:(1)PE=PF;(2)点P在∠COD的平分线上;(3)∠APB=90°﹣∠O,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二.填空题
13.如图,Rt△ABC和Rt△EDF中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条件 ,使Rt△ABC和Rt△EDF全等.
14.如图,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,∠A=50°,则∠DFE= .
15.在锐角△ABC中,有一点P它到B、C两点的距离相等,并且点P到AB、BC的距离也相等.∠A=50°,∠ACP=25°,则∠BPC= °.
16.如图,BE和CE分别为△ABC的内角∠ABC和外角∠ACD的平分线,BE⊥AC于点H,CF平分∠ACB交BE于点F,连接AE,则下列结论:①∠ECF=90°;②AE=CE;③∠BFC=90°+∠BAC;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的为 .
三.解答题
17.如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
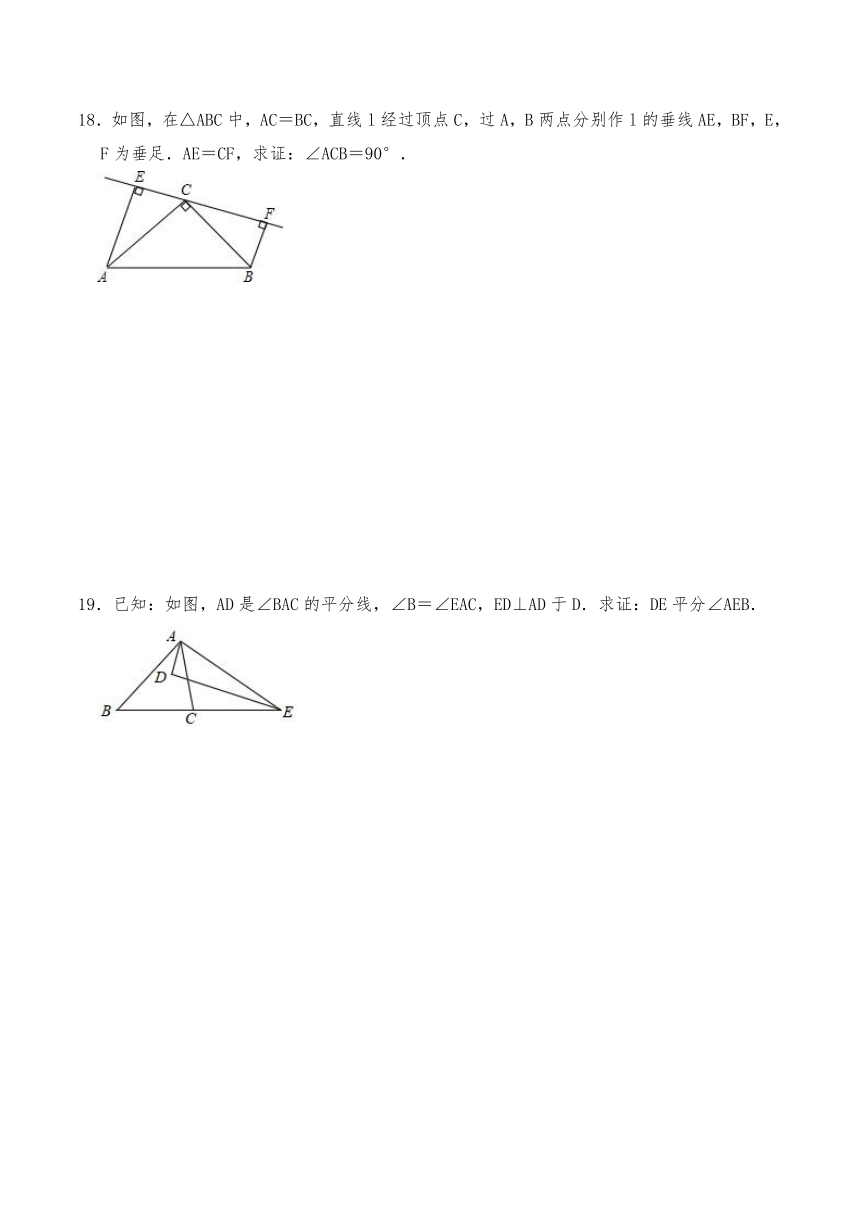
18.如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足.AE=CF,求证:∠ACB=90°.
19.已知:如图,AD是∠BAC的平分线,∠B=∠EAC,ED⊥AD于D.求证:DE平分∠AEB.
20.如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:EB=FC.
21.如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
22.数学课上,老师给出了如下问题:
已知:如图1,在Rt△ABC中,∠C=90°,AC=BC,延长CB到点D,∠DBE=45°,点F是边BC上一点,连结AF,作FE⊥AF,交BE于点 E.
(1)求证:∠CAF=∠DFE;
(2)求证:AF=EF.
经过独立思考后,老师让同学们小组交流.小辉同学说出了对于第二问的想法:“我想通过构造含有边AF和EF的全等三角形,因此我过点E作EG⊥CD于G(如图2所示),如果能证明Rt△ACF和Rt△FGE全等,问题就解决了.但是这两个三角形证不出来相等的边,好像这样作辅助线行不通.”小亮同学说:“既然这样作辅助线证不出来,再考虑有没有其他添加辅助线的方法.”请你顺着小亮同学的思路在图3中继续尝试,并完成(1)、(2)问的证明.
答案
一.选择题
B.B.B.C.D.B.C.C.B.B.C.C.
二.填空题
13.AB=ED.
14.40°.
15.110°.
16.①②③④⑤.
三.解答题
17.证明:(1)在△ABC和△DCB中,∠A=∠D=90°
AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形
∵Rt△ABC≌Rt△DCB
∴∠ACB=∠DCB
∴OB=OC
∴△OBC是等腰三角形
18.证明:如图,在Rt△ACE和Rt△CBF中,
,
∴Rt△ACE≌Rt△CBF(HL),
∴∠EAC=∠BCF,
∵∠EAC+∠ACE=90°,
∴∠ACE+∠BCF=90°,
∴∠ACB=180°﹣90°=90°.
19.证明:延长AD交BC于F,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵∠DFE=∠B+∠BAD,∠DAE=∠EAC+∠CAD,
∵∠B=∠EAC,
∴∠DFE=∠DAE,
∴AE=FE,
∵ED⊥AD,
∴ED平分∠AEB.
20.证明:∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DE=DF;
∵DE⊥AB于E,DF⊥AC于F.
∴在Rt△DBE和Rt△DCF中
∴Rt△DBE≌Rt△DCF(HL);
∴EB=FC.
21.解:根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=10;
②当P运动到与C点重合时,AP=AC,不合题意.
综上所述,当点P运动到距离点A为10时,△ABC与△APQ全等.
22.证明:(1)∵∠C=90°,
∴∠CAF+∠AFC=90°.
∵FE⊥AF,
∴∠DFE+∠AFC=90°.
∴∠CAF=∠DFE.
(2)如图3,在AC 上截取AG=BF,连结FG,
∵AC=BC,
∴AC﹣AG=BC﹣BF,即 CG=CF.
∵∠C=90°,
∴∠CGF=∠CFG=45°.
∴∠AGF=180°﹣∠CGF=135°.
∵∠DBE=45°,
∴∠FBE=180°﹣∠DBE=135°.
∴∠AGF=∠FBE.
由(1)可得:∠CAF=∠DFE.
∴△AGF≌△FBE(ASA).
∴AF=EF.
一.选择题
1.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.∠BAC=∠BAD B.AC=AD
C.∠ABC=∠ABD D.以上都不正确
2.下列判定直角三角形全等的方法,不正确的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.斜边和一直角边对应相等
D.斜边和一锐角对应相等
3.如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=( )
A.28° B.59° C.60° D.62°
4.如图,要用“HL”判定Rt△ABC和Rt△A′B′C′全等的条件是( )
A.AC=A′C′,BC=B′C′ B.∠A=∠A′,AB=A′B′
C.AC=A′C′,AB=A′B′ D.∠B=∠B′,BC=B′C′
5.在如图中,AB=AC,BE⊥AC于E,CF⊥AB于F,BE、CF交于点D,则下列结论中不正确的是( )
A.△ABE≌△ACF B.点D在∠BAC的平分线上
C.△BDF≌△CDE D.点D是BE的中点
6.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.75°
7.如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O.如果AB=AC,那么图中全等的直角三角形的对数是( )
A.1 B.2 C.3 D.4
8.如图,AD=BC,∠C=∠D=90°,下列结论中不成立的是( )
A.∠DAE=∠CBE B.CE=DE
C.△DAE与△CBE不一定全等 D.∠1=∠2
9.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于( )
A.15 B.12 C.10 D.14
10.如图,在△ABC中,∠ACB的外角平分线与∠ABC的外角平分线相交于点D.则下列结论正确的是( )
A.AD平分BC B.AD平分∠CAB C.AD平分∠CDB D.AD⊥BC
11.如图,四边形ABCD中,∠A=90°,AD=2,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是( )
A.1 B.1.5 C.2 D.2.5
12.如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于E,PF⊥OD于F,下列结论:(1)PE=PF;(2)点P在∠COD的平分线上;(3)∠APB=90°﹣∠O,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二.填空题
13.如图,Rt△ABC和Rt△EDF中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条件 ,使Rt△ABC和Rt△EDF全等.
14.如图,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,∠A=50°,则∠DFE= .
15.在锐角△ABC中,有一点P它到B、C两点的距离相等,并且点P到AB、BC的距离也相等.∠A=50°,∠ACP=25°,则∠BPC= °.
16.如图,BE和CE分别为△ABC的内角∠ABC和外角∠ACD的平分线,BE⊥AC于点H,CF平分∠ACB交BE于点F,连接AE,则下列结论:①∠ECF=90°;②AE=CE;③∠BFC=90°+∠BAC;④∠BAC=2∠BEC;⑤∠AEH=∠BCF,正确的为 .
三.解答题
17.如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
(1)求证:△ABC≌△DCB;
(2)△OBC是何种三角形?证明你的结论.
18.如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足.AE=CF,求证:∠ACB=90°.
19.已知:如图,AD是∠BAC的平分线,∠B=∠EAC,ED⊥AD于D.求证:DE平分∠AEB.
20.如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:EB=FC.
21.如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
22.数学课上,老师给出了如下问题:
已知:如图1,在Rt△ABC中,∠C=90°,AC=BC,延长CB到点D,∠DBE=45°,点F是边BC上一点,连结AF,作FE⊥AF,交BE于点 E.
(1)求证:∠CAF=∠DFE;
(2)求证:AF=EF.
经过独立思考后,老师让同学们小组交流.小辉同学说出了对于第二问的想法:“我想通过构造含有边AF和EF的全等三角形,因此我过点E作EG⊥CD于G(如图2所示),如果能证明Rt△ACF和Rt△FGE全等,问题就解决了.但是这两个三角形证不出来相等的边,好像这样作辅助线行不通.”小亮同学说:“既然这样作辅助线证不出来,再考虑有没有其他添加辅助线的方法.”请你顺着小亮同学的思路在图3中继续尝试,并完成(1)、(2)问的证明.
答案
一.选择题
B.B.B.C.D.B.C.C.B.B.C.C.
二.填空题
13.AB=ED.
14.40°.
15.110°.
16.①②③④⑤.
三.解答题
17.证明:(1)在△ABC和△DCB中,∠A=∠D=90°
AC=BD,BC为公共边,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形
∵Rt△ABC≌Rt△DCB
∴∠ACB=∠DCB
∴OB=OC
∴△OBC是等腰三角形
18.证明:如图,在Rt△ACE和Rt△CBF中,
,
∴Rt△ACE≌Rt△CBF(HL),
∴∠EAC=∠BCF,
∵∠EAC+∠ACE=90°,
∴∠ACE+∠BCF=90°,
∴∠ACB=180°﹣90°=90°.
19.证明:延长AD交BC于F,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵∠DFE=∠B+∠BAD,∠DAE=∠EAC+∠CAD,
∵∠B=∠EAC,
∴∠DFE=∠DAE,
∴AE=FE,
∵ED⊥AD,
∴ED平分∠AEB.
20.证明:∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DE=DF;
∵DE⊥AB于E,DF⊥AC于F.
∴在Rt△DBE和Rt△DCF中
∴Rt△DBE≌Rt△DCF(HL);
∴EB=FC.
21.解:根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=10;
②当P运动到与C点重合时,AP=AC,不合题意.
综上所述,当点P运动到距离点A为10时,△ABC与△APQ全等.
22.证明:(1)∵∠C=90°,
∴∠CAF+∠AFC=90°.
∵FE⊥AF,
∴∠DFE+∠AFC=90°.
∴∠CAF=∠DFE.
(2)如图3,在AC 上截取AG=BF,连结FG,
∵AC=BC,
∴AC﹣AG=BC﹣BF,即 CG=CF.
∵∠C=90°,
∴∠CGF=∠CFG=45°.
∴∠AGF=180°﹣∠CGF=135°.
∵∠DBE=45°,
∴∠FBE=180°﹣∠DBE=135°.
∴∠AGF=∠FBE.
由(1)可得:∠CAF=∠DFE.
∴△AGF≌△FBE(ASA).
∴AF=EF.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
