八年级数学上册试题 4.3坐标平面内的轴对称和平移-浙教版(含答案)
文档属性
| 名称 | 八年级数学上册试题 4.3坐标平面内的轴对称和平移-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 83.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 13:53:00 | ||
图片预览


文档简介
4.3坐标平面内的轴对称和平移
一.选择题
1.在平面直角坐标系中,将点(﹣2,3)先向右平移4个单位长度,再向下平移2个单位长度,得到的点的坐标为( )
A.(2,5) B.(﹣6,5) C.(2,1) D.(﹣6,1)
2.已知P(a,2)和Q(1,b)关于y轴对称,则(a+b)2021的值为( )
A.1 B.﹣1 C.32021 D.﹣32021
3.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都减去3,则所得图形与原图形的关系:将原图形( )
A.向上平移3个单位长度 B.向下平移3个单位长度
C.向左平移3个单位长度 D.向右平移3个单位长度
4.将点A(﹣2,3)通过以下哪种方式的平移,得到点A'(﹣5,7)( )
A.沿x轴向右平移3个单位长度,再沿y轴向上平移4个单位长度
B.沿x轴向左平移3个单位长度,再沿y轴向下平移4个单位长度
C.沿x轴向左平移4个单位长度,再沿y轴向上平移3个单位长度
D.沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度
5.在如图所示的单位正方形网格中,三角形ABC经过平移后得到三角形A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,则P1点的坐标为( )
A.(1.4,﹣1) B.(1.5,2) C.(﹣1.6,﹣1) D.(2.4,1)
6.已知点M(2,2),规定一次变换是:先作点M关于x轴对称,再将对称点向左平移1个单位长度,则连续经过2020次变换后,点M的坐标变为( )
A.(﹣2018,2) B.(﹣2018,﹣2) C.(﹣2017,2) D.(﹣2017,﹣2)
7.在平面直角坐标系中,若点M(﹣1,3)与点N(﹣1,a)之间的距离是5,那么a的值是( )
A.﹣2 B.8 C.2或8 D.﹣2或8
8.已知A(3,﹣2),B(1,0),把线段AB平移至线段CD,其中点A、B分别对应点C、D,若C(5,x),D(y,0),则x+y的值是( )
A.﹣1 B.0 C.1 D.2
9.已知A点坐标为(﹣4,5),将点A向右平移5个单位,再向下平移8个单位,得到点A1,再作点A1关于原点的对称点A2,则A2坐标为( )
A.(﹣1,3) B.(1,﹣3) C.(9,8) D.(﹣9,﹣8)
10.关于x的不等式组恰有5个整数解,且点A(a,3)不在坐标轴上,则A点关于x轴的对称点在第( )象限.
A.一、二 B.二、三 C.三、四 D.一、四
二.填空题
11.在平面直角坐标系中有一个对称图形,点A(3,2)与点B(3,﹣2)是此图形上的互为对称点,则在此图形上的另一点C(﹣1,﹣3)的对称点坐标为 .
12.若A(x,4)关于y轴的对称点是B(﹣3,y),则x= ,y= .点A关于x轴的对称点的坐标是 .
13.已知点A(m+2,﹣3)和点B(4,m﹣1),若直线AB∥x轴,则m的值为 .
14.在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),若将线段AB平移到A1B1,点A1,B1的坐标分别为(2,a),(b,3),则a2﹣2b的值为 .
15.已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,2),且|a﹣c|+=0,将线段PQ向右平移a个单位长度,其扫过的面积为24,那么a+b+c的值为 .
16.如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B(﹣1,2),第一次将矩形OABC绕右下角顶点O顺时针旋转90°得到矩形O1A1B1C1;第二次再将矩形O1A1B1C1绕右下角顶点C1顺时针旋转90°得到矩形O2A2B2C2,……按此规律,经过第五次旋转得到的点A5坐标为 .
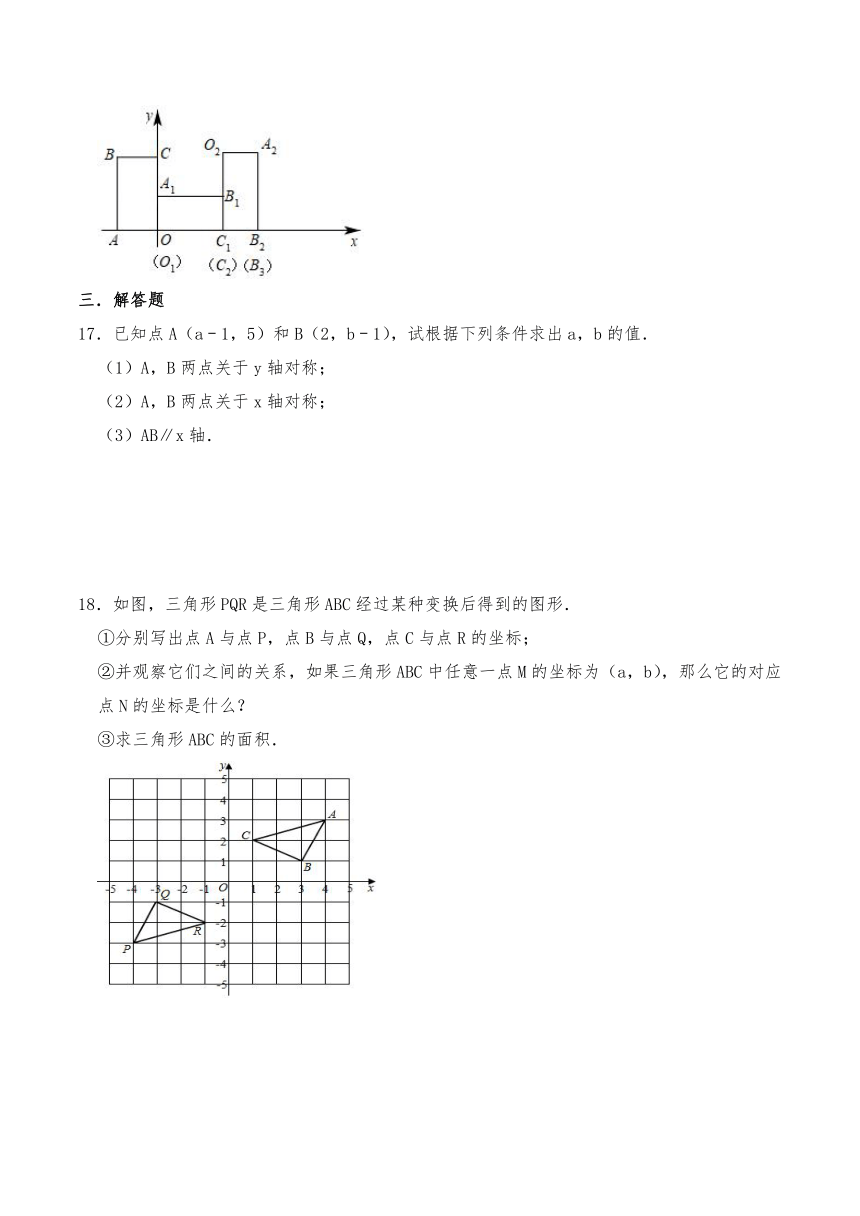
三.解答题
17.已知点A(a﹣1,5)和B(2,b﹣1),试根据下列条件求出a,b的值.
(1)A,B两点关于y轴对称;
(2)A,B两点关于x轴对称;
(3)AB∥x轴.
18.如图,三角形PQR是三角形ABC经过某种变换后得到的图形.
①分别写出点A与点P,点B与点Q,点C与点R的坐标;
②并观察它们之间的关系,如果三角形ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标是什么?
③求三角形ABC的面积.
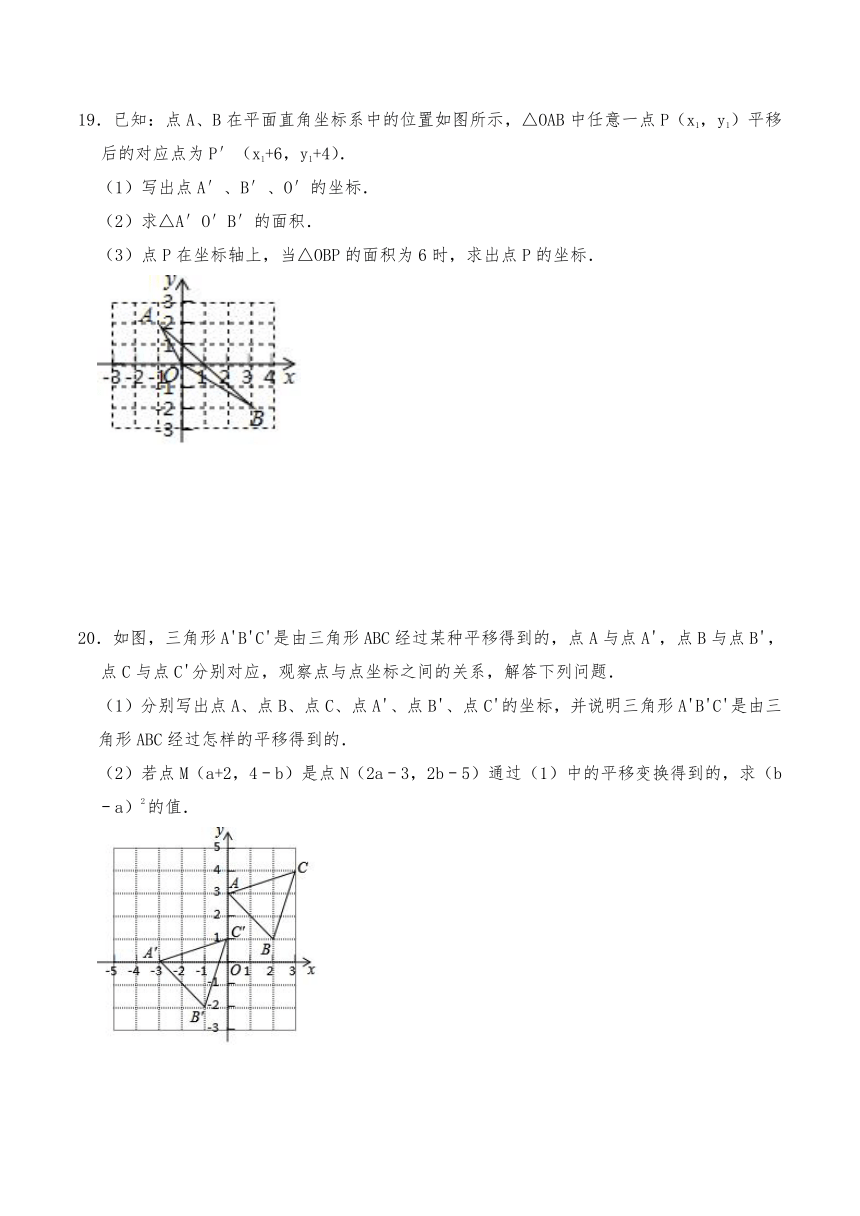
19.已知:点A、B在平面直角坐标系中的位置如图所示,△OAB中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)写出点A′、B′、O′的坐标.
(2)求△A′O′B′的面积.
(3)点P在坐标轴上,当△OBP的面积为6时,求出点P的坐标.
20.如图,三角形A'B'C'是由三角形ABC经过某种平移得到的,点A与点A',点B与点B',点C与点C'分别对应,观察点与点坐标之间的关系,解答下列问题.
(1)分别写出点A、点B、点C、点A'、点B'、点C'的坐标,并说明三角形A'B'C'是由三角形ABC经过怎样的平移得到的.
(2)若点M(a+2,4﹣b)是点N(2a﹣3,2b﹣5)通过(1)中的平移变换得到的,求(b﹣a)2的值.
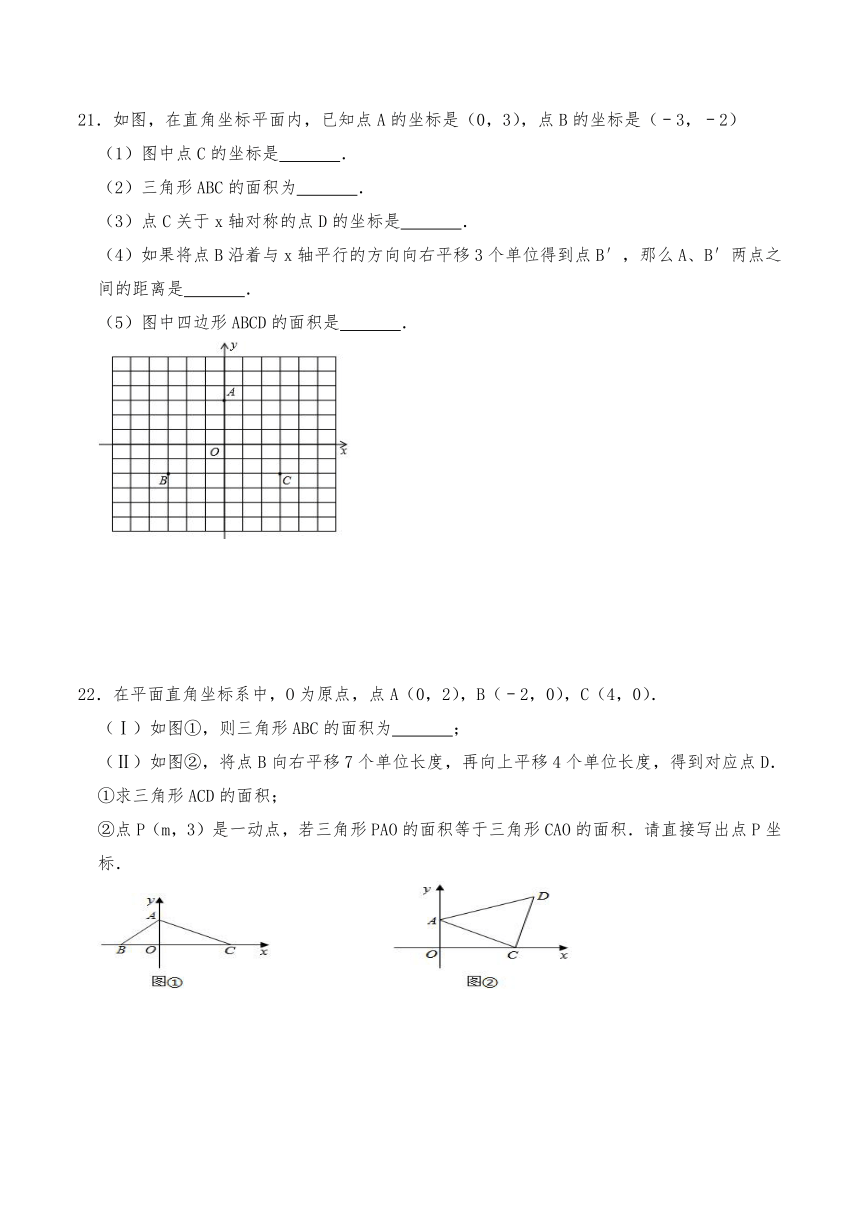
21.如图,在直角坐标平面内,已知点A的坐标是(0,3),点B的坐标是(﹣3,﹣2)
(1)图中点C的坐标是 .
(2)三角形ABC的面积为 .
(3)点C关于x轴对称的点D的坐标是 .
(4)如果将点B沿着与x轴平行的方向向右平移3个单位得到点B′,那么A、B′两点之间的距离是 .
(5)图中四边形ABCD的面积是 .
22.在平面直角坐标系中,O为原点,点A(0,2),B(﹣2,0),C(4,0).
(Ⅰ)如图①,则三角形ABC的面积为 ;
(Ⅱ)如图②,将点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D.
①求三角形ACD的面积;
②点P(m,3)是一动点,若三角形PAO的面积等于三角形CAO的面积.请直接写出点P坐标.
23.如图所示,BA⊥x轴于点A,点B的坐标为(﹣1,2),将线段BA沿x轴方向平移3个单位,平移后的线段为CD.
(1)点C的坐标为 ;线段BC与线段AD的位置关系是 .
(2)在四边形ABCD中,点P从点A出发,沿“AB→BC→CD”移动,移动到点D停止.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①直接写出点P在运动过程中的坐标(用含t的式子表示);
②当5秒<t<7秒时,四边形ABCP的面积为4,求点P的坐标.
答案
一.选择题
C.A.C.D.C.A.D.C.A.C.
二.填空题
11.(﹣1,3).
12.3;4;(3,﹣4).
13.﹣2.
14.﹣1.
15.18.
16.(9,2).
三.解答题
17.解:(1)A、B两点关于y轴对称,则
a﹣1=﹣2,b﹣1=5,
∴a=﹣1,b=6;
(2)A、B两点关于x轴对称,则
a﹣1=2,b﹣1=﹣5,
∴a=3,b=﹣4;
(3)AB∥x轴,则
b﹣1=5,a﹣1≠2,
∴b=6,a≠3.
18.解:①∵三角形PQR是三角形ABC经过某种变换后得到的图形,
∴点A(4,3)、点P(﹣4,﹣3),点B(3,1)、点Q(﹣3,﹣1),点C(1,2)、点R(﹣1,﹣2);
②观察三组对应点坐标可得:若三角形ABC中任意一点M的坐标为(a,b),
∴它的对应点N的坐标是(﹣a,﹣b);
③S△ABC=2×3﹣×1×2﹣×1×2﹣×3×1=.
19.解:(1)由题意A(﹣1,2),B(3,﹣2),
∴A′(5,6),B′(9,2),O′(6,4).
(2)S△A′O′B′=4×4﹣×1×2﹣×2×3﹣1×3﹣×4×4=2.
(3)当点P在x轴上时,P(6,0)或(﹣6,0).
当点P在y轴上时,P(0,4)或(0,﹣4).
20.解:(1)由图知,A(0,3),B(2,1),C(3,4),
A′(﹣3,0),B′(﹣1,﹣2),C′(0,1),
且△ABC向左平移3个单位,向下平移3个单位可以得到△A′B′C′;
(2)由(1)中的平移变换的2a﹣3﹣3=a+2,2b﹣5﹣3=4﹣b,
解得a=8,b=4,
则(b﹣a)2
=(4﹣8)2
=(﹣4)2
=16.
21.解:(1)根据题意得点C的坐标为(3,﹣2);
故答案为:(3,﹣2);
(2)△ABC的面积:.
故答案为:15;
(3)点C关于x轴对称的点D的坐标是(3,2);
故答案为:(3,2);
(4)将点B沿着与x轴平行的方向向右平移3个单位得到点B′(﹣3+3,﹣2),即(0,﹣2),
A、B′两点之间的距离是:3﹣(﹣2)=5;
故答案为:5;
(5),
∴四边形ABCD的面积为:S△ABC+S△ACD=15+6=21.
故答案为:21
22.解:(Ⅰ)∵A(0,2),B(﹣2,0),C(4,0),
∴OA=2,OB=2,OC=4,
∴S△ABC= BC AO=×6×2=6.
故答案为6.
(Ⅱ)①如图②中由题意D(5,4),连接OD.
S△ACD=S△AOD+S△COD﹣S△AOC
=×2×5+×4×4﹣×2×4=9.
②由题意:×2×|m|=×2×4,
解得m=±4,
∴P(﹣4,3)或(4,3).
23.解:(1)由题意知:C(﹣4,2),线段BC与线段AD的位置关系是平行.
故答案为(﹣4,2);平行.
(2)①当0≤t<2时,p(﹣1,t),
当2≤t≤5时,p(﹣t+1,2),
当5<t≤7时,p(﹣4,7﹣t);
②由题意知:AB=2,AD=3,PD=7﹣t,
∴s四边形ABCP=s四边形ABCD﹣s△ADP=4,
∴2×3﹣﹣×3×(7﹣t)=4,
解得t=,
∴7﹣t=7﹣=,
∴点P(﹣4,).
一.选择题
1.在平面直角坐标系中,将点(﹣2,3)先向右平移4个单位长度,再向下平移2个单位长度,得到的点的坐标为( )
A.(2,5) B.(﹣6,5) C.(2,1) D.(﹣6,1)
2.已知P(a,2)和Q(1,b)关于y轴对称,则(a+b)2021的值为( )
A.1 B.﹣1 C.32021 D.﹣32021
3.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都减去3,则所得图形与原图形的关系:将原图形( )
A.向上平移3个单位长度 B.向下平移3个单位长度
C.向左平移3个单位长度 D.向右平移3个单位长度
4.将点A(﹣2,3)通过以下哪种方式的平移,得到点A'(﹣5,7)( )
A.沿x轴向右平移3个单位长度,再沿y轴向上平移4个单位长度
B.沿x轴向左平移3个单位长度,再沿y轴向下平移4个单位长度
C.沿x轴向左平移4个单位长度,再沿y轴向上平移3个单位长度
D.沿x轴向左平移3个单位长度,再沿y轴向上平移4个单位长度
5.在如图所示的单位正方形网格中,三角形ABC经过平移后得到三角形A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,则P1点的坐标为( )
A.(1.4,﹣1) B.(1.5,2) C.(﹣1.6,﹣1) D.(2.4,1)
6.已知点M(2,2),规定一次变换是:先作点M关于x轴对称,再将对称点向左平移1个单位长度,则连续经过2020次变换后,点M的坐标变为( )
A.(﹣2018,2) B.(﹣2018,﹣2) C.(﹣2017,2) D.(﹣2017,﹣2)
7.在平面直角坐标系中,若点M(﹣1,3)与点N(﹣1,a)之间的距离是5,那么a的值是( )
A.﹣2 B.8 C.2或8 D.﹣2或8
8.已知A(3,﹣2),B(1,0),把线段AB平移至线段CD,其中点A、B分别对应点C、D,若C(5,x),D(y,0),则x+y的值是( )
A.﹣1 B.0 C.1 D.2
9.已知A点坐标为(﹣4,5),将点A向右平移5个单位,再向下平移8个单位,得到点A1,再作点A1关于原点的对称点A2,则A2坐标为( )
A.(﹣1,3) B.(1,﹣3) C.(9,8) D.(﹣9,﹣8)
10.关于x的不等式组恰有5个整数解,且点A(a,3)不在坐标轴上,则A点关于x轴的对称点在第( )象限.
A.一、二 B.二、三 C.三、四 D.一、四
二.填空题
11.在平面直角坐标系中有一个对称图形,点A(3,2)与点B(3,﹣2)是此图形上的互为对称点,则在此图形上的另一点C(﹣1,﹣3)的对称点坐标为 .
12.若A(x,4)关于y轴的对称点是B(﹣3,y),则x= ,y= .点A关于x轴的对称点的坐标是 .
13.已知点A(m+2,﹣3)和点B(4,m﹣1),若直线AB∥x轴,则m的值为 .
14.在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),若将线段AB平移到A1B1,点A1,B1的坐标分别为(2,a),(b,3),则a2﹣2b的值为 .
15.已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,2),且|a﹣c|+=0,将线段PQ向右平移a个单位长度,其扫过的面积为24,那么a+b+c的值为 .
16.如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B(﹣1,2),第一次将矩形OABC绕右下角顶点O顺时针旋转90°得到矩形O1A1B1C1;第二次再将矩形O1A1B1C1绕右下角顶点C1顺时针旋转90°得到矩形O2A2B2C2,……按此规律,经过第五次旋转得到的点A5坐标为 .
三.解答题
17.已知点A(a﹣1,5)和B(2,b﹣1),试根据下列条件求出a,b的值.
(1)A,B两点关于y轴对称;
(2)A,B两点关于x轴对称;
(3)AB∥x轴.
18.如图,三角形PQR是三角形ABC经过某种变换后得到的图形.
①分别写出点A与点P,点B与点Q,点C与点R的坐标;
②并观察它们之间的关系,如果三角形ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标是什么?
③求三角形ABC的面积.
19.已知:点A、B在平面直角坐标系中的位置如图所示,△OAB中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)写出点A′、B′、O′的坐标.
(2)求△A′O′B′的面积.
(3)点P在坐标轴上,当△OBP的面积为6时,求出点P的坐标.
20.如图,三角形A'B'C'是由三角形ABC经过某种平移得到的,点A与点A',点B与点B',点C与点C'分别对应,观察点与点坐标之间的关系,解答下列问题.
(1)分别写出点A、点B、点C、点A'、点B'、点C'的坐标,并说明三角形A'B'C'是由三角形ABC经过怎样的平移得到的.
(2)若点M(a+2,4﹣b)是点N(2a﹣3,2b﹣5)通过(1)中的平移变换得到的,求(b﹣a)2的值.
21.如图,在直角坐标平面内,已知点A的坐标是(0,3),点B的坐标是(﹣3,﹣2)
(1)图中点C的坐标是 .
(2)三角形ABC的面积为 .
(3)点C关于x轴对称的点D的坐标是 .
(4)如果将点B沿着与x轴平行的方向向右平移3个单位得到点B′,那么A、B′两点之间的距离是 .
(5)图中四边形ABCD的面积是 .
22.在平面直角坐标系中,O为原点,点A(0,2),B(﹣2,0),C(4,0).
(Ⅰ)如图①,则三角形ABC的面积为 ;
(Ⅱ)如图②,将点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D.
①求三角形ACD的面积;
②点P(m,3)是一动点,若三角形PAO的面积等于三角形CAO的面积.请直接写出点P坐标.
23.如图所示,BA⊥x轴于点A,点B的坐标为(﹣1,2),将线段BA沿x轴方向平移3个单位,平移后的线段为CD.
(1)点C的坐标为 ;线段BC与线段AD的位置关系是 .
(2)在四边形ABCD中,点P从点A出发,沿“AB→BC→CD”移动,移动到点D停止.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①直接写出点P在运动过程中的坐标(用含t的式子表示);
②当5秒<t<7秒时,四边形ABCP的面积为4,求点P的坐标.
答案
一.选择题
C.A.C.D.C.A.D.C.A.C.
二.填空题
11.(﹣1,3).
12.3;4;(3,﹣4).
13.﹣2.
14.﹣1.
15.18.
16.(9,2).
三.解答题
17.解:(1)A、B两点关于y轴对称,则
a﹣1=﹣2,b﹣1=5,
∴a=﹣1,b=6;
(2)A、B两点关于x轴对称,则
a﹣1=2,b﹣1=﹣5,
∴a=3,b=﹣4;
(3)AB∥x轴,则
b﹣1=5,a﹣1≠2,
∴b=6,a≠3.
18.解:①∵三角形PQR是三角形ABC经过某种变换后得到的图形,
∴点A(4,3)、点P(﹣4,﹣3),点B(3,1)、点Q(﹣3,﹣1),点C(1,2)、点R(﹣1,﹣2);
②观察三组对应点坐标可得:若三角形ABC中任意一点M的坐标为(a,b),
∴它的对应点N的坐标是(﹣a,﹣b);
③S△ABC=2×3﹣×1×2﹣×1×2﹣×3×1=.
19.解:(1)由题意A(﹣1,2),B(3,﹣2),
∴A′(5,6),B′(9,2),O′(6,4).
(2)S△A′O′B′=4×4﹣×1×2﹣×2×3﹣1×3﹣×4×4=2.
(3)当点P在x轴上时,P(6,0)或(﹣6,0).
当点P在y轴上时,P(0,4)或(0,﹣4).
20.解:(1)由图知,A(0,3),B(2,1),C(3,4),
A′(﹣3,0),B′(﹣1,﹣2),C′(0,1),
且△ABC向左平移3个单位,向下平移3个单位可以得到△A′B′C′;
(2)由(1)中的平移变换的2a﹣3﹣3=a+2,2b﹣5﹣3=4﹣b,
解得a=8,b=4,
则(b﹣a)2
=(4﹣8)2
=(﹣4)2
=16.
21.解:(1)根据题意得点C的坐标为(3,﹣2);
故答案为:(3,﹣2);
(2)△ABC的面积:.
故答案为:15;
(3)点C关于x轴对称的点D的坐标是(3,2);
故答案为:(3,2);
(4)将点B沿着与x轴平行的方向向右平移3个单位得到点B′(﹣3+3,﹣2),即(0,﹣2),
A、B′两点之间的距离是:3﹣(﹣2)=5;
故答案为:5;
(5),
∴四边形ABCD的面积为:S△ABC+S△ACD=15+6=21.
故答案为:21
22.解:(Ⅰ)∵A(0,2),B(﹣2,0),C(4,0),
∴OA=2,OB=2,OC=4,
∴S△ABC= BC AO=×6×2=6.
故答案为6.
(Ⅱ)①如图②中由题意D(5,4),连接OD.
S△ACD=S△AOD+S△COD﹣S△AOC
=×2×5+×4×4﹣×2×4=9.
②由题意:×2×|m|=×2×4,
解得m=±4,
∴P(﹣4,3)或(4,3).
23.解:(1)由题意知:C(﹣4,2),线段BC与线段AD的位置关系是平行.
故答案为(﹣4,2);平行.
(2)①当0≤t<2时,p(﹣1,t),
当2≤t≤5时,p(﹣t+1,2),
当5<t≤7时,p(﹣4,7﹣t);
②由题意知:AB=2,AD=3,PD=7﹣t,
∴s四边形ABCP=s四边形ABCD﹣s△ADP=4,
∴2×3﹣﹣×3×(7﹣t)=4,
解得t=,
∴7﹣t=7﹣=,
∴点P(﹣4,).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
