相似三角形复习1
图片预览


文档简介
课件21张PPT。相似三角形复习课引导者 陈积传1.相似三角形的定义:对应角相等、对应边成比例的三角形叫做相似三角形。2.相似比:相似三角形的对应边的比,叫做相似三角形的相似比。练习:一.相似三角形知识要点 △ABC∽△A/B/C/,如果BC=3,B/C/=1.5,那么△A/B/C/与
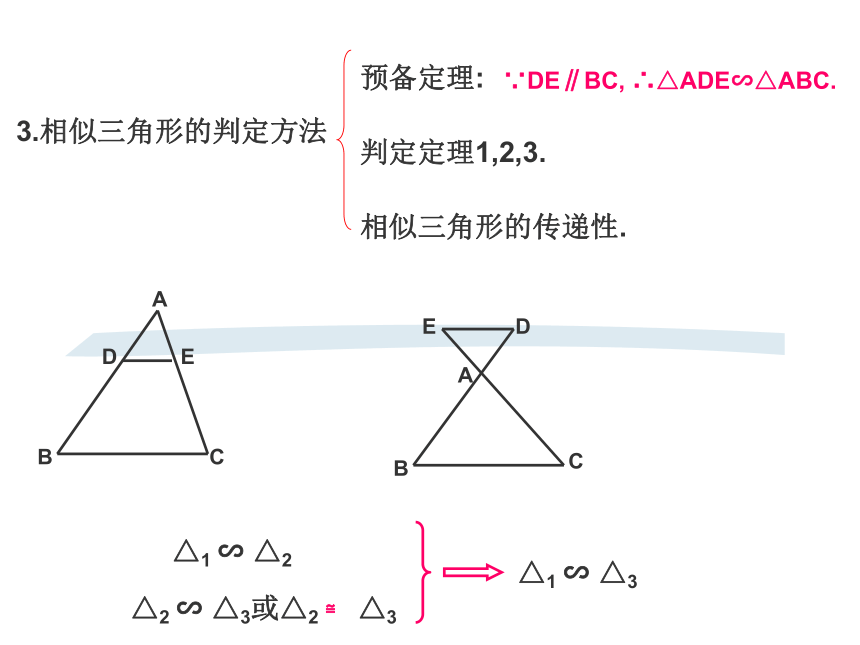
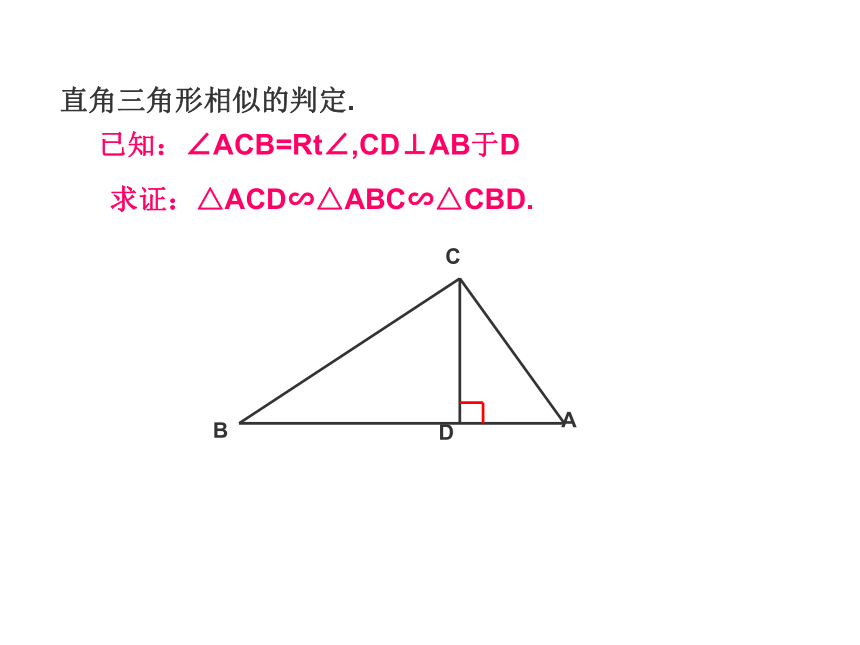
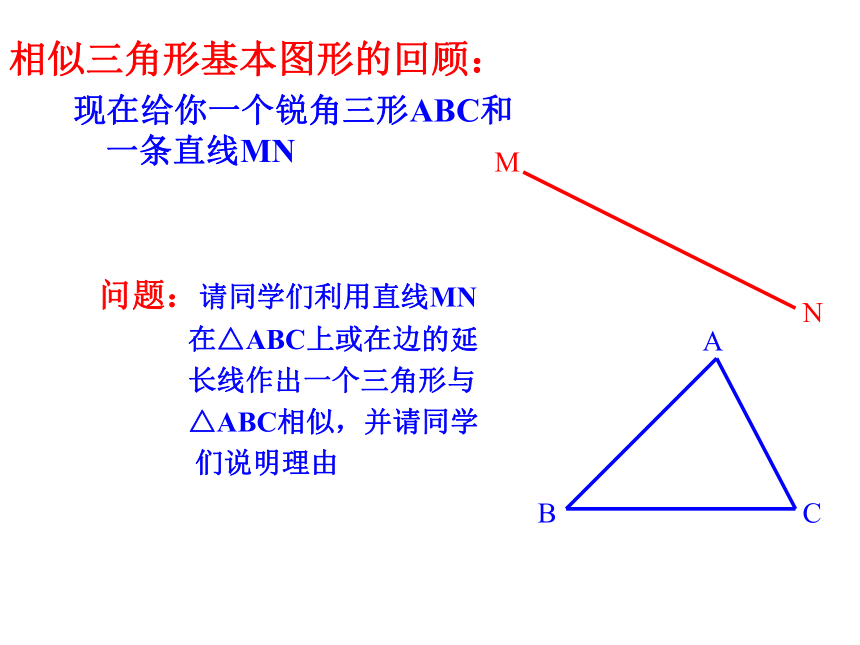
△ABC的相似比为_________.3.相似三角形的判定方法预备定理:相似三角形的传递性.判定定理1,2,3.△1 ∽ △2△2 ∽ △3或△2 ≌ △3△1 ∽ △3∵DE∥BC, ∴△ADE∽△ABC.直角三角形相似的判定.求证:△ACD∽△ABC∽△CBD.已知:∠ACB=Rt∠,CD⊥AB于D相似三角形基本图形的回顾:现在给你一个锐角三形ABC和一条直线MN
问题:请同学们利用直线MN
在△ABC上或在边的延
长线作出一个三角形与
△ABC相似,并请同学
们说明理由
ABCMN
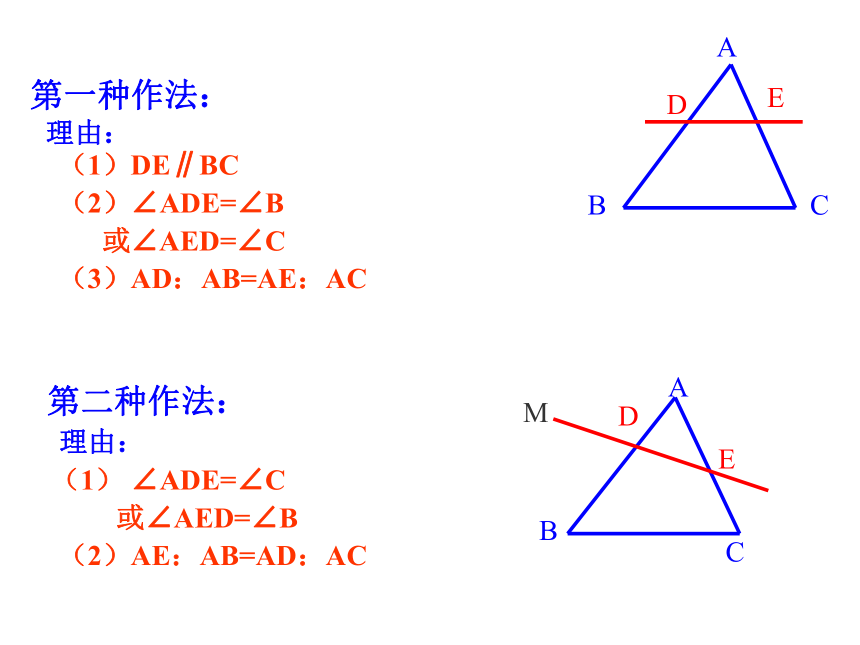
第一种作法:
理由:
(1)DE∥BC
(2)∠ADE=∠B
或∠AED=∠C
(3)AD:AB=AE:AC
第二种作法:
理由:
(1) ∠ADE=∠C
或∠AED=∠B
(2)AE:AB=AD:AC
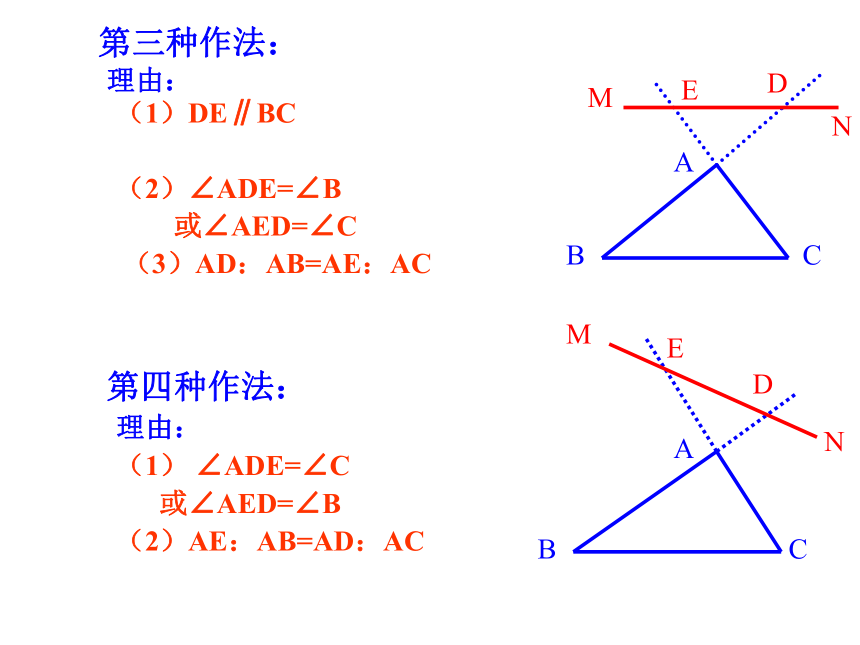
AEBCDADEBCM 第三种作法:
理由:
(1)DE∥BC
(2)∠ADE=∠B
或∠AED=∠C
(3)AD:AB=AE:AC
第四种作法:
理由:
(1) ∠ADE=∠C
或∠AED=∠B
(2)AE:AB=AD:AC
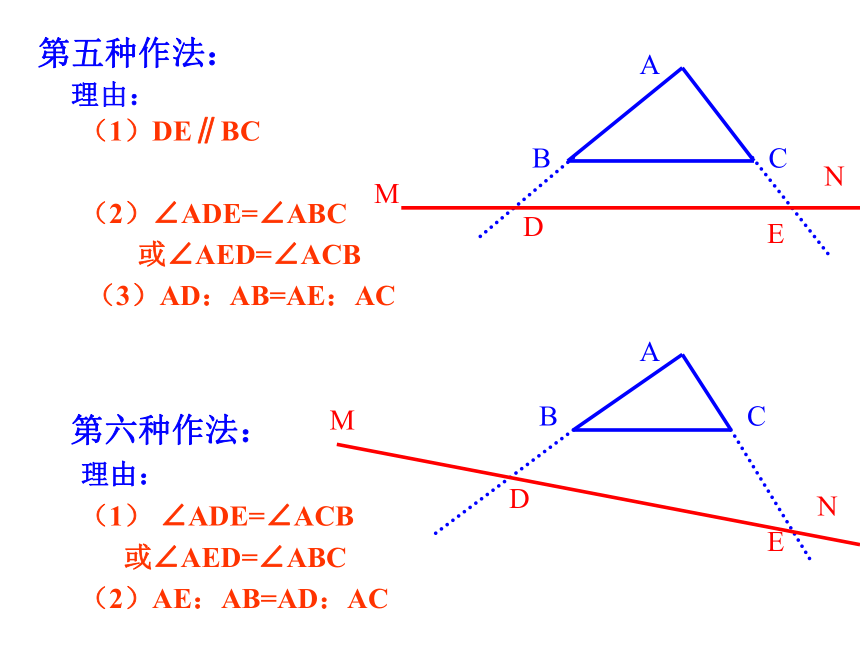
ABCEDABCEDMNMN第五种作法:
理由:
(1)DE∥BC
(2)∠ADE=∠ABC
或∠AED=∠ACB
(3)AD:AB=AE:AC
第六种作法:
理由:
(1) ∠ADE=∠ACB
或∠AED=∠ABC
(2)AE:AB=AD:AC
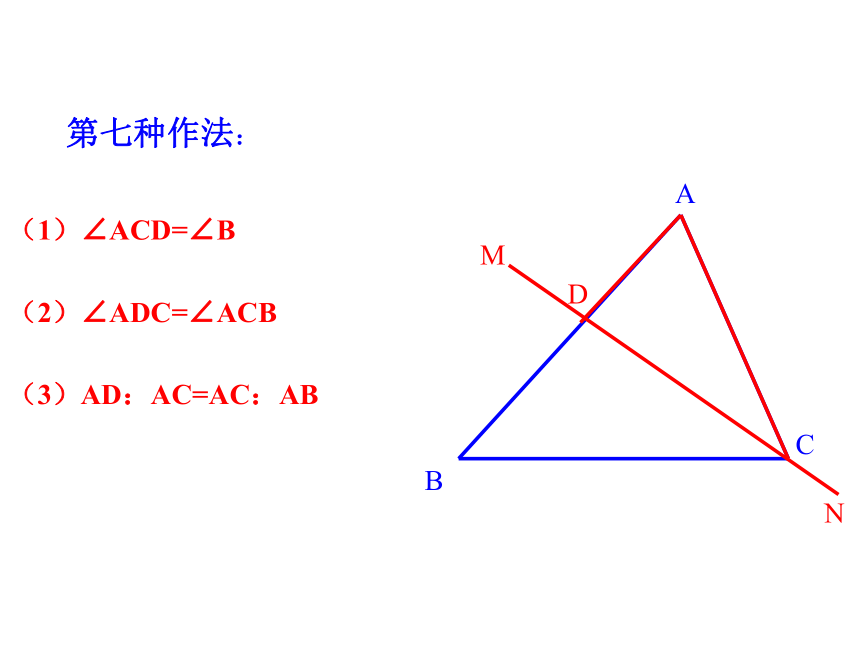
ABCABCDEMNMDEN 第七种作法:(1)∠ACD=∠B
(2)∠ADC=∠ACB
(3)AD:AC=AC:AB
ABD CMNADEBACBABCD△ADE绕点A旋转DCADEBCABCDEBCADE点E移到与C点重合∠ACB=Rt∠CD⊥AB相似三角形基本图形的回顾: 证明:∵CD⊥AB, E为AC的中点
∴ DE=AE
∴∠EDA=∠A
∵ ∠EDA=∠FDB
∴∠A=∠FDB
∵∠ACB= Rt ∠
∴ ∠A=∠FCD
∴ ∠FDB=∠FCD
∵ △FDB∽△FCD
∴ BD:CD=DF:CF
∴ BD·CF=CD·DF
例1 如图,CD是Rt△ABC斜边上的高,E为AC的中点,
ED交CB的延长线于F。CEADFB这个图形中有几个相似三角形的基本图形求证:BD·CF=CD·DF二.知识应用:1.找一找:(1) 如图1,已知:DE∥BC,EF ∥AB,则图中共有_____对三角形相似.(2) 如图2,已知:△ABC中, ∠ACB=Rt∠ ,CD⊥ AB于D,DE⊥BC于E,则图中共有_____个三角形和△ABC相似.34(4)已知:四边形ABCD内接于⊙O,连结AC和BD交于点E,则图中共有_____对三角形相似.2(3)如图3,∠1= ∠2= ∠3,则图中相似三角形的组数为
________.4 1.如图,P是△ABC中AB边上的一点,要使△ACP和△ABC相似,则需添加一个条件:_____________________________________
。 ∠ACP=∠B;或∠APC=∠ACB;或AP:AC=AC:AB即AC2=AP·AB2.做一做:2.已知,如图,梯形ABCD中,AD∥BC, ∠A=900,对角线BD⊥CD求证:
(1) △ABD∽△DCB;
(2)BD2=AD·BC如图,点C,D在线段AB上, △PCD是等边三角形.
(1)当AC,CD,DB满足什么关系时, △ACP∽ △PBD.
(2)当△ACP∽ △PBD时,求∠APB的度数.3.想一想:变式:如图,点C,D在线段AB上, △PCD是等边三角形, ∠APB=1200
(1)写出所有的相似三角形;
(2)若AC=4,BD=9,求CD的长4.练一练:1.将两块完全相同的等腰直角三角形摆放成如图所示的样子,假设图形中的所有点,线都在同一平面内,共有几对相似三角形______________.GABCDEF1232.如图,正方形ABCD的边长为8,E是AB的中点,点M,N分别在BC,CD上,且CM=2,则当CN=_________时,△CMN与△ADE的形状相同。3.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O,B,P为顶点的三角形与△ABC相似,则点P的坐标是__________________.·P.如图, △ABC中,AB=6,BC=4,AC=3,点P在BC上运动,过P点作∠DPB=∠A,PD交AB于D,设PB=x,AD=y.
(1)求y关于x的函数关系式和x的取值范围.
(2)当x取何值时,y最小,最小值是多少?6.思考题:
△ABC的相似比为_________.3.相似三角形的判定方法预备定理:相似三角形的传递性.判定定理1,2,3.△1 ∽ △2△2 ∽ △3或△2 ≌ △3△1 ∽ △3∵DE∥BC, ∴△ADE∽△ABC.直角三角形相似的判定.求证:△ACD∽△ABC∽△CBD.已知:∠ACB=Rt∠,CD⊥AB于D相似三角形基本图形的回顾:现在给你一个锐角三形ABC和一条直线MN
问题:请同学们利用直线MN
在△ABC上或在边的延
长线作出一个三角形与
△ABC相似,并请同学
们说明理由
ABCMN
第一种作法:
理由:
(1)DE∥BC
(2)∠ADE=∠B
或∠AED=∠C
(3)AD:AB=AE:AC
第二种作法:
理由:
(1) ∠ADE=∠C
或∠AED=∠B
(2)AE:AB=AD:AC
AEBCDADEBCM 第三种作法:
理由:
(1)DE∥BC
(2)∠ADE=∠B
或∠AED=∠C
(3)AD:AB=AE:AC
第四种作法:
理由:
(1) ∠ADE=∠C
或∠AED=∠B
(2)AE:AB=AD:AC
ABCEDABCEDMNMN第五种作法:
理由:
(1)DE∥BC
(2)∠ADE=∠ABC
或∠AED=∠ACB
(3)AD:AB=AE:AC
第六种作法:
理由:
(1) ∠ADE=∠ACB
或∠AED=∠ABC
(2)AE:AB=AD:AC
ABCABCDEMNMDEN 第七种作法:(1)∠ACD=∠B
(2)∠ADC=∠ACB
(3)AD:AC=AC:AB
ABD CMNADEBACBABCD△ADE绕点A旋转DCADEBCABCDEBCADE点E移到与C点重合∠ACB=Rt∠CD⊥AB相似三角形基本图形的回顾: 证明:∵CD⊥AB, E为AC的中点
∴ DE=AE
∴∠EDA=∠A
∵ ∠EDA=∠FDB
∴∠A=∠FDB
∵∠ACB= Rt ∠
∴ ∠A=∠FCD
∴ ∠FDB=∠FCD
∵ △FDB∽△FCD
∴ BD:CD=DF:CF
∴ BD·CF=CD·DF
例1 如图,CD是Rt△ABC斜边上的高,E为AC的中点,
ED交CB的延长线于F。CEADFB这个图形中有几个相似三角形的基本图形求证:BD·CF=CD·DF二.知识应用:1.找一找:(1) 如图1,已知:DE∥BC,EF ∥AB,则图中共有_____对三角形相似.(2) 如图2,已知:△ABC中, ∠ACB=Rt∠ ,CD⊥ AB于D,DE⊥BC于E,则图中共有_____个三角形和△ABC相似.34(4)已知:四边形ABCD内接于⊙O,连结AC和BD交于点E,则图中共有_____对三角形相似.2(3)如图3,∠1= ∠2= ∠3,则图中相似三角形的组数为
________.4 1.如图,P是△ABC中AB边上的一点,要使△ACP和△ABC相似,则需添加一个条件:_____________________________________
。 ∠ACP=∠B;或∠APC=∠ACB;或AP:AC=AC:AB即AC2=AP·AB2.做一做:2.已知,如图,梯形ABCD中,AD∥BC, ∠A=900,对角线BD⊥CD求证:
(1) △ABD∽△DCB;
(2)BD2=AD·BC如图,点C,D在线段AB上, △PCD是等边三角形.
(1)当AC,CD,DB满足什么关系时, △ACP∽ △PBD.
(2)当△ACP∽ △PBD时,求∠APB的度数.3.想一想:变式:如图,点C,D在线段AB上, △PCD是等边三角形, ∠APB=1200
(1)写出所有的相似三角形;
(2)若AC=4,BD=9,求CD的长4.练一练:1.将两块完全相同的等腰直角三角形摆放成如图所示的样子,假设图形中的所有点,线都在同一平面内,共有几对相似三角形______________.GABCDEF1232.如图,正方形ABCD的边长为8,E是AB的中点,点M,N分别在BC,CD上,且CM=2,则当CN=_________时,△CMN与△ADE的形状相同。3.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O,B,P为顶点的三角形与△ABC相似,则点P的坐标是__________________.·P.如图, △ABC中,AB=6,BC=4,AC=3,点P在BC上运动,过P点作∠DPB=∠A,PD交AB于D,设PB=x,AD=y.
(1)求y关于x的函数关系式和x的取值范围.
(2)当x取何值时,y最小,最小值是多少?6.思考题:
同课章节目录
