7.1常量与变量

课件27张PPT。一、情境小屋 同学们到过江西吗？你知道江西九江到嘉兴有多远吗？如果你不知道，那么解答下面一道简单的数学题就知道啦！
谌老师从九江一路而来，到嘉兴城区用了１０小时３０分钟，谌老师的车速平均约为80千米/时，请大家说说，江西九江到嘉兴有多少千米？（千米）现在提出一个假设：由上可知，九江到嘉兴路程约为840千米，（1）如果老师必须在10小时赶到，问车速是多少？
（2）如果老师9.5小时中赶到，问车速又是多少？９小时、8.5小时……呢？ 容易求出（1） （ 千米/时）（ 千米/时）（2）………………………… s、,v、,t三个量中，s相对不变，而v、,t相对可变，并存在依赖关系。即速度v随时间t的变化而变化。 7.1常量与变量二、互动乐园
1.课前热身
（1)当x=-1，0，1.5，3时，求代数式3x-2的值；
（2）已知二元一次方程2x-y=1,请写出满足方程的若干组解。

由此，在代数式和方程中，你发现了什么？
（1）中代数式值与x相互依存，
（2）中x,y相互依存,并且两个始终处于变化之中。
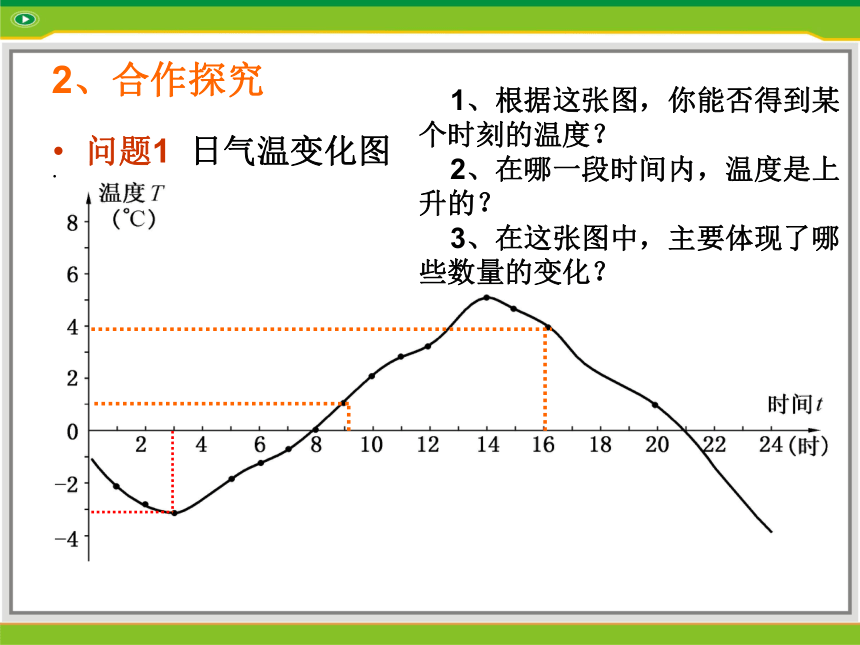
2、合作探究问题1 日气温变化图
1、根据这张图，你能否得到某个时刻的温度？
2、在哪一段时间内，温度是上升的？
3、在这张图中，主要体现了哪些数量的变化？探究结论1：
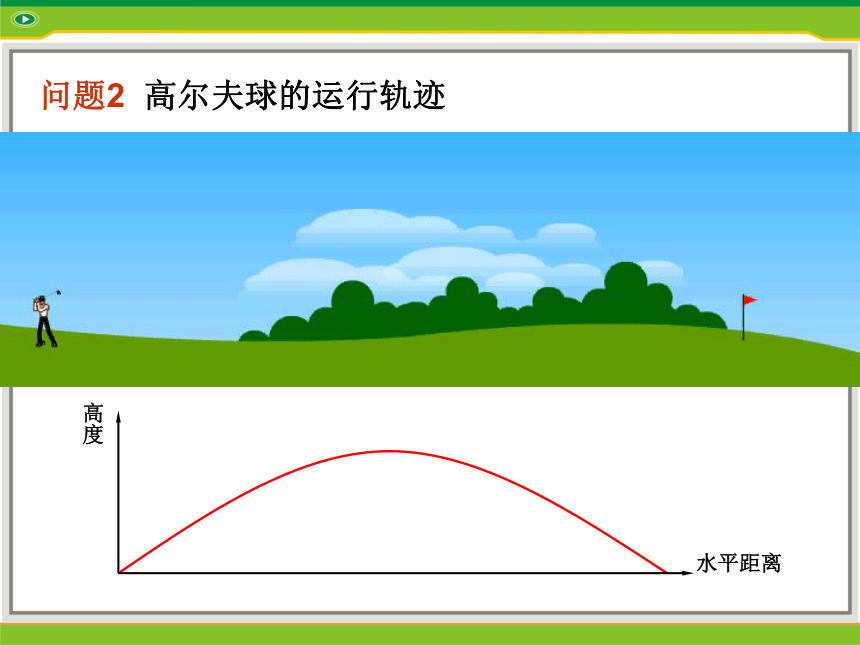
从图中我们可以看到，随着时间t（时）的变化，相应地气温T（℃）也随之变化．问题2 高尔夫球的运行轨迹 高度水平距离探究结论2： 随着水平距离l的变化，高度h也随之变化．每一个水平距离l都有惟一的高度h与之对应． 问题3 利率问题 银行对各种不同的存款方式都规定了相应的利率，下表是2002年7月中国工商银行为“整存整取”的存款方式规定的利率：
观察上表，说说其中哪些地方发生了变化？
探究结论3： 随着存期x的变化，年利率y都随之变化，每一个存期x的值都有惟一的利率的y值与之对应。 问题4 收音机频率问题 收音机上的刻度盘的波长和频率分别是用米（m）和千赫兹（kHz）为单位标刻的．下面是一些对应的数：

观察表格，你发现l与f之间存在怎样的规律？波长越大，频率f将会怎样变化？
在表格中的数据中，你还发现了什么？
l和f的乘积是一个定值，即lf=300000，或者写作
问题５ 水中的波纹把一块小石头投入池缸中，就会激起一阵阵的波纹
在这个图中，请同学留意：哪些是在不断变化的？（看演示图）
若设圆的半径为r，
那么
面积 S= πr2
周长 C=2πr
探究结论5： 面积S和周长Ｃ随着半径r的变化而变化．每一个半径r都有惟一的一个面积S、周长C与之对应．形成概念1、知识联结
（1）观察引例变化过程，有那些共同之处？
①一个变化过程；
②两个变量；
③一种对应，即一个量随另一个量的变化而变化。
（2）在
和　　　　中，30000是一个定值，π一个常数，在变化过程中它们变化吗？
l,f,S,r它们变化吗？
２、归纳定义 （1）在某一变化过程中，可以取不同数值的量，叫做变量。（如：S、r、f、l等）；
（2）反之，在某一变化过程中，取值保持不变的量，叫做常量。（如：常数、定值300000等）；
变量和常量是相对的。
？考考聪明人声音在空气中传播的速度v(m/s)与
温度t(oC)之间的关系式是v=331+0.6t
，其中常量是________，变量是_____。331,0.6v,t长方形的长和宽分别是a与b，
周长Ｃ＝2(a＋b)，其中常量是___,
变量是______。2a,b,Ｃ我国是一个严重缺水的国家，大家应倍加珍惜水资源，节约用水。若拧不紧的水龙头每秒钟会滴下2滴水，每滴水约0.05毫升。小明同学在洗手时，没有把水龙头拧紧，当小明离开x小时后水龙头滴了y毫升水.在这一变化过程中哪些量是变量？哪些量是常量？
小明到商店买练习簿，每本单价2元，
购买的总数x（本）与总金额y（元），
其中的常量是 变量是 。
2x,y我国“神舟七号”于北京时间 2008年９月28日17时37分，在内蒙古四子王旗成功着陆。 在着陆前的最后48分
时间内，它是在耐高温表层的保护下，以7800米/秒的
速度冲入100千米厚的地球大气层。 空气阻力的作用下，它在距地球表面10千米左右时，
以180米／秒的速度下降 ，此时直径20多米的降落伞
自动打开。 速度、飞船着陆前48分时的位置到着陆点的距离， 飞船所受地球的引力这些量 ， 哪些是常量？哪些是变量？题目思考：三、点金阁这节课，你有哪些收获？ 归纳小结：
1、两个概念： 常量与变量
2、一个注意：常量与变量是相对的。
四、沉思阁向自己挑战：
矩形ABCD中，当点P在边AD上从A向D移动时，有些线段的长度和三角形的面积始终保持不变，而有些则发生了变化。（1）试分别举出变化与不变化的两条线段与两个三角形。
（2）假设长方形的长AD为10cm，宽AB为4cm，线段AP的长为xcm，你能用x表示出△PCD的面积S吗?试试看!
解：（1）线段长度变化的线段是：PB，PC；不变化的线段，如BC，CD.
面积变化的三角形是：△PAB，△PCD；面积不变化的三角形是：△PBC.
（2）∵AD=10cm，AP=x cm
∴PD=（10-x）㎝
∵CD=AB=4cm，
∴S=CD·PD=4×（10-x）
=（20-2 x）（cm2）.在靠墙（墙的长度为18米）的地方围建一个长方形的养鸡场，另三边用竹篱笆围成，如果竹篱笆总长为35米，求养鸡场的长与宽有何关系，试求宽的范围？五、趣味大观你能预测自己将来的身高吗？若x，y分别表示父母的身高,h男，h女分别表示儿女成人
时的身高，则有关系式h男＝０.５４（x＋y ）；h女＝（０.９７５x＋y）÷２你们能预测出你成人时的身高吗？这里什么是
常量？什么是变量？