浙教版七年级数学上册试题 6.3线段的长短比较(含答案)
文档属性
| 名称 | 浙教版七年级数学上册试题 6.3线段的长短比较(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 70.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 02:11:24 | ||
图片预览



文档简介
6.3线段的长短比较
一.选择题
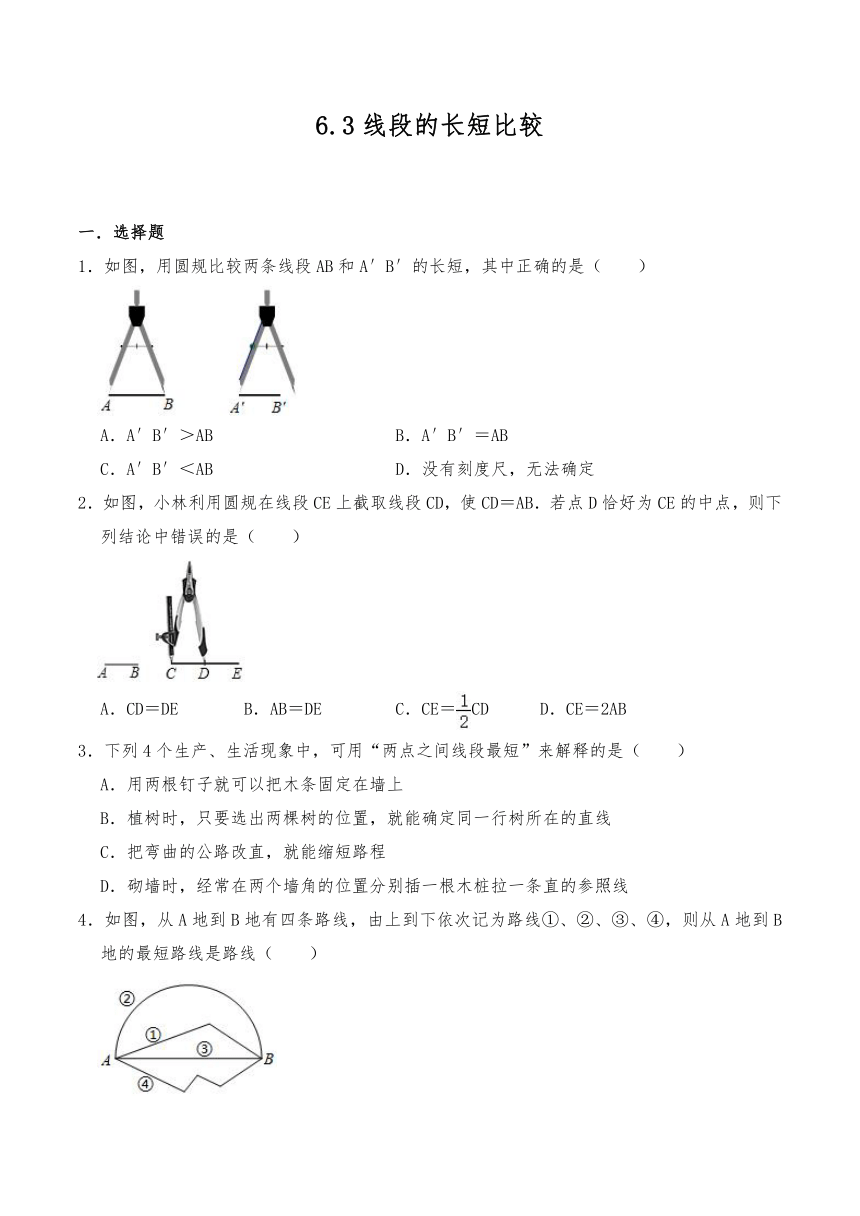
1.如图,用圆规比较两条线段AB和A′B′的长短,其中正确的是( )
A.A′B′>AB B.A′B′=AB
C.A′B′<AB D.没有刻度尺,无法确定
2.如图,小林利用圆规在线段CE上截取线段CD,使CD=AB.若点D恰好为CE的中点,则下列结论中错误的是( )
A.CD=DE B.AB=DE C.CE=CD D.CE=2AB
3.下列4个生产、生活现象中,可用“两点之间线段最短”来解释的是( )
A.用两根钉子就可以把木条固定在墙上
B.植树时,只要选出两棵树的位置,就能确定同一行树所在的直线
C.把弯曲的公路改直,就能缩短路程
D.砌墙时,经常在两个墙角的位置分别插一根木桩拉一条直的参照线
4.如图,从A地到B地有四条路线,由上到下依次记为路线①、②、③、④,则从A地到B地的最短路线是路线( )
A.① B.② C.③ D.④
5.已知点A,B,C为平面内三点,给出下列条件:①AC=BC;②AB=2BC;③AC=BC=AB.选择其中一个条件就能得到“点C是线段AB中点”的是( )
A.① B.③ C.①或③ D.①或②或③
6.已知线段AB=9,点C是AB的中点,点D是AB的三等分点,则C,D两点间距离为( )
A.3 B.1.5 C.1.2 D.1
7.如图,在公路MN两侧分别有A1,A2…A7,七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
①车站的位置设在C点好于B点;
②车站的位置设在B点与C点之间公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关;
④车站的位置设在BC段公路的最中间处要好于设在点B及点C处.
A.①③ B.③④ C.②③ D.②
二.填空题
8.如图,用圆规比较两条线段A'B'和AB的长短,则AB A'B'.(填“>”“=”或“<”)
9.如果点C在线段AB上,且点C不与点A、B重合,那么AB BC.(填“>”或“<”)
10.长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为 .
11.点A、B、C在直线l上,AB=4cm,BC=6cm,点E是AB中点,点F是BC的中点,EF= .
12.如图,长度为12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段MC的长度为 cm.
13.已知:线段AB=5cm,在直线AB上有一点C,并且BC=3cm,则AC= cm.
14.已知点C在直线AB上且BC=2AB,取AC的中点D,已知线段BD的长为6,则线段AB的长为 .
15.某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C,区有10人,三个区在一直线上,位置如图所示,公司的接送车打算在此间只设一个停靠点,为要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在 区.
16.下列有四个生活、生产现象:其中可用基本事实“两点之间,线段最短”来解释的现象有 (填序号).
①有两个钉子就可以把木条固定在墙上;
②A从地到B地架设电线,总是尽可能沿着线段AB架设;
③植树时,只要定出两棵树的位置,就能确定同一行所在的直线;
④把弯曲的公路改直,就能缩短路程,
三.解答题
17.如图所示,工厂A与工厂B想在公路m旁修建一座共用的仓库O,并且要求O到A与O到B的距离之和最短,请你在m上确定仓库应修建的O点位置,同时说明你选择该点的理由.
18.(南关区校级月考)请你判断下列两个生活情景所蕴含的数学道理.
情景一:如图,小明家到学校有3条路可走,一般情况下,小明通常走第二条路,其中的数学道理是 .
情景二:同学们做体操时,为了保证一队同学站成一条直线,先让两个同学站好不动,其他同学依次往后站,要求目视前方只能看到各自前面的那个同学,请你说明其中的道理: .
19.如图,线段AB=8cm,C是线段AB上一点,AC=3cm,M是AB的中点,N是AC的中点.
(1)求线段CM、NM的长;
(2)若线段AC=m,线段BC=n,求MN的长度(m<n用含m,n的代数式表示).
20.(1)如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点,求线段MN的长度;
(2)已知点C在线段BA的延长线上,点M,N分别是AC,BC的中点,设BC﹣AC=a,请根据题意画出图形并求MN的长度;
(3)在(1)的条件下,动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
答案
一.选择题
C.C.C.C.B.B.A.
二.填空题
8.<.
9.>.
10.8cm.
11.5cm或1cm.
12.2.
13.2cm或8.
14.4或12.
15.A.
16.②④.
三.解答题
17.解:如图,连接AB交直线m于点O,
则O点即为所求的点.
∴OA+OB最短.
18.解:情景一:如图,小明家到学校有3条路可走,一般情况下,小明通常走第二条路,其中的数学道理是两点之间线段最短;
故答案为:两点之间线段最短;
故答案为:两点确定一条直线.
19.解:(1)∵AB=8cm,M是AB的中点,
∴AM=AB=6cm,
∴CM=AM﹣AC=4﹣3=1(cm);
∴AM=AB=4cm,AN=AC=1.6cm,
(2)∵AC=m,BC=n,
∵M是AB的中点,N是AC的中点,
∴MN=AM﹣AN=(m+n)﹣m=n.
20.解:(1)∵线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点,
∴CM=AC=5厘米,CN=BC=3厘米,
(2)如图,∵点M,N分别是AC,BC的中点,
∴MN=CN﹣CM=(BC﹣AC)=a;
(3)①当0<t≤8时,C是线段PQ的中点,得
10﹣2t=6﹣t,解得t=4;
②当5<t≤时,P为线段CQ的中点,2t﹣10=16﹣3t,解得t=;
③当<t≤6时,Q为线段PC的中点,6﹣t=3t﹣16,解得t=;
④当3<t≤8时,C为线段PQ的中点,2t﹣10=t﹣6,解得t=4(舍),
综上所述:t=4或或.
一.选择题
1.如图,用圆规比较两条线段AB和A′B′的长短,其中正确的是( )
A.A′B′>AB B.A′B′=AB
C.A′B′<AB D.没有刻度尺,无法确定
2.如图,小林利用圆规在线段CE上截取线段CD,使CD=AB.若点D恰好为CE的中点,则下列结论中错误的是( )
A.CD=DE B.AB=DE C.CE=CD D.CE=2AB
3.下列4个生产、生活现象中,可用“两点之间线段最短”来解释的是( )
A.用两根钉子就可以把木条固定在墙上
B.植树时,只要选出两棵树的位置,就能确定同一行树所在的直线
C.把弯曲的公路改直,就能缩短路程
D.砌墙时,经常在两个墙角的位置分别插一根木桩拉一条直的参照线
4.如图,从A地到B地有四条路线,由上到下依次记为路线①、②、③、④,则从A地到B地的最短路线是路线( )
A.① B.② C.③ D.④
5.已知点A,B,C为平面内三点,给出下列条件:①AC=BC;②AB=2BC;③AC=BC=AB.选择其中一个条件就能得到“点C是线段AB中点”的是( )
A.① B.③ C.①或③ D.①或②或③
6.已知线段AB=9,点C是AB的中点,点D是AB的三等分点,则C,D两点间距离为( )
A.3 B.1.5 C.1.2 D.1
7.如图,在公路MN两侧分别有A1,A2…A7,七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
①车站的位置设在C点好于B点;
②车站的位置设在B点与C点之间公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关;
④车站的位置设在BC段公路的最中间处要好于设在点B及点C处.
A.①③ B.③④ C.②③ D.②
二.填空题
8.如图,用圆规比较两条线段A'B'和AB的长短,则AB A'B'.(填“>”“=”或“<”)
9.如果点C在线段AB上,且点C不与点A、B重合,那么AB BC.(填“>”或“<”)
10.长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为 .
11.点A、B、C在直线l上,AB=4cm,BC=6cm,点E是AB中点,点F是BC的中点,EF= .
12.如图,长度为12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段MC的长度为 cm.
13.已知:线段AB=5cm,在直线AB上有一点C,并且BC=3cm,则AC= cm.
14.已知点C在直线AB上且BC=2AB,取AC的中点D,已知线段BD的长为6,则线段AB的长为 .
15.某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C,区有10人,三个区在一直线上,位置如图所示,公司的接送车打算在此间只设一个停靠点,为要使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应在 区.
16.下列有四个生活、生产现象:其中可用基本事实“两点之间,线段最短”来解释的现象有 (填序号).
①有两个钉子就可以把木条固定在墙上;
②A从地到B地架设电线,总是尽可能沿着线段AB架设;
③植树时,只要定出两棵树的位置,就能确定同一行所在的直线;
④把弯曲的公路改直,就能缩短路程,
三.解答题
17.如图所示,工厂A与工厂B想在公路m旁修建一座共用的仓库O,并且要求O到A与O到B的距离之和最短,请你在m上确定仓库应修建的O点位置,同时说明你选择该点的理由.
18.(南关区校级月考)请你判断下列两个生活情景所蕴含的数学道理.
情景一:如图,小明家到学校有3条路可走,一般情况下,小明通常走第二条路,其中的数学道理是 .
情景二:同学们做体操时,为了保证一队同学站成一条直线,先让两个同学站好不动,其他同学依次往后站,要求目视前方只能看到各自前面的那个同学,请你说明其中的道理: .
19.如图,线段AB=8cm,C是线段AB上一点,AC=3cm,M是AB的中点,N是AC的中点.
(1)求线段CM、NM的长;
(2)若线段AC=m,线段BC=n,求MN的长度(m<n用含m,n的代数式表示).
20.(1)如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点,求线段MN的长度;
(2)已知点C在线段BA的延长线上,点M,N分别是AC,BC的中点,设BC﹣AC=a,请根据题意画出图形并求MN的长度;
(3)在(1)的条件下,动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
答案
一.选择题
C.C.C.C.B.B.A.
二.填空题
8.<.
9.>.
10.8cm.
11.5cm或1cm.
12.2.
13.2cm或8.
14.4或12.
15.A.
16.②④.
三.解答题
17.解:如图,连接AB交直线m于点O,
则O点即为所求的点.
∴OA+OB最短.
18.解:情景一:如图,小明家到学校有3条路可走,一般情况下,小明通常走第二条路,其中的数学道理是两点之间线段最短;
故答案为:两点之间线段最短;
故答案为:两点确定一条直线.
19.解:(1)∵AB=8cm,M是AB的中点,
∴AM=AB=6cm,
∴CM=AM﹣AC=4﹣3=1(cm);
∴AM=AB=4cm,AN=AC=1.6cm,
(2)∵AC=m,BC=n,
∵M是AB的中点,N是AC的中点,
∴MN=AM﹣AN=(m+n)﹣m=n.
20.解:(1)∵线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点,
∴CM=AC=5厘米,CN=BC=3厘米,
(2)如图,∵点M,N分别是AC,BC的中点,
∴MN=CN﹣CM=(BC﹣AC)=a;
(3)①当0<t≤8时,C是线段PQ的中点,得
10﹣2t=6﹣t,解得t=4;
②当5<t≤时,P为线段CQ的中点,2t﹣10=16﹣3t,解得t=;
③当<t≤6时,Q为线段PC的中点,6﹣t=3t﹣16,解得t=;
④当3<t≤8时,C为线段PQ的中点,2t﹣10=t﹣6,解得t=4(舍),
综上所述:t=4或或.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
