浙教版七年级数学上册试题 6.8余角和补角(含答案)
文档属性
| 名称 | 浙教版七年级数学上册试题 6.8余角和补角(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 68.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-30 02:13:49 | ||
图片预览




文档简介
6.8余角和补角
一.选择题
1.一个角的余角是44°,这个角的补角是( )
A.134° B.136° C.156° D.146°
2.若锐角α的补角是140°,则锐角α的余角是( )
A.30° B.40° C.50° D.60°
3.已知∠1和∠2互为余角,且∠2与∠3互补,∠1=60°,则∠3为( )
A.120° B.60° C.30° D.150°
4.下列叙述正确的是( )
A.一个钝角和一个锐角一定互为补角
B.每一个锐角都有余角
C.两个锐角一定互为余角
D.一个钝角的余角是锐角
5.下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,② B.①,②,③ C.③,④,② D.③,④
6.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A. B. C. D.
7.已知锐角α,那么∠α的补角与∠α的余角的差是( )
A.90° B.120° C.60°+α D.180°﹣α
8.如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有( )
A.5对 B.4对 C.3对 D.2对
如图所示,∠AOE=∠EOB=∠DOC=90°,则下列说法不正确的是( )
A.∠1与∠2,∠3与∠4互为余角
B.∠4=∠3,∠2=∠4
C.∠1与∠4,∠2与∠3互为余角
D.∠1=∠3,∠2=∠4
10.如果∠1与∠2互余,∠3与∠4互补,且∠1=∠3,那么( )
A.∠2+90°=∠4 B.∠2=∠4 C.∠2与∠4互余 D.∠2与∠4互补
二.填空题
11.如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:其中表示∠B余角的式子有 .(填序号)
①90°﹣∠B;
②∠A﹣90°;
③(∠A﹣∠B);
④(∠A+∠B).
12.已知∠1与∠2互余,∠2与∠3互补,若∠1=33°27′16″,则∠3= .
13.已知∠α与∠β互补,且∠α与∠β的差是70°,则∠α= ,∠β= .
14.已知:如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,图形中相等的角有 对,互余的角有 对.
15.如右图,∠BAD和∠CAE都是直角,若∠BAE=135°17′42″,则∠CAD= (用度、分、秒表示)
16.如图所示,O是直线AB与CD的交点,∠BOM:∠DOM=1:2,∠CON=90°,∠NOM=68°,则∠BOD= °.
三.解答题
17.按要求解答下列各题.
(1)一个角的余角比它的补角的大1°,求这个角的度数;
(2)一个角的余角比这个角的补角的还小10°,求这个角的余角及这个角的补角.
18.下列说法中,哪些是正确的?说明理由.
(1)互余且相等的两个角各是45°;
(2)一个角的余角一定小于这个角的补角;
(3)如果∠1+∠2=∠3,那么∠1的余角与∠2的余角的和等于∠3的余角;
(4)如果∠1+∠2=∠3,那么∠1的余角与∠2的余角的和等于∠3的补角.
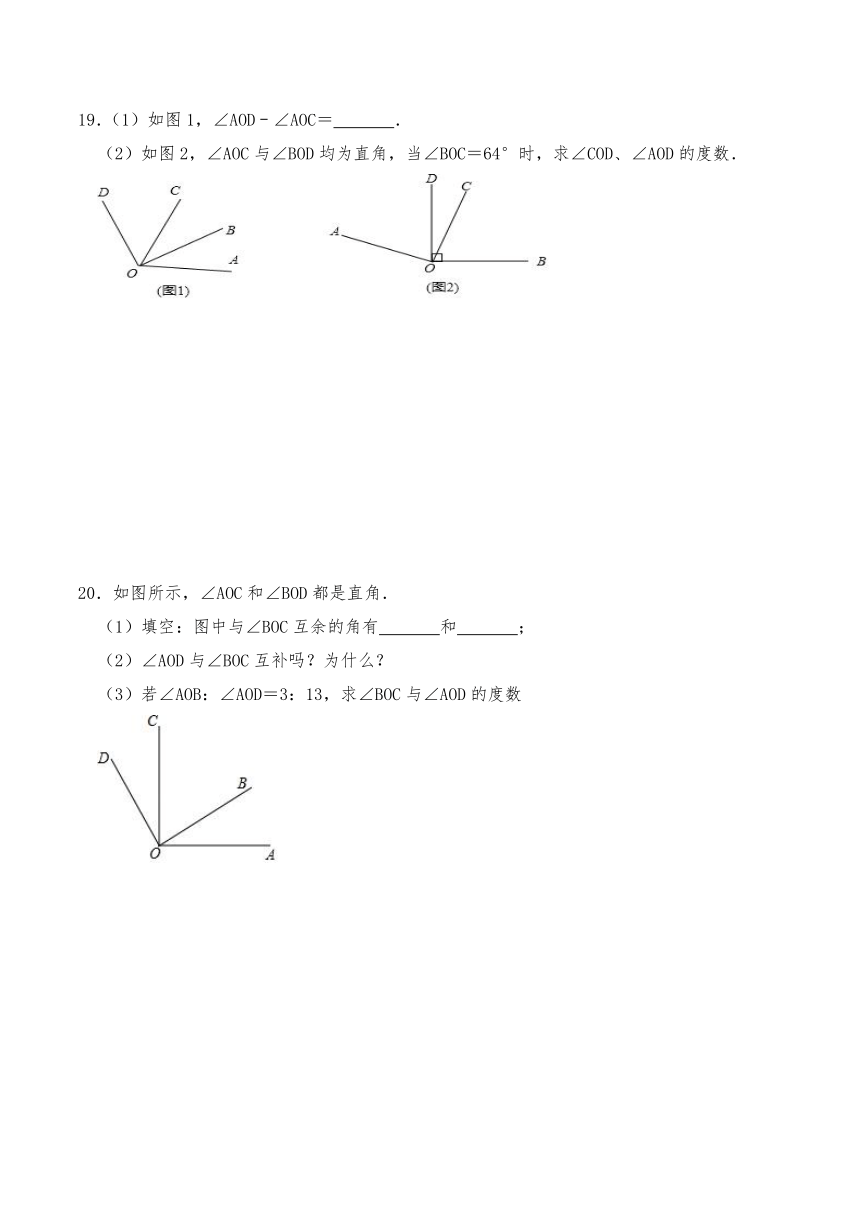
19.(1)如图1,∠AOD﹣∠AOC= .
(2)如图2,∠AOC与∠BOD均为直角,当∠BOC=64°时,求∠COD、∠AOD的度数.
20.如图所示,∠AOC和∠BOD都是直角.
(1)填空:图中与∠BOC互余的角有 和 ;
(2)∠AOD与∠BOC互补吗?为什么?
(3)若∠AOB:∠AOD=3:13,求∠BOC与∠AOD的度数
21.如图,已知直线AB上一点O,∠AOC=∠DOE=90°,∠DOC=∠EOB.
(1)求证:∠AOD=∠COE
证明(法1):∵∠AOC=∠DOE=90°(已知)
∴∠AOD+∠COD=90°
∠COE+∠COD=90°
∴∠AOD=∠COE( )
(法2)∵∠AOC=90°(已知)
∴∠COB=90°
∴∠AOD+∠DOC=90°
∠COE+∠EOB=90°
∵∠DOC=∠EOB(已知)
∴∠AOD=∠COE( )
(2)若∠COE=∠BOD,求∠AOE、∠COD的度数.
22.如图,将一副直角三角尺的直角顶点C叠放在一起.
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)若保持三角尺BCE不动,三角尺ACD的CD边与CB边重合,然后将三角尺ACD绕点C按逆时针方向
任意转动一个角度∠BCD.设∠BCD=α(0°<α<90°)
①∠ACB能否是∠DCE的4倍?若能求出α的值;若不能说明理由.
②三角尺ACD转动中,∠BCD每秒转动3°,当∠DCE=21°时,转动了多少秒?
答案
一.选择题
A.C.D.B.A.A.A.A.B.A.
二.填空题
11.①②③.
12.123°27′16″.
13.125°,55°.
14.5;4.
15.44°42' 18''.
16.33.
三.解答题
17.解:(1)设这个角的度数为x,则这个角的余角为90﹣x,补角为180﹣x,由题意得,
90﹣x=×(180﹣x)+1
解得x=63;
答:这个角的度数为63°.
(2)设这个角的度数为x,则这个角的余角为90﹣x,补角为180﹣x,由题意得,
90﹣x=×(180﹣x)﹣10
解得x=60,
则90﹣x=30,180﹣x=120;
答:这个角的余角30°,这个角的补角120°.
18.解:(1)互余且相等的两个角都是45°,正确,45°+45°=90°;
(2)一个角的余角一定小于这个角的补角,正确,因为一个角的补角比它的余角大90°;
(3)如果∠1+∠2=∠3,那么∠1的余角与∠2的余角的和等于∠3的余角,错误,∠3的余角余角=90°﹣(∠1+∠2),∠1的余角与∠2的余角的和=(90°﹣∠1)+(90°﹣∠2)=180°﹣(∠1+∠2);
(4)如果∠1+∠2=∠3,那么∠1的余角与∠2的余角的和等于∠3的补角,正确,因为∠3的补角=180°﹣(∠1+∠2)=(90°﹣∠1)+(90°﹣∠2).
故正确的说法有(1)(2)(3).
19.解:(1)如图1,∠AOD﹣∠AOC=∠COD;
(2)∵∠BOD=90°,∠BOC=64°,
∴∠COD=90°﹣64°=26°,
∵∠AOC=90°,
∴∠AOD=64°,∠COD=26°,∠AOD=64°.
故答案为:∠COD.
20.解:(1)因为∠AOC和∠BOD都是直角,
所以∠AOB+∠BOC=∠COD+∠BOC=90°,
所以∠BOC与∠AOB互余,∠BOC与∠COD互余,
故答案为:∠AOB、∠COD;
(2)∠AOD与∠BOC互补,理由如下:
因为∠AOC和∠BOD都是直角,
所以∠AOB+∠BOC=∠COD+∠BOC=90°,
又因为∠AOD=∠AOB+∠BOC+∠COD,
所以∠AOD+∠BOC=∠AOB+∠BOC+∠COD+∠BOC=180°,
所以∠AOD与∠BOC互补;
(3)设∠AOB=3x°、则∠AOD=13x°,
所以∠BOD=∠AOD﹣∠AOB=13x﹣3x=10x=90,
即x=9,
所以∠AOD=13x=117°,
由(2)可知∠AOD与∠BOC互补,
所以∠BOC=180°﹣117°=63°.
21.解:(1)证明(法1):∵∠AOC=∠DOE=90°(已知)
∴∠AOD+∠COD=90°
∠COE+∠COD=90°
∴∠AOD=∠COE(同角的余角相等)
(法2)∵∠AOC=90°(已知)
∴∠COB=90°
∴∠AOD+∠DOC=90°
∠COE+∠EOB=90°
∵∠DOC=∠EOB(已知)
∴∠AOD=∠COE(等角的余角相等).
故答案为:同角的余角相等;等角的余角相等
(2)设∠BOD=5x,∠AOD=x,
∴5x+x=180°,
解得x=30°,
∴∠BOD=150°,
∠COD=90°﹣0°=60°,
∠BOE=∠COD=60°,
∠AOE=120°.
22.解:(1)∵∠ACD=∠ECB=90°,∠DCE=35°,
∴∠ACB=180°﹣35°=145°.
∵∠ACD=∠ECB=90°,∠ACB=140°,
∴∠DCE=180°﹣140°=40°.
故答案为:145°,40°;
(2)∠ACB+∠DCE=180°或互补,
理由:∵∠ACE+∠ECD+∠DCB+∠ECD=180.
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠DCE=180°,即∠ACB与∠DCE互补.
(3)①当∠ACB是∠DCE的4倍,
∴设∠ACB=4x,∠DCE=x,
∵∠ACB+∠DCE=180°,
∴4x+x=180°
解得:x=36°,
∴α=90°﹣36°=54°;
②设当∠DCE=21°时,转动了t秒,
∵∠BCD+∠DCE=90°,
∴3t+21=90,
t=23°,
答:当∠DCE=21°时,转动了23秒.
一.选择题
1.一个角的余角是44°,这个角的补角是( )
A.134° B.136° C.156° D.146°
2.若锐角α的补角是140°,则锐角α的余角是( )
A.30° B.40° C.50° D.60°
3.已知∠1和∠2互为余角,且∠2与∠3互补,∠1=60°,则∠3为( )
A.120° B.60° C.30° D.150°
4.下列叙述正确的是( )
A.一个钝角和一个锐角一定互为补角
B.每一个锐角都有余角
C.两个锐角一定互为余角
D.一个钝角的余角是锐角
5.下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,② B.①,②,③ C.③,④,② D.③,④
6.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A. B. C. D.
7.已知锐角α,那么∠α的补角与∠α的余角的差是( )
A.90° B.120° C.60°+α D.180°﹣α
8.如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有( )
A.5对 B.4对 C.3对 D.2对
如图所示,∠AOE=∠EOB=∠DOC=90°,则下列说法不正确的是( )
A.∠1与∠2,∠3与∠4互为余角
B.∠4=∠3,∠2=∠4
C.∠1与∠4,∠2与∠3互为余角
D.∠1=∠3,∠2=∠4
10.如果∠1与∠2互余,∠3与∠4互补,且∠1=∠3,那么( )
A.∠2+90°=∠4 B.∠2=∠4 C.∠2与∠4互余 D.∠2与∠4互补
二.填空题
11.如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:其中表示∠B余角的式子有 .(填序号)
①90°﹣∠B;
②∠A﹣90°;
③(∠A﹣∠B);
④(∠A+∠B).
12.已知∠1与∠2互余,∠2与∠3互补,若∠1=33°27′16″,则∠3= .
13.已知∠α与∠β互补,且∠α与∠β的差是70°,则∠α= ,∠β= .
14.已知:如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,图形中相等的角有 对,互余的角有 对.
15.如右图,∠BAD和∠CAE都是直角,若∠BAE=135°17′42″,则∠CAD= (用度、分、秒表示)
16.如图所示,O是直线AB与CD的交点,∠BOM:∠DOM=1:2,∠CON=90°,∠NOM=68°,则∠BOD= °.
三.解答题
17.按要求解答下列各题.
(1)一个角的余角比它的补角的大1°,求这个角的度数;
(2)一个角的余角比这个角的补角的还小10°,求这个角的余角及这个角的补角.
18.下列说法中,哪些是正确的?说明理由.
(1)互余且相等的两个角各是45°;
(2)一个角的余角一定小于这个角的补角;
(3)如果∠1+∠2=∠3,那么∠1的余角与∠2的余角的和等于∠3的余角;
(4)如果∠1+∠2=∠3,那么∠1的余角与∠2的余角的和等于∠3的补角.
19.(1)如图1,∠AOD﹣∠AOC= .
(2)如图2,∠AOC与∠BOD均为直角,当∠BOC=64°时,求∠COD、∠AOD的度数.
20.如图所示,∠AOC和∠BOD都是直角.
(1)填空:图中与∠BOC互余的角有 和 ;
(2)∠AOD与∠BOC互补吗?为什么?
(3)若∠AOB:∠AOD=3:13,求∠BOC与∠AOD的度数
21.如图,已知直线AB上一点O,∠AOC=∠DOE=90°,∠DOC=∠EOB.
(1)求证:∠AOD=∠COE
证明(法1):∵∠AOC=∠DOE=90°(已知)
∴∠AOD+∠COD=90°
∠COE+∠COD=90°
∴∠AOD=∠COE( )
(法2)∵∠AOC=90°(已知)
∴∠COB=90°
∴∠AOD+∠DOC=90°
∠COE+∠EOB=90°
∵∠DOC=∠EOB(已知)
∴∠AOD=∠COE( )
(2)若∠COE=∠BOD,求∠AOE、∠COD的度数.
22.如图,将一副直角三角尺的直角顶点C叠放在一起.
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)若保持三角尺BCE不动,三角尺ACD的CD边与CB边重合,然后将三角尺ACD绕点C按逆时针方向
任意转动一个角度∠BCD.设∠BCD=α(0°<α<90°)
①∠ACB能否是∠DCE的4倍?若能求出α的值;若不能说明理由.
②三角尺ACD转动中,∠BCD每秒转动3°,当∠DCE=21°时,转动了多少秒?
答案
一.选择题
A.C.D.B.A.A.A.A.B.A.
二.填空题
11.①②③.
12.123°27′16″.
13.125°,55°.
14.5;4.
15.44°42' 18''.
16.33.
三.解答题
17.解:(1)设这个角的度数为x,则这个角的余角为90﹣x,补角为180﹣x,由题意得,
90﹣x=×(180﹣x)+1
解得x=63;
答:这个角的度数为63°.
(2)设这个角的度数为x,则这个角的余角为90﹣x,补角为180﹣x,由题意得,
90﹣x=×(180﹣x)﹣10
解得x=60,
则90﹣x=30,180﹣x=120;
答:这个角的余角30°,这个角的补角120°.
18.解:(1)互余且相等的两个角都是45°,正确,45°+45°=90°;
(2)一个角的余角一定小于这个角的补角,正确,因为一个角的补角比它的余角大90°;
(3)如果∠1+∠2=∠3,那么∠1的余角与∠2的余角的和等于∠3的余角,错误,∠3的余角余角=90°﹣(∠1+∠2),∠1的余角与∠2的余角的和=(90°﹣∠1)+(90°﹣∠2)=180°﹣(∠1+∠2);
(4)如果∠1+∠2=∠3,那么∠1的余角与∠2的余角的和等于∠3的补角,正确,因为∠3的补角=180°﹣(∠1+∠2)=(90°﹣∠1)+(90°﹣∠2).
故正确的说法有(1)(2)(3).
19.解:(1)如图1,∠AOD﹣∠AOC=∠COD;
(2)∵∠BOD=90°,∠BOC=64°,
∴∠COD=90°﹣64°=26°,
∵∠AOC=90°,
∴∠AOD=64°,∠COD=26°,∠AOD=64°.
故答案为:∠COD.
20.解:(1)因为∠AOC和∠BOD都是直角,
所以∠AOB+∠BOC=∠COD+∠BOC=90°,
所以∠BOC与∠AOB互余,∠BOC与∠COD互余,
故答案为:∠AOB、∠COD;
(2)∠AOD与∠BOC互补,理由如下:
因为∠AOC和∠BOD都是直角,
所以∠AOB+∠BOC=∠COD+∠BOC=90°,
又因为∠AOD=∠AOB+∠BOC+∠COD,
所以∠AOD+∠BOC=∠AOB+∠BOC+∠COD+∠BOC=180°,
所以∠AOD与∠BOC互补;
(3)设∠AOB=3x°、则∠AOD=13x°,
所以∠BOD=∠AOD﹣∠AOB=13x﹣3x=10x=90,
即x=9,
所以∠AOD=13x=117°,
由(2)可知∠AOD与∠BOC互补,
所以∠BOC=180°﹣117°=63°.
21.解:(1)证明(法1):∵∠AOC=∠DOE=90°(已知)
∴∠AOD+∠COD=90°
∠COE+∠COD=90°
∴∠AOD=∠COE(同角的余角相等)
(法2)∵∠AOC=90°(已知)
∴∠COB=90°
∴∠AOD+∠DOC=90°
∠COE+∠EOB=90°
∵∠DOC=∠EOB(已知)
∴∠AOD=∠COE(等角的余角相等).
故答案为:同角的余角相等;等角的余角相等
(2)设∠BOD=5x,∠AOD=x,
∴5x+x=180°,
解得x=30°,
∴∠BOD=150°,
∠COD=90°﹣0°=60°,
∠BOE=∠COD=60°,
∠AOE=120°.
22.解:(1)∵∠ACD=∠ECB=90°,∠DCE=35°,
∴∠ACB=180°﹣35°=145°.
∵∠ACD=∠ECB=90°,∠ACB=140°,
∴∠DCE=180°﹣140°=40°.
故答案为:145°,40°;
(2)∠ACB+∠DCE=180°或互补,
理由:∵∠ACE+∠ECD+∠DCB+∠ECD=180.
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠DCE=180°,即∠ACB与∠DCE互补.
(3)①当∠ACB是∠DCE的4倍,
∴设∠ACB=4x,∠DCE=x,
∵∠ACB+∠DCE=180°,
∴4x+x=180°
解得:x=36°,
∴α=90°﹣36°=54°;
②设当∠DCE=21°时,转动了t秒,
∵∠BCD+∠DCE=90°,
∴3t+21=90,
t=23°,
答:当∠DCE=21°时,转动了23秒.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
