九年级数学上册试题 3.4 圆心角-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 3.4 圆心角-浙教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 160.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 00:00:00 | ||
图片预览

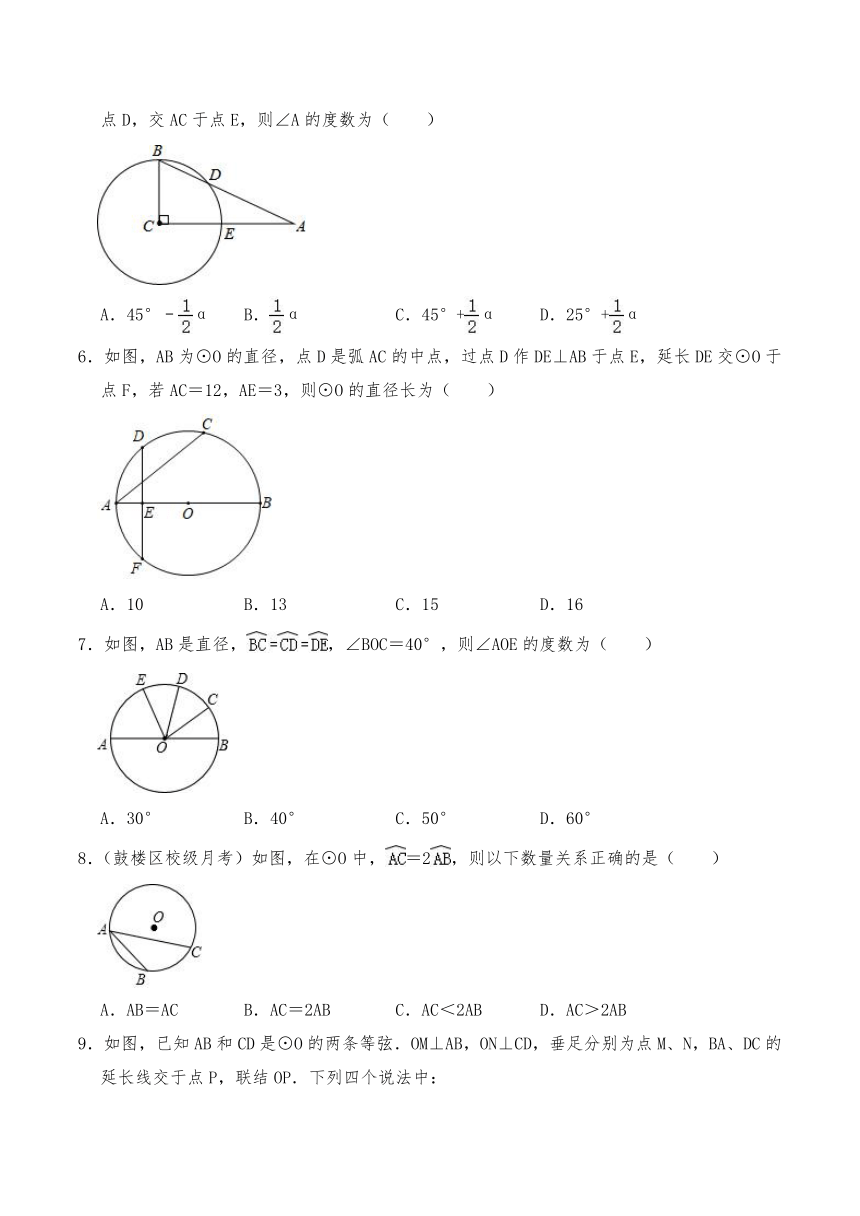


文档简介
3.4 圆心角
一.选择题
1.下图中∠ACB是圆心角的是( )
A. B. C. D.
2.下列语句,错误的是( )
A.直径是弦
B.相等的圆心角所对的弧相等
C.弦的垂直平分线一定经过圆心
D.平分弧的半径垂直于弧所对的弦
3.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠OFE的度数是( )
A.30° B.20° C.40° D.35°
4.如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心O2,恰好在大量角器的圆周上,设图中两圆周的交点为P,且点P在小量角器上对应的刻度为63°,那么点P在大量角器上对应的刻度为(只考虑小于90°的角)( )
A.54° B.55° C.56° D.57°
5.如图,在△ABC中,∠C=90°,的度数为α,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E,则∠A的度数为( )
A.45°﹣α B.α C.45°+α D.25°+α
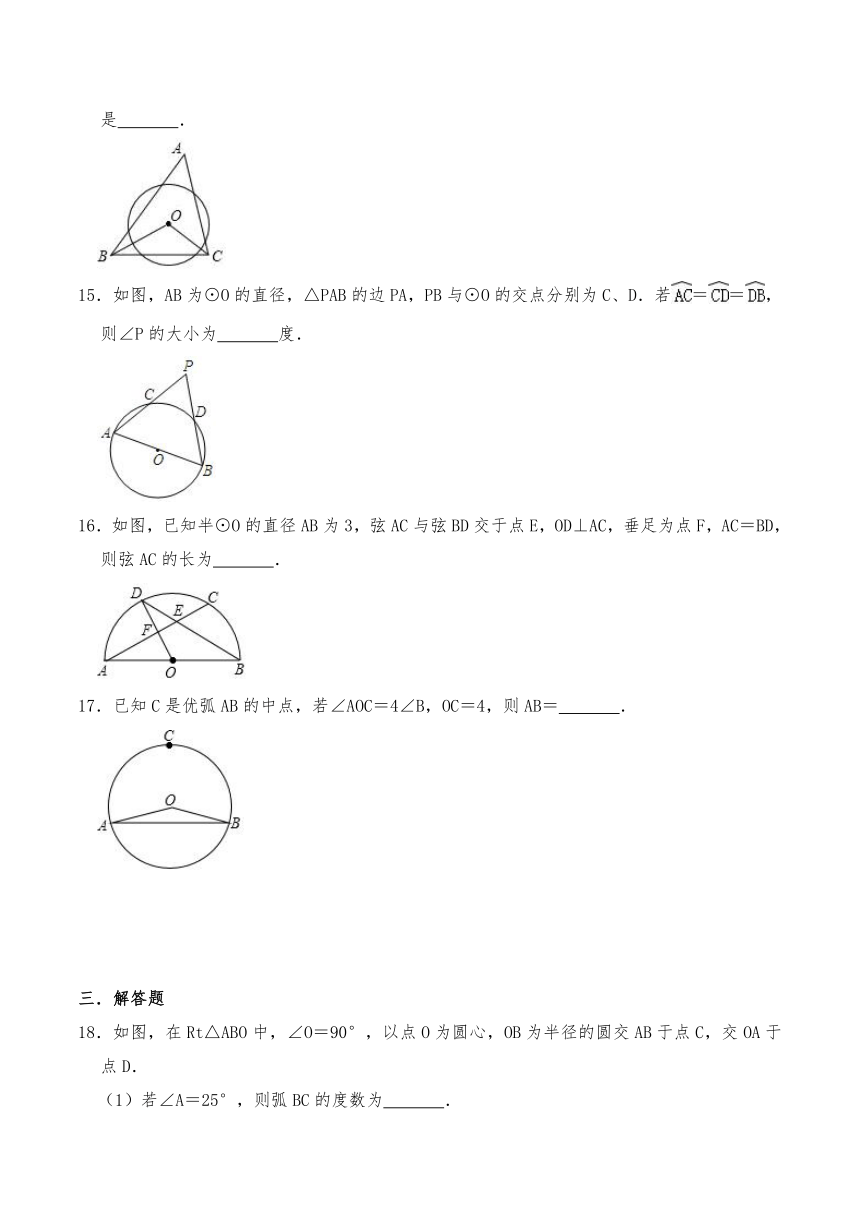
6.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AC=12,AE=3,则⊙O的直径长为( )
A.10 B.13 C.15 D.16
7.如图,AB是直径,,∠BOC=40°,则∠AOE的度数为( )
A.30° B.40° C.50° D.60°
8.(鼓楼区校级月考)如图,在⊙O中,=2,则以下数量关系正确的是( )
A.AB=AC B.AC=2AB C.AC<2AB D.AC>2AB
9.如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:
①;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是( )
A.1 B.2 C.3 D.4
10.如图,点A是半圆上的一个三等分点,点B为弧AD的中点,P是直径CD上一动点,⊙O的半径是2,则PA+PB的最小值为( )
A.2 B. C. D.
二.填空题
11.长度等于6的弦所对的圆心角是90°,则该圆半径为 .
12.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE= .
13.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为40°,则的度数是 .
14.如图,在△ABC中,∠BAC=52°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是 .
15.如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C、D.若==,则∠P的大小为 度.
16.如图,已知半⊙O的直径AB为3,弦AC与弦BD交于点E,OD⊥AC,垂足为点F,AC=BD,则弦AC的长为 .
17.已知C是优弧AB的中点,若∠AOC=4∠B,OC=4,则AB= .
三.解答题
18.如图,在Rt△ABO中,∠O=90°,以点O为圆心,OB为半径的圆交AB于点C,交OA于点D.
(1)若∠A=25°,则弧BC的度数为 .
(2)若OB=3,OA=4,求BC的长.
19.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.求证:AE=CE.
20.如图,以 ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧和弧是否相等,并说明理由.
21.如图,A、B是⊙O上的两点,∠AOB=120°,C是弧AB的中点,CE⊥OA交⊙O于点E,连接AE.求证:AE=AO.
22.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
答案
一.选择题
B.B.D.A.A.C.D.C.D.D.
二.填空题
11.6.
12.3.
13.120°.
14.116°.
15.60.
16.;
17.4.
三.解答题
18.解:(1)连接OC.
∵∠AOB=90°,∠A=25°,
∴∠B=90°﹣∠A=65°,
∵OB=OC,
∴∠B=∠OCB=65°,
∴∠BCO=180°﹣65°﹣65°=50°,
∴弧BC的度数为50°,
故答案为50°.
(2)如图,作OH⊥BC于H.
在Rt△AOB中,∵∠AOB=90°,OA=4,OB=3,
∴AB===5,
∵S△AOB= OB OA= AB OH,
∴OH==,
∴BH===,
∵OH⊥BC,
∴BH=CH,
∴BC=2BH=.
19.证明:解法一:∵AB=CD,
∴,即,
∴,
∴AD=BC,
又∵∠ADE=∠CBE,∠A=∠C,
∴△ADE≌△CBE(ASA),
∴AE=CE.
解法二:连接AC,
∵AB=CD,
∴,即,
∴,
∴AD=BC,
又∵AB=CD,AC=CA,
∴△ABC≌△CDA(SSS),
∴∠BAC=∠ACD,
∴AE=CE.
20.解:=,
理由:连接AE.
∴AB=AE,
∴∠B=∠AEB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,
∴.
21.证明:连OC,OA,如图,
∵∠AOB=120°,C是弧AB的中点,
∴∠AOC=60°,
∵OA=OC,
∴△AOC为等边三角形,
∴AC=AO,
∵OA⊥CE,
∴=,
∴AE=AC,
∴AE=AO.
22.证明:(1)连接OB、OC,
∵AB=AC,OC=OB,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42
解得:x=5,OE=3,
∴半径OA的长=5.
一.选择题
1.下图中∠ACB是圆心角的是( )
A. B. C. D.
2.下列语句,错误的是( )
A.直径是弦
B.相等的圆心角所对的弧相等
C.弦的垂直平分线一定经过圆心
D.平分弧的半径垂直于弧所对的弦
3.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠OFE的度数是( )
A.30° B.20° C.40° D.35°
4.如图,将大小不同的两块量角器的零度线对齐,且小量角器的中心O2,恰好在大量角器的圆周上,设图中两圆周的交点为P,且点P在小量角器上对应的刻度为63°,那么点P在大量角器上对应的刻度为(只考虑小于90°的角)( )
A.54° B.55° C.56° D.57°
5.如图,在△ABC中,∠C=90°,的度数为α,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E,则∠A的度数为( )
A.45°﹣α B.α C.45°+α D.25°+α
6.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AC=12,AE=3,则⊙O的直径长为( )
A.10 B.13 C.15 D.16
7.如图,AB是直径,,∠BOC=40°,则∠AOE的度数为( )
A.30° B.40° C.50° D.60°
8.(鼓楼区校级月考)如图,在⊙O中,=2,则以下数量关系正确的是( )
A.AB=AC B.AC=2AB C.AC<2AB D.AC>2AB
9.如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:
①;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是( )
A.1 B.2 C.3 D.4
10.如图,点A是半圆上的一个三等分点,点B为弧AD的中点,P是直径CD上一动点,⊙O的半径是2,则PA+PB的最小值为( )
A.2 B. C. D.
二.填空题
11.长度等于6的弦所对的圆心角是90°,则该圆半径为 .
12.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE= .
13.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为40°,则的度数是 .
14.如图,在△ABC中,∠BAC=52°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是 .
15.如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C、D.若==,则∠P的大小为 度.
16.如图,已知半⊙O的直径AB为3,弦AC与弦BD交于点E,OD⊥AC,垂足为点F,AC=BD,则弦AC的长为 .
17.已知C是优弧AB的中点,若∠AOC=4∠B,OC=4,则AB= .
三.解答题
18.如图,在Rt△ABO中,∠O=90°,以点O为圆心,OB为半径的圆交AB于点C,交OA于点D.
(1)若∠A=25°,则弧BC的度数为 .
(2)若OB=3,OA=4,求BC的长.
19.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.求证:AE=CE.
20.如图,以 ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断弧和弧是否相等,并说明理由.
21.如图,A、B是⊙O上的两点,∠AOB=120°,C是弧AB的中点,CE⊥OA交⊙O于点E,连接AE.求证:AE=AO.
22.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
答案
一.选择题
B.B.D.A.A.C.D.C.D.D.
二.填空题
11.6.
12.3.
13.120°.
14.116°.
15.60.
16.;
17.4.
三.解答题
18.解:(1)连接OC.
∵∠AOB=90°,∠A=25°,
∴∠B=90°﹣∠A=65°,
∵OB=OC,
∴∠B=∠OCB=65°,
∴∠BCO=180°﹣65°﹣65°=50°,
∴弧BC的度数为50°,
故答案为50°.
(2)如图,作OH⊥BC于H.
在Rt△AOB中,∵∠AOB=90°,OA=4,OB=3,
∴AB===5,
∵S△AOB= OB OA= AB OH,
∴OH==,
∴BH===,
∵OH⊥BC,
∴BH=CH,
∴BC=2BH=.
19.证明:解法一:∵AB=CD,
∴,即,
∴,
∴AD=BC,
又∵∠ADE=∠CBE,∠A=∠C,
∴△ADE≌△CBE(ASA),
∴AE=CE.
解法二:连接AC,
∵AB=CD,
∴,即,
∴,
∴AD=BC,
又∵AB=CD,AC=CA,
∴△ABC≌△CDA(SSS),
∴∠BAC=∠ACD,
∴AE=CE.
20.解:=,
理由:连接AE.
∴AB=AE,
∴∠B=∠AEB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B=∠GAF,∠FAE=∠AEB,
∴∠GAF=∠FAE,
∴.
21.证明:连OC,OA,如图,
∵∠AOB=120°,C是弧AB的中点,
∴∠AOC=60°,
∵OA=OC,
∴△AOC为等边三角形,
∴AC=AO,
∵OA⊥CE,
∴=,
∴AE=AC,
∴AE=AO.
22.证明:(1)连接OB、OC,
∵AB=AC,OC=OB,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42
解得:x=5,OE=3,
∴半径OA的长=5.
同课章节目录
