九年级数学上册试题 3.6 圆内接四边形-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 3.6 圆内接四边形-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 174.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 10:47:35 | ||
图片预览



文档简介
3.6 圆内接四边形
一.选择题
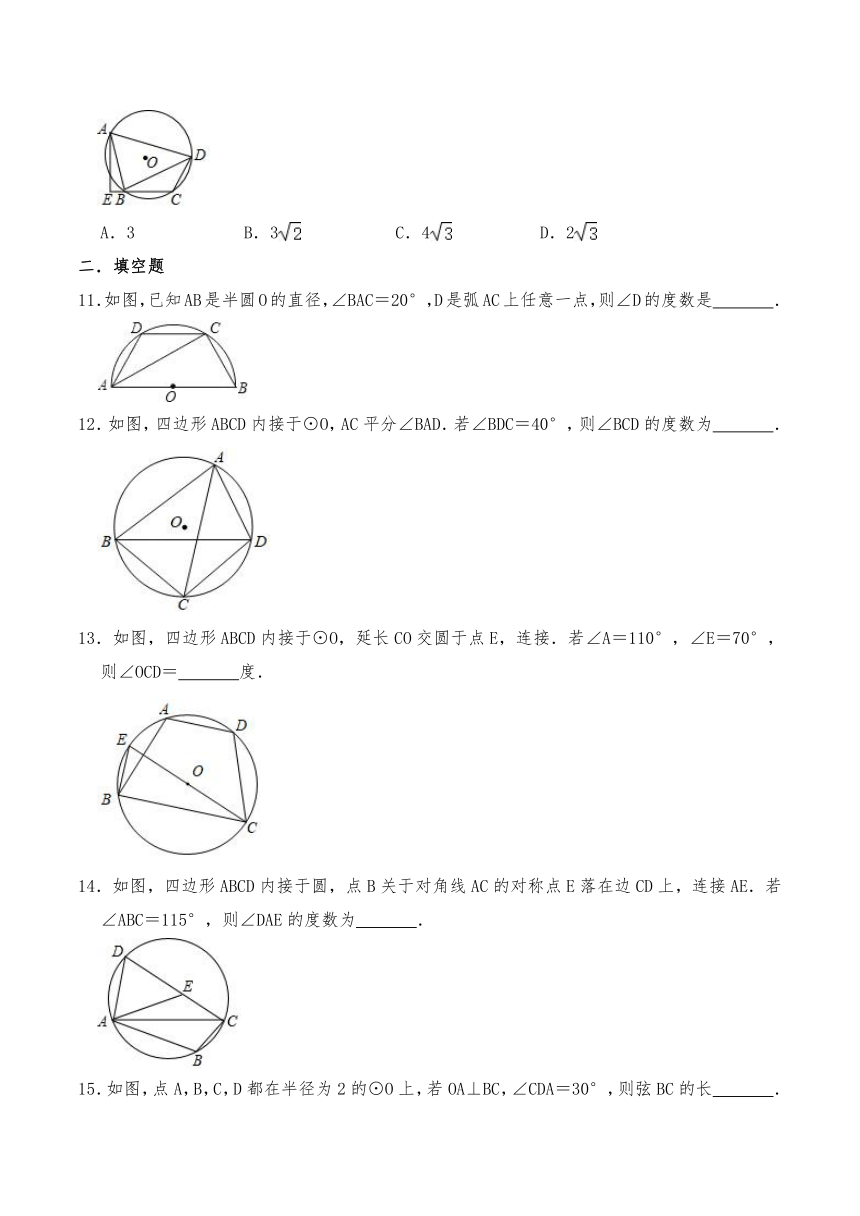
1.如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )
A.70° B.110° C.130° D.140°
2.如图,四边形ABCD内接于⊙O,∠BOD=110°,那么∠BCD等于( )
A.110° B.135° C.55° D.125°
3.如图,点A、B、C、D在⊙O上,四边形OBCD是平行四边形,则∠A的大小为( )
A.30° B.45° C.60° D.无法确定
4.如图,四边形ABCD是半圆的内接四边形,AB是直径,点C是的中点,如果∠DAB=70°,则∠ABC的度数等于( )
A.55° B.60° C.65° D.70°
5.如图,四边形ABCD内接于圆,并有:::=4:5:6:5,则∠B的度数为( )
A.90° B.95° C.99° D.100°
6.如图,五边形ABCDE内接于⊙O,若∠CAD=35°,则∠B+∠E的度数是( )
A.210° B.215° C.235° D.250°
7.已知圆内接四边形ABCD中,∠A:∠B:∠C=1:2:3,则∠D的大小是( )
A.45° B.60° C.90° D.135°
8.如图,四边形ABCD内接于⊙O,AB是直径,BC∥OD,若∠C=130°,则∠B的度数为( )
A.50° B.60° C.70° D.80°
9.下列说法正确的有( )
①平分弦的直径垂直于弦.②半圆所对的圆周角是直角.③一条弧所对的圆周角等于它所对的圆心角的一半.④在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等.⑤圆内接平行四边形是矩形.
A.1个 B.2个 C.3个 D.4个
10.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE=,则AE=( )
A.3 B.3 C.4 D.2
二.填空题
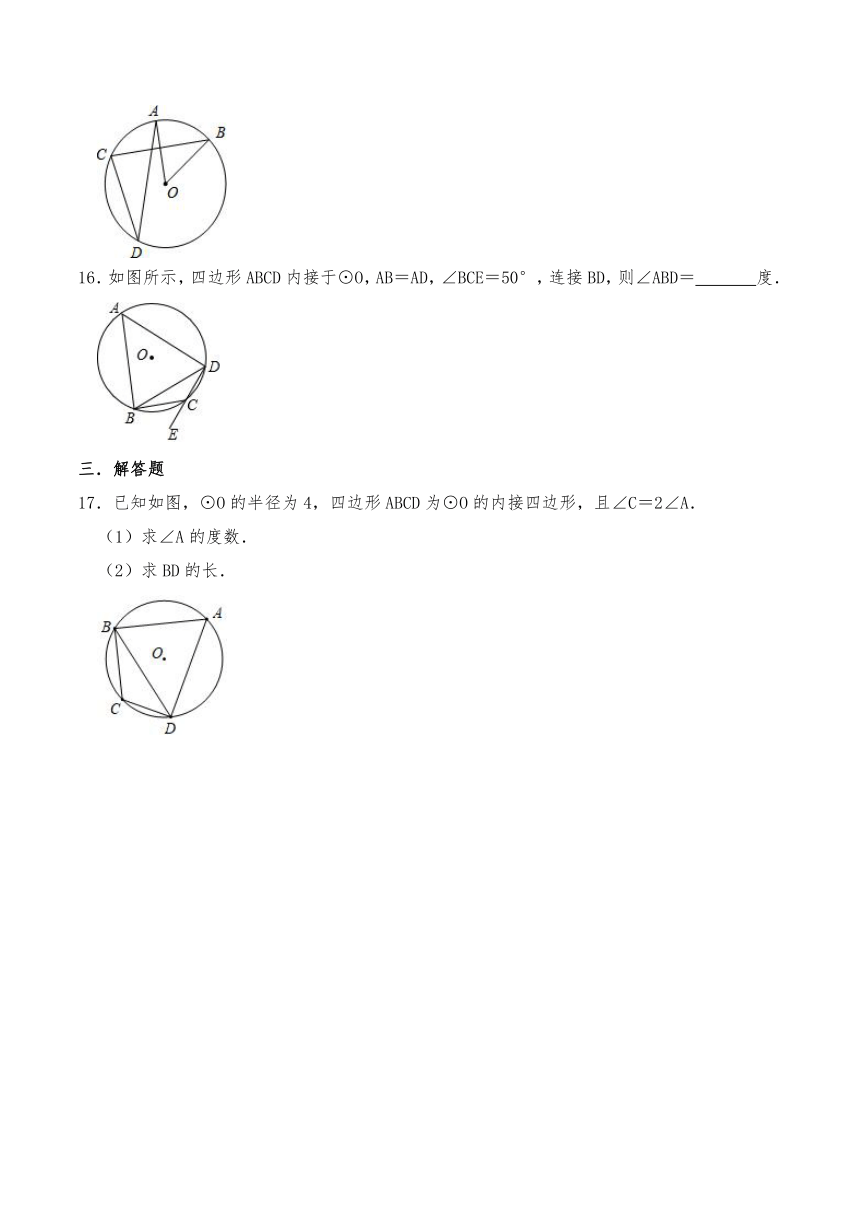
11.如图,已知AB是半圆O的直径,∠BAC=20°,D是弧AC上任意一点,则∠D的度数是 .
12.如图,四边形ABCD内接于⊙O,AC平分∠BAD.若∠BDC=40°,则∠BCD的度数为 .
13.如图,四边形ABCD内接于⊙O,延长CO交圆于点E,连接.若∠A=110°,∠E=70°,则∠OCD= 度.
14.如图,四边形ABCD内接于圆,点B关于对角线AC的对称点E落在边CD上,连接AE.若∠ABC=115°,则∠DAE的度数为 .
15.如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长 .
16.如图所示,四边形ABCD内接于⊙O,AB=AD,∠BCE=50°,连接BD,则∠ABD= 度.
三.解答题
17.已知如图,⊙O的半径为4,四边形ABCD为⊙O的内接四边形,且∠C=2∠A.
(1)求∠A的度数.
(2)求BD的长.
18.如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,AB=AC.
(1)求证:DE平分∠CDF;
(2)求证:∠ACD=∠AEB.
19.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=40°,求∠BAD的度数;
(2)求证:∠1=∠2.
20.四边形ABCD内接于⊙O,AC为其中一条对角线.
(Ⅰ)如图①,若∠BAD=70°,BC=CD.求∠CAD的大小;
(Ⅱ)如图②,若AD经过圆心O,连接OC,AB=BC,OC∥AB,求∠ACO的大小.
21.已知,如图△ABC中,AB=AC,D是边BC上一点,BD<DC,过点A、D、C三点的⊙O交AB于点F,点E在上,连接DF、AE、DE、CE.
(1)求证:△BDF是等腰三角形;
(2)若,请用题意可以推出的结论说明命题:“一组对边相等,且一组对角相等的四边形是平行四边形”是假命题.
22.已知四边形ABCD内接于⊙O,∠DAB=90°.
(Ⅰ)如图1,连接BD,若⊙O的半径为6,,求AB的长;
(Ⅱ)如图2,连接AC,若AD=5,AB=3,对角线AC平分∠DAB,求AC的长.
23.如图,四边形ABDC内接于⊙O,∠BAC=60°,AD平分∠BAC交⊙O于点D,连接OB、OC、BD、CD.
(1)求证:四边形OBDC是菱形;
(2)若∠ABO=15°,OB=1,求弦AC长.
答案
一.选择题
B.D.A.A.C.B.C.D.C.D.
二.填空题
11.110°.
12.100°.
13.50.
14.50°.
15.2.
16.65.
三.解答题
17.解:(1)∵四边形ABCD为⊙O的内接四边形,
∴∠C+∠A=180°,
∵∠C=2∠A,
∴∠A=60°;
(2)连接OB,OD,作OH⊥BD于H
∵∠A=60°,∠BOD=2∠A,
∴∠BOD=120°;
又∵OB=OD,
∴∠OBD=∠ODB=30°,
∵OH⊥BD于H,
在Rt△DCP中,,
∴,
∵OH⊥BD于H,
∴.
18.(1)证明:∵四边形ABCD内接于圆,
∴∠CDE=∠ABC,
由圆周角定理得,∠ACB=∠ADB,又∠ADB=∠FDE,
∴∠ACB=∠FDE,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠FDE=∠CDE,即DE平分∠CDF;
(2)∵∠ACB=∠ABC,
∴∠CAE+∠E=∠ABD+∠DBC,
又∠CAE=∠DBC,
∴∠E=∠ABD,
∴∠ACD=∠AEB.
19.(1)解:∵CB=CD,
∴∠CDB=∠CBD=40°,
由圆周角定理得,∠CAB=∠CDB=40°,∠CAD=∠CBD=40°,
∴∠BAD=40°+40°=80°;
(2)证明:∵CE=CB,
∴∠CBE=∠CEB,
∴∠1+∠CDB=∠2+∠CAB,
∵∠BAC=∠BDC=∠CBD,
∴∠1=∠2.
20.解:(1)∵BC=CD,
∴=,
∴∠CAD=∠CAB=∠BAD=35°;
(2)连接BD,
∵AB=BC,
∴∠BAC=∠BCA,
∵OC∥AB,
∴∠BAC=∠OCA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠BAC=∠BCA=∠OAC,
由圆周角定理得,∠BCA=∠BDA,
∴∠BAC=∠BDA=∠OAC,
∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠ACO=30°.
21.解:(1)∵AB=AC,
∠B=∠C,
∵四边形AFDC是圆内接四边形,
∴∠AFD+∠C=∠BFD+∠AFD=180°,
∴∠BFD=∠C,
∴∠BFD=∠B,
∴BD=DF,
∴△BDF是等腰三角形;
(2)如图,已知AB=DE,∠B=∠E,
则四边形ABDE是平行四边形是假命题;
∵=,
∴DE=AC,
∵AB=AC,
∴AB=DE,
∵AB=AC,
∴∠B=∠C,
∵∠C=∠E,
∴∠B=∠E,
﹣=﹣,
∴=,
∴AE=CD>BD,
但四边形ABDE不是平行四边形,
∴“一组对边相等,且一组对角相等的四边形是平行四边形”是假命题.
22.解:(Ⅰ)如图1,
∵∠DAB=90°,
∴BD为直径,即BD=12,
∵,
∴AD=AB,
∴△ABD为等腰直角三角形,
∴AB=BD=6;
(Ⅱ)如图2,作BH⊥AC于H,
∵∠DAB=90°,
∴BD为直径,BD==,
∴∠BCD=90°,
∵AC平分∠DAB,
∴∠BAC=∠BAC=45°,
∴∠CBD=∠BDC=45°,
∴△CDB为等腰直角三角形,
∴BC=BD=×=,
在Rt△ABH中,AH=BH=AB=,
在Rt△BCH中,CH==,
∴AC=AH+CH=+=4.
23.(1)证明:连接OD,
由圆周角定理得,∠BOC=2∠BAC=120°,
∵AD平分∠BAC,
∴=,
∴∠BOD=∠COD=60°,
∵OB=OD,OC=OD,
∴△BOD和△COD是等边三角形,
∴OB=BD=DC=OC,
∴四边形OBDC是菱形;
(2)解:连接OA,
∵OB=OA,∠ABO=15°,
∴∠AOB=150°,
∴∠AOC=360°﹣150°﹣120°=90°,
∴AC==.
一.选择题
1.如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )
A.70° B.110° C.130° D.140°
2.如图,四边形ABCD内接于⊙O,∠BOD=110°,那么∠BCD等于( )
A.110° B.135° C.55° D.125°
3.如图,点A、B、C、D在⊙O上,四边形OBCD是平行四边形,则∠A的大小为( )
A.30° B.45° C.60° D.无法确定
4.如图,四边形ABCD是半圆的内接四边形,AB是直径,点C是的中点,如果∠DAB=70°,则∠ABC的度数等于( )
A.55° B.60° C.65° D.70°
5.如图,四边形ABCD内接于圆,并有:::=4:5:6:5,则∠B的度数为( )
A.90° B.95° C.99° D.100°
6.如图,五边形ABCDE内接于⊙O,若∠CAD=35°,则∠B+∠E的度数是( )
A.210° B.215° C.235° D.250°
7.已知圆内接四边形ABCD中,∠A:∠B:∠C=1:2:3,则∠D的大小是( )
A.45° B.60° C.90° D.135°
8.如图,四边形ABCD内接于⊙O,AB是直径,BC∥OD,若∠C=130°,则∠B的度数为( )
A.50° B.60° C.70° D.80°
9.下列说法正确的有( )
①平分弦的直径垂直于弦.②半圆所对的圆周角是直角.③一条弧所对的圆周角等于它所对的圆心角的一半.④在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等.⑤圆内接平行四边形是矩形.
A.1个 B.2个 C.3个 D.4个
10.如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE=,则AE=( )
A.3 B.3 C.4 D.2
二.填空题
11.如图,已知AB是半圆O的直径,∠BAC=20°,D是弧AC上任意一点,则∠D的度数是 .
12.如图,四边形ABCD内接于⊙O,AC平分∠BAD.若∠BDC=40°,则∠BCD的度数为 .
13.如图,四边形ABCD内接于⊙O,延长CO交圆于点E,连接.若∠A=110°,∠E=70°,则∠OCD= 度.
14.如图,四边形ABCD内接于圆,点B关于对角线AC的对称点E落在边CD上,连接AE.若∠ABC=115°,则∠DAE的度数为 .
15.如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长 .
16.如图所示,四边形ABCD内接于⊙O,AB=AD,∠BCE=50°,连接BD,则∠ABD= 度.
三.解答题
17.已知如图,⊙O的半径为4,四边形ABCD为⊙O的内接四边形,且∠C=2∠A.
(1)求∠A的度数.
(2)求BD的长.
18.如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,AB=AC.
(1)求证:DE平分∠CDF;
(2)求证:∠ACD=∠AEB.
19.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=40°,求∠BAD的度数;
(2)求证:∠1=∠2.
20.四边形ABCD内接于⊙O,AC为其中一条对角线.
(Ⅰ)如图①,若∠BAD=70°,BC=CD.求∠CAD的大小;
(Ⅱ)如图②,若AD经过圆心O,连接OC,AB=BC,OC∥AB,求∠ACO的大小.
21.已知,如图△ABC中,AB=AC,D是边BC上一点,BD<DC,过点A、D、C三点的⊙O交AB于点F,点E在上,连接DF、AE、DE、CE.
(1)求证:△BDF是等腰三角形;
(2)若,请用题意可以推出的结论说明命题:“一组对边相等,且一组对角相等的四边形是平行四边形”是假命题.
22.已知四边形ABCD内接于⊙O,∠DAB=90°.
(Ⅰ)如图1,连接BD,若⊙O的半径为6,,求AB的长;
(Ⅱ)如图2,连接AC,若AD=5,AB=3,对角线AC平分∠DAB,求AC的长.
23.如图,四边形ABDC内接于⊙O,∠BAC=60°,AD平分∠BAC交⊙O于点D,连接OB、OC、BD、CD.
(1)求证:四边形OBDC是菱形;
(2)若∠ABO=15°,OB=1,求弦AC长.
答案
一.选择题
B.D.A.A.C.B.C.D.C.D.
二.填空题
11.110°.
12.100°.
13.50.
14.50°.
15.2.
16.65.
三.解答题
17.解:(1)∵四边形ABCD为⊙O的内接四边形,
∴∠C+∠A=180°,
∵∠C=2∠A,
∴∠A=60°;
(2)连接OB,OD,作OH⊥BD于H
∵∠A=60°,∠BOD=2∠A,
∴∠BOD=120°;
又∵OB=OD,
∴∠OBD=∠ODB=30°,
∵OH⊥BD于H,
在Rt△DCP中,,
∴,
∵OH⊥BD于H,
∴.
18.(1)证明:∵四边形ABCD内接于圆,
∴∠CDE=∠ABC,
由圆周角定理得,∠ACB=∠ADB,又∠ADB=∠FDE,
∴∠ACB=∠FDE,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠FDE=∠CDE,即DE平分∠CDF;
(2)∵∠ACB=∠ABC,
∴∠CAE+∠E=∠ABD+∠DBC,
又∠CAE=∠DBC,
∴∠E=∠ABD,
∴∠ACD=∠AEB.
19.(1)解:∵CB=CD,
∴∠CDB=∠CBD=40°,
由圆周角定理得,∠CAB=∠CDB=40°,∠CAD=∠CBD=40°,
∴∠BAD=40°+40°=80°;
(2)证明:∵CE=CB,
∴∠CBE=∠CEB,
∴∠1+∠CDB=∠2+∠CAB,
∵∠BAC=∠BDC=∠CBD,
∴∠1=∠2.
20.解:(1)∵BC=CD,
∴=,
∴∠CAD=∠CAB=∠BAD=35°;
(2)连接BD,
∵AB=BC,
∴∠BAC=∠BCA,
∵OC∥AB,
∴∠BAC=∠OCA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠BAC=∠BCA=∠OAC,
由圆周角定理得,∠BCA=∠BDA,
∴∠BAC=∠BDA=∠OAC,
∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠ACO=30°.
21.解:(1)∵AB=AC,
∠B=∠C,
∵四边形AFDC是圆内接四边形,
∴∠AFD+∠C=∠BFD+∠AFD=180°,
∴∠BFD=∠C,
∴∠BFD=∠B,
∴BD=DF,
∴△BDF是等腰三角形;
(2)如图,已知AB=DE,∠B=∠E,
则四边形ABDE是平行四边形是假命题;
∵=,
∴DE=AC,
∵AB=AC,
∴AB=DE,
∵AB=AC,
∴∠B=∠C,
∵∠C=∠E,
∴∠B=∠E,
﹣=﹣,
∴=,
∴AE=CD>BD,
但四边形ABDE不是平行四边形,
∴“一组对边相等,且一组对角相等的四边形是平行四边形”是假命题.
22.解:(Ⅰ)如图1,
∵∠DAB=90°,
∴BD为直径,即BD=12,
∵,
∴AD=AB,
∴△ABD为等腰直角三角形,
∴AB=BD=6;
(Ⅱ)如图2,作BH⊥AC于H,
∵∠DAB=90°,
∴BD为直径,BD==,
∴∠BCD=90°,
∵AC平分∠DAB,
∴∠BAC=∠BAC=45°,
∴∠CBD=∠BDC=45°,
∴△CDB为等腰直角三角形,
∴BC=BD=×=,
在Rt△ABH中,AH=BH=AB=,
在Rt△BCH中,CH==,
∴AC=AH+CH=+=4.
23.(1)证明:连接OD,
由圆周角定理得,∠BOC=2∠BAC=120°,
∵AD平分∠BAC,
∴=,
∴∠BOD=∠COD=60°,
∵OB=OD,OC=OD,
∴△BOD和△COD是等边三角形,
∴OB=BD=DC=OC,
∴四边形OBDC是菱形;
(2)解:连接OA,
∵OB=OA,∠ABO=15°,
∴∠AOB=150°,
∴∠AOC=360°﹣150°﹣120°=90°,
∴AC==.
同课章节目录
