九年级数学上册试题 4.4 两个三角形相似的判定-浙教版(含答案)
文档属性
| 名称 | 九年级数学上册试题 4.4 两个三角形相似的判定-浙教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 175.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 10:48:03 | ||
图片预览




文档简介
4.4 两个三角形相似的判定
一.选择题
1.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中能判断△ABC∽△AED的是( )
①∠AED=∠B;②∠ADE=∠C;③=;④=.
A.①② B.①②③ C.①②④ D.①②③④
2.如图,在△ABC中,若DE∥BC,,DE=4cm,则BC的长是( )
A.7cm B.10cm C.13cm D.15cm
3.如图,△ABC中,D、E两点分别在BC、AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F.则图中相似三角形的对数是( )
A.1 B.2 C.3 D.4
4.如图,在△ABC中,E,G分别是AB,AC上的点,∠AEG=∠C,∠BAC的平分线AD交EG于点F,交BC于点D,若,则下列结论正确的是( )
A. B. C. D.
5.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )
A.∠ACD=∠B B.CD2=AD BD
C.AC BC=AB CD D.BC2=AD AB
6.如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )
A.②④ B.②⑤ C.③④ D.④⑤
7.如图,AD∥BC,∠D=90°,AD=3,BC=4,DC=6,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有( )
A.1 个 B.2 个 C.3 个 D.4 个
8.如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与点A、C重合),DE与AB相交于点F,那么与△BFD相似的三角形是( )
A.△BFE B.△BDC C.△BDA D.△AFD
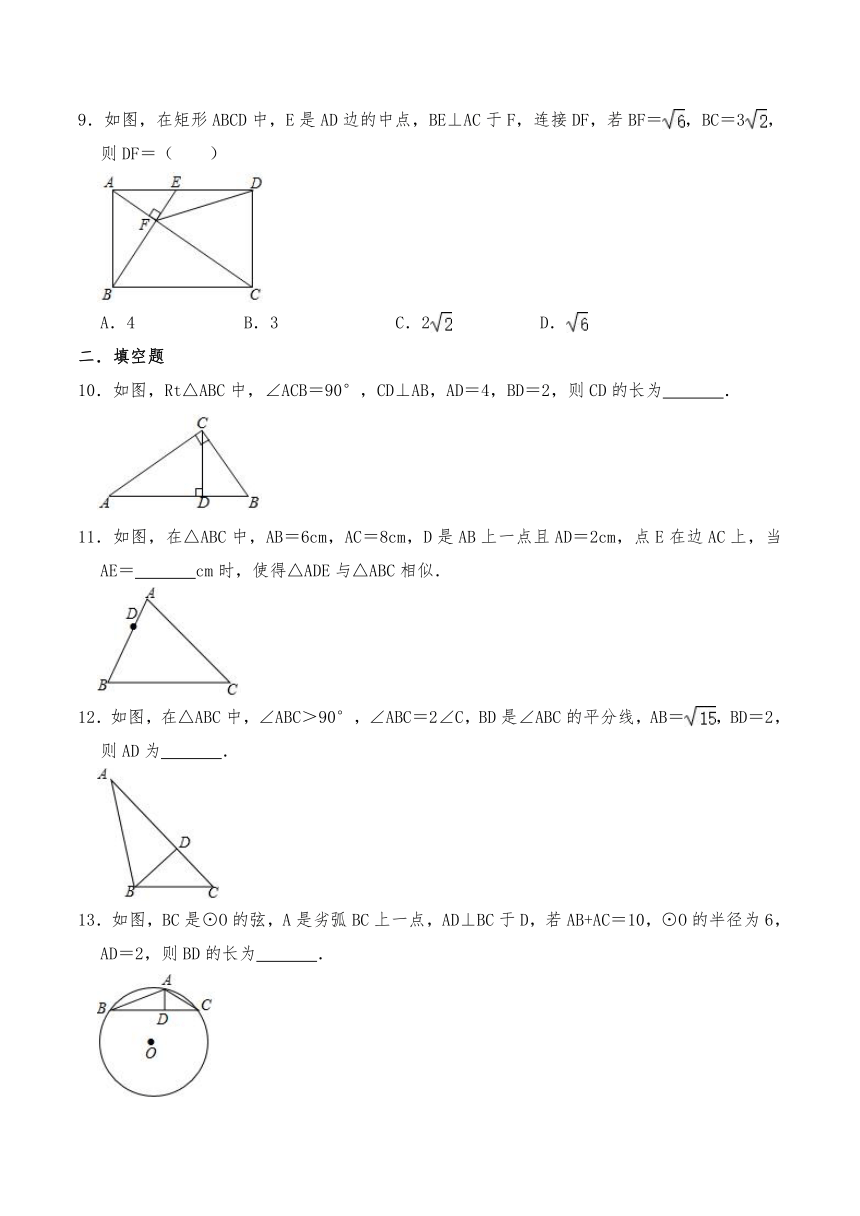
9.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于F,连接DF,若BF=,BC=3,则DF=( )
A.4 B.3 C.2 D.
二.填空题
10.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AD=4,BD=2,则CD的长为 .
11.如图,在△ABC中,AB=6cm,AC=8cm,D是AB上一点且AD=2cm,点E在边AC上,当AE= cm时,使得△ADE与△ABC相似.
12.如图,在△ABC中,∠ABC>90°,∠ABC=2∠C,BD是∠ABC的平分线,AB=,BD=2,则AD为 .
13.如图,BC是⊙O的弦,A是劣弧BC上一点,AD⊥BC于D,若AB+AC=10,⊙O的半径为6,AD=2,则BD的长为 .
14.在每个小正方形的边长都为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知△ABC是4×6的网格图形中的格点三角形,则该图中所有与△ABC相似的格点三角形中,最大的三角形面积是 .
15.如图,在四边形ABCD中,以AB为直径的半圆O经过点C,D.AC与BD相交于点E,CD2=CE CA,分别延长AB,DC相交于点P,PB=BO,CD=2.则BO的长是 .
16.如图,在矩形ABCD中,E为AB的中点,点F在BC上,且BF=2FC,AF与DE,DB分别相交于点G,H,则的值为 .
三.解答题
17.如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P,=.
(1)求证:∠APD=∠C;
(2)如果AB=3,DC=2,求AP的长.
18.如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,试说明:
(1)△ABE∽△ACD;
(2)AD BC=DE AC.
19.如图,AB为⊙O的直径,点C、D在⊙O上,AC=3,BC=4,且AC=AD,弦CD交直径AB于点E.
(1)求证:△ACE∽△ABC;
(2)求弦CD的长.
20.如图,已知点D为△ABC内一点,点E为△ABC外一点,且满足.
(1)求证:△ABD∽△ACE;
(2)联结CD,如果∠ADB=90°,∠BAD=∠ACD=30°,BC=,AC=4,求CD的长.
21.如图1,△ABC内接于⊙O,点D是的中点,且与点C位于AB的异侧,CD交AB于点E.
(1)求证:△ADE∽△CDA.
(2)如图2,若⊙O的直径AB=4,CE=2,求AD和CD的长.
22.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
23.如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE,且∠B=∠ADE=∠C.
(1)证明:△BDA∽△CED;
(2)若∠B=45°,BC=2,当点D在BC上运动时(点D不与B、C重合),且△ADE是等腰三角形,求此时BD的长.
答案
一、填空题
B.B.C.B.D.A.A.C.B.
二.填空题
10.2.
11.或1.5.
12.3.
13.2或4.
14.4.
15.4.
16..
三.解答题
17.证明:(1)∵PA⊥AB,DP⊥BC,
∴∠BAP=∠DPC=90°,
∵=
∴,
∴Rt△ABP∽Rt△PCD,
∴∠B=∠C,∠APB=∠CDP,
∵∠DPB=∠C+∠CDP=∠APB+∠APD,
∴∠APD=∠C;
(2)∵∠B=∠C,
∴AB=AC=3,且CD=2,
∴AD=1,
∵∠APD=∠C,∠CAP=∠PAD,
∴△APC∽△ADP,
∴
∴AP2=1×3=3
∴AP=.
18.解:(1)∵CD⊥AB于D,BE⊥AC于E,
∴∠AEB=∠ADC=90°,
在△ABE和△ACD中,
,
∴△ABE∽△ACD;
(2)∵△ABE∽△ACD,
∴,
在△ADE和△ACB中,
,
∴△ADE∽△ACB,
∴,
∴AD BC=DE AC.
19.解:(1)∵AC=AD,AB是⊙O的直径,
∴CD⊥AB,
∴∠AEC=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACE+∠BAC=∠BAC+∠B=90°,
∴∠ACE=∠B,
∴△ACE∽△ABC.
(2)由(1)可知:,
∴AC2=AE AB,
∵AC=3,BC=4,
∴由勾股定理可知:AB=5,
∴AE=,
∴由勾股定理可知:CE=,
∴由垂径定理可知:CD=2CE=.
20.证明:(1)∵,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE,
又∵,
∴△ABD∽△ACE;
(2)如图,
∵△ABD∽△ACE,
∴∠ADB=∠AEC=90°,∠BAD=∠CAE=30°,
∴CE=AC=2,AE=CE=2,∠ACE=60°,
∴∠DCE=∠ACD+∠ACE=90°,
∵,
∴=,
∴DE=3,
∴CD===.
21.解:(1)∵点D是的中点,
∴
∴∠ACD=∠BAD,
∵∠ADE=∠CDA
∴△ADE∽△CDA
(2)连结BD,
∵点D是的中点,
∴AD=BD
∵AB是⊙O的直径,
∴∠ADB=90°,
∴△ADB为等腰直角三角形,
∴,
由(1)得△ADE∽△CDA,
∴,即AD2=CD ED,
∴,
∴CD2﹣2CD﹣48=0,解得CD=8或﹣6.
∴CD=8.
22.解:根据勾股定理得:BA=;
(1)分两种情况讨论:
①当△BPQ∽△BAC时,,
∵BP=5t,QC=4t,AB=10,BC=8,
∴,解得,t=1,
②当△BPQ∽△BCA时,,
∴,解得,t=;
∴t=1或时,△BPQ∽△BCA;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,如图所示:
则PB=5t,PM=3t,MC=8﹣4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴,
∴,解得t=.
23.(1)证明:∵∠B=∠ADE=∠C,
∴∠BAD=180°﹣∠ADB﹣∠ADE,
∵∠CDE=180°﹣∠ADB﹣∠ADE,
∴∠BAD=∠CDE,
∴△BDA∽△CED;
(2)当AD=AE时,∴∠1=∠AED,
∵∠1=45°,
∴∠1=∠ADE=45°,
∴∠DAE=90°,
∴点D与B重合,不合题意舍去;
当EA=ED时,如图1,
∴∠EAD=∠1=45°,
∵∠BAC=90°,
∴∠BAD=∠EAD=45°,
∴AD平分∠BAC,
∴AD垂直平分BC,
∴BD=1;
当DA=DE时,如图2,
∵∠1=∠C,∠DAE=∠CAD,
∴△ADE∽△ACD,
∴DA:AC=DE:DC,
∴DC=CA=,
∴BD=BC﹣DC=2﹣,
∴综上所述,当△ADE是等腰三角形时,BD的长为1或2﹣.
一.选择题
1.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中能判断△ABC∽△AED的是( )
①∠AED=∠B;②∠ADE=∠C;③=;④=.
A.①② B.①②③ C.①②④ D.①②③④
2.如图,在△ABC中,若DE∥BC,,DE=4cm,则BC的长是( )
A.7cm B.10cm C.13cm D.15cm
3.如图,△ABC中,D、E两点分别在BC、AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F.则图中相似三角形的对数是( )
A.1 B.2 C.3 D.4
4.如图,在△ABC中,E,G分别是AB,AC上的点,∠AEG=∠C,∠BAC的平分线AD交EG于点F,交BC于点D,若,则下列结论正确的是( )
A. B. C. D.
5.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )
A.∠ACD=∠B B.CD2=AD BD
C.AC BC=AB CD D.BC2=AD AB
6.如图,在正方形网格上有5个三角形(三角形的顶点均在格点上):①△ABC,②△ADE,③△AEF,④△AFH,⑤△AHG,在②至⑤中,与①相似的三角形是( )
A.②④ B.②⑤ C.③④ D.④⑤
7.如图,AD∥BC,∠D=90°,AD=3,BC=4,DC=6,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有( )
A.1 个 B.2 个 C.3 个 D.4 个
8.如图,已知△ABC与△BDE都是等边三角形,点D在边AC上(不与点A、C重合),DE与AB相交于点F,那么与△BFD相似的三角形是( )
A.△BFE B.△BDC C.△BDA D.△AFD
9.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于F,连接DF,若BF=,BC=3,则DF=( )
A.4 B.3 C.2 D.
二.填空题
10.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AD=4,BD=2,则CD的长为 .
11.如图,在△ABC中,AB=6cm,AC=8cm,D是AB上一点且AD=2cm,点E在边AC上,当AE= cm时,使得△ADE与△ABC相似.
12.如图,在△ABC中,∠ABC>90°,∠ABC=2∠C,BD是∠ABC的平分线,AB=,BD=2,则AD为 .
13.如图,BC是⊙O的弦,A是劣弧BC上一点,AD⊥BC于D,若AB+AC=10,⊙O的半径为6,AD=2,则BD的长为 .
14.在每个小正方形的边长都为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知△ABC是4×6的网格图形中的格点三角形,则该图中所有与△ABC相似的格点三角形中,最大的三角形面积是 .
15.如图,在四边形ABCD中,以AB为直径的半圆O经过点C,D.AC与BD相交于点E,CD2=CE CA,分别延长AB,DC相交于点P,PB=BO,CD=2.则BO的长是 .
16.如图,在矩形ABCD中,E为AB的中点,点F在BC上,且BF=2FC,AF与DE,DB分别相交于点G,H,则的值为 .
三.解答题
17.如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P,=.
(1)求证:∠APD=∠C;
(2)如果AB=3,DC=2,求AP的长.
18.如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,试说明:
(1)△ABE∽△ACD;
(2)AD BC=DE AC.
19.如图,AB为⊙O的直径,点C、D在⊙O上,AC=3,BC=4,且AC=AD,弦CD交直径AB于点E.
(1)求证:△ACE∽△ABC;
(2)求弦CD的长.
20.如图,已知点D为△ABC内一点,点E为△ABC外一点,且满足.
(1)求证:△ABD∽△ACE;
(2)联结CD,如果∠ADB=90°,∠BAD=∠ACD=30°,BC=,AC=4,求CD的长.
21.如图1,△ABC内接于⊙O,点D是的中点,且与点C位于AB的异侧,CD交AB于点E.
(1)求证:△ADE∽△CDA.
(2)如图2,若⊙O的直径AB=4,CE=2,求AD和CD的长.
22.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
23.如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE,且∠B=∠ADE=∠C.
(1)证明:△BDA∽△CED;
(2)若∠B=45°,BC=2,当点D在BC上运动时(点D不与B、C重合),且△ADE是等腰三角形,求此时BD的长.
答案
一、填空题
B.B.C.B.D.A.A.C.B.
二.填空题
10.2.
11.或1.5.
12.3.
13.2或4.
14.4.
15.4.
16..
三.解答题
17.证明:(1)∵PA⊥AB,DP⊥BC,
∴∠BAP=∠DPC=90°,
∵=
∴,
∴Rt△ABP∽Rt△PCD,
∴∠B=∠C,∠APB=∠CDP,
∵∠DPB=∠C+∠CDP=∠APB+∠APD,
∴∠APD=∠C;
(2)∵∠B=∠C,
∴AB=AC=3,且CD=2,
∴AD=1,
∵∠APD=∠C,∠CAP=∠PAD,
∴△APC∽△ADP,
∴
∴AP2=1×3=3
∴AP=.
18.解:(1)∵CD⊥AB于D,BE⊥AC于E,
∴∠AEB=∠ADC=90°,
在△ABE和△ACD中,
,
∴△ABE∽△ACD;
(2)∵△ABE∽△ACD,
∴,
在△ADE和△ACB中,
,
∴△ADE∽△ACB,
∴,
∴AD BC=DE AC.
19.解:(1)∵AC=AD,AB是⊙O的直径,
∴CD⊥AB,
∴∠AEC=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACE+∠BAC=∠BAC+∠B=90°,
∴∠ACE=∠B,
∴△ACE∽△ABC.
(2)由(1)可知:,
∴AC2=AE AB,
∵AC=3,BC=4,
∴由勾股定理可知:AB=5,
∴AE=,
∴由勾股定理可知:CE=,
∴由垂径定理可知:CD=2CE=.
20.证明:(1)∵,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE,
又∵,
∴△ABD∽△ACE;
(2)如图,
∵△ABD∽△ACE,
∴∠ADB=∠AEC=90°,∠BAD=∠CAE=30°,
∴CE=AC=2,AE=CE=2,∠ACE=60°,
∴∠DCE=∠ACD+∠ACE=90°,
∵,
∴=,
∴DE=3,
∴CD===.
21.解:(1)∵点D是的中点,
∴
∴∠ACD=∠BAD,
∵∠ADE=∠CDA
∴△ADE∽△CDA
(2)连结BD,
∵点D是的中点,
∴AD=BD
∵AB是⊙O的直径,
∴∠ADB=90°,
∴△ADB为等腰直角三角形,
∴,
由(1)得△ADE∽△CDA,
∴,即AD2=CD ED,
∴,
∴CD2﹣2CD﹣48=0,解得CD=8或﹣6.
∴CD=8.
22.解:根据勾股定理得:BA=;
(1)分两种情况讨论:
①当△BPQ∽△BAC时,,
∵BP=5t,QC=4t,AB=10,BC=8,
∴,解得,t=1,
②当△BPQ∽△BCA时,,
∴,解得,t=;
∴t=1或时,△BPQ∽△BCA;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,如图所示:
则PB=5t,PM=3t,MC=8﹣4t,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴,
∴,解得t=.
23.(1)证明:∵∠B=∠ADE=∠C,
∴∠BAD=180°﹣∠ADB﹣∠ADE,
∵∠CDE=180°﹣∠ADB﹣∠ADE,
∴∠BAD=∠CDE,
∴△BDA∽△CED;
(2)当AD=AE时,∴∠1=∠AED,
∵∠1=45°,
∴∠1=∠ADE=45°,
∴∠DAE=90°,
∴点D与B重合,不合题意舍去;
当EA=ED时,如图1,
∴∠EAD=∠1=45°,
∵∠BAC=90°,
∴∠BAD=∠EAD=45°,
∴AD平分∠BAC,
∴AD垂直平分BC,
∴BD=1;
当DA=DE时,如图2,
∵∠1=∠C,∠DAE=∠CAD,
∴△ADE∽△ACD,
∴DA:AC=DE:DC,
∴DC=CA=,
∴BD=BC﹣DC=2﹣,
∴综上所述,当△ADE是等腰三角形时,BD的长为1或2﹣.
同课章节目录
