浙教版九年级数学上册4.5 相似三角形的性质及其应用试题(含答案)
文档属性
| 名称 | 浙教版九年级数学上册4.5 相似三角形的性质及其应用试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 149.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 00:00:00 | ||
图片预览


文档简介
4.5 相似三角形的性质及其应用
一.选择题
1.若△ABC∽△DEF,且S△ABC:S△DEF=5:4,则△ABC与△DEF的周长比为( )
A.5:4 B.4:5 C.2: D.:2
2.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,光源到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
A.21cm B.14cm C.6cm D.24cm
3.两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm B.60cm,100cm C.75cm,115cm D.85cm,125cm
4.如图,有一块形状为Rt△ABC的斜板余料.已知∠A=90°,AB=6cm,AC=8cm,要把它加工成一个形状为 DEFG的工件,使GF在BC上,D,E两点分别在AB,AC上,且DE=5cm,则 DEFG的面积为( )
A.24cm2 B.12cm2 C.9cm2 D.6cm2
5.如图,在等腰三角形△ABC中,AB=AC,图中所有三角形均相似,其中最小的三角形面积为1,△ABC的面积为44,则四边形DBCE的面积是( )
A.22 B.24 C.26 D.28
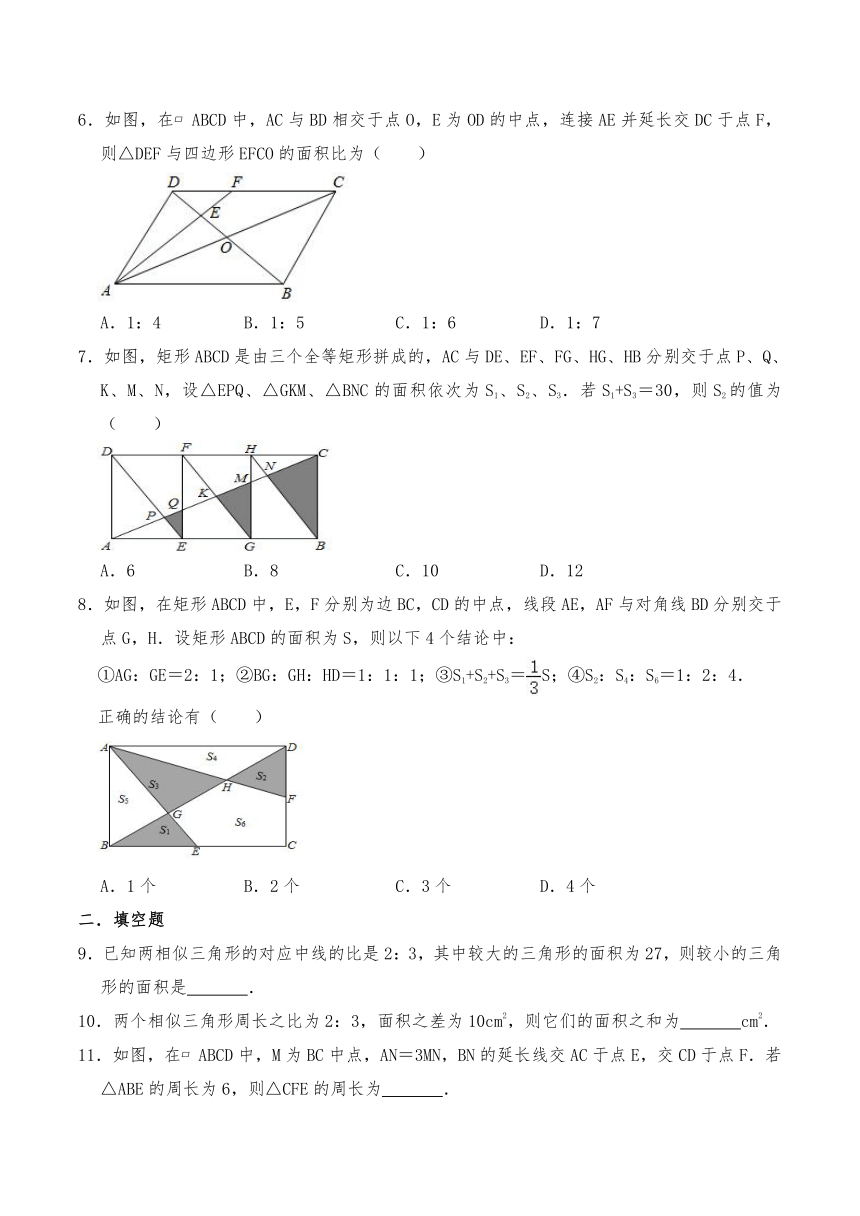
6.如图,在 ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则△DEF与四边形EFCO的面积比为( )
A.1:4 B.1:5 C.1:6 D.1:7
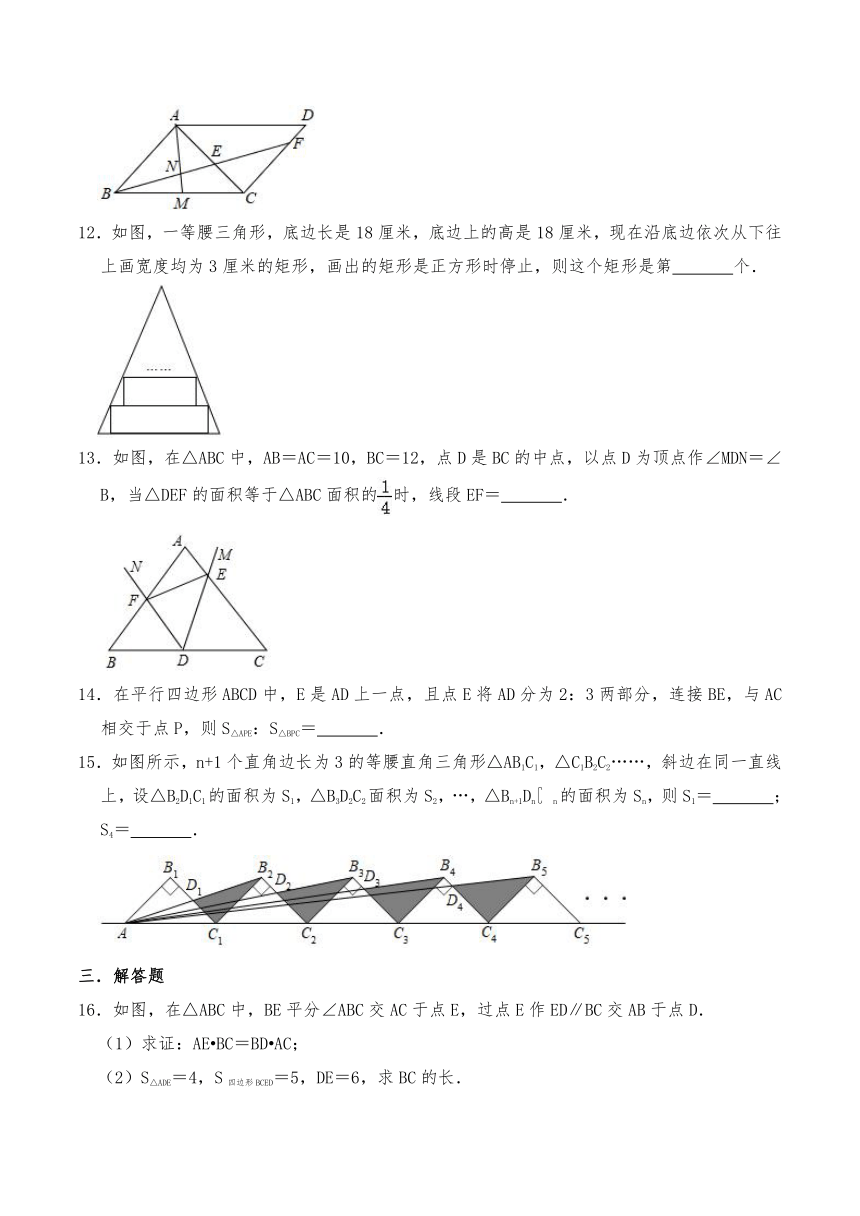
7.如图,矩形ABCD是由三个全等矩形拼成的,AC与DE、EF、FG、HG、HB分别交于点P、Q、K、M、N,设△EPQ、△GKM、△BNC的面积依次为S1、S2、S3.若S1+S3=30,则S2的值为( )
A.6 B.8 C.10 D.12
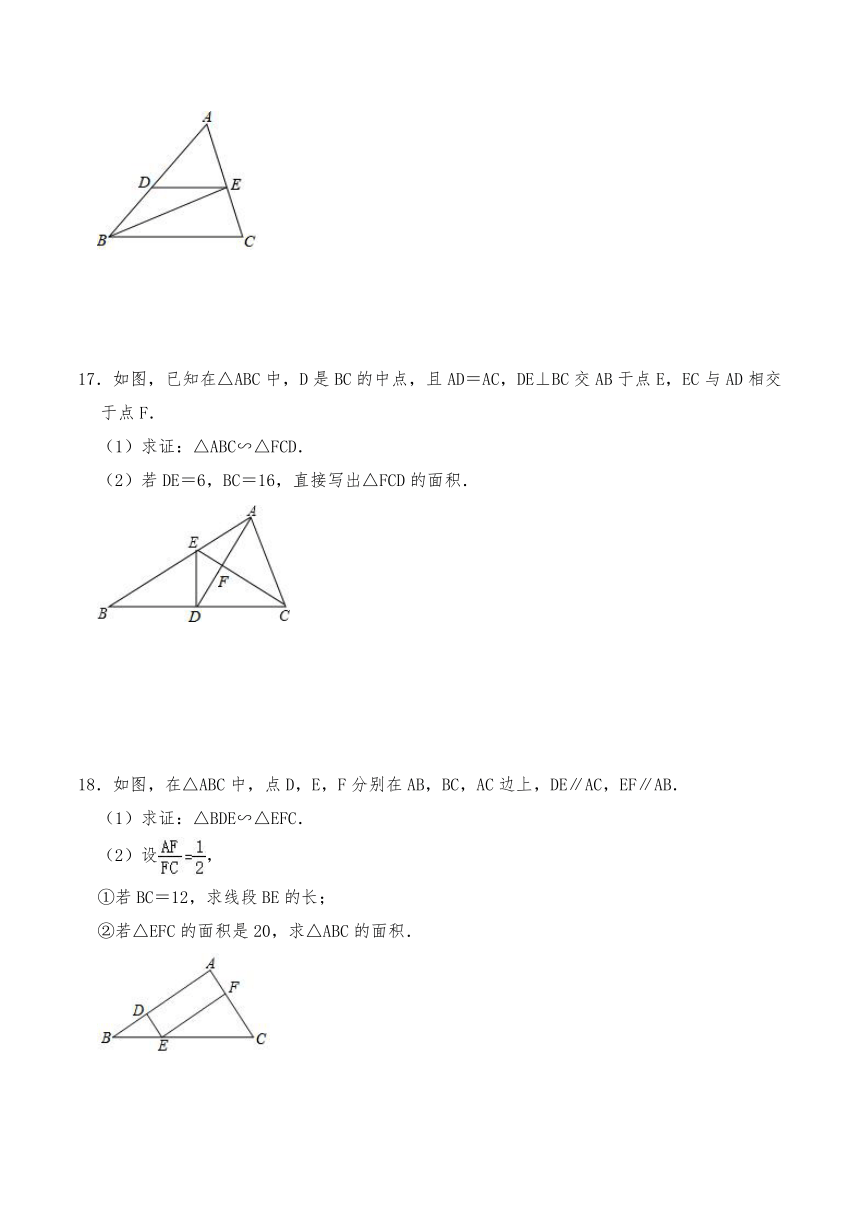
8.如图,在矩形ABCD中,E,F分别为边BC,CD的中点,线段AE,AF与对角线BD分别交于点G,H.设矩形ABCD的面积为S,则以下4个结论中:
①AG:GE=2:1;②BG:GH:HD=1:1:1;③S1+S2+S3=S;④S2:S4:S6=1:2:4.
正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
9.已知两相似三角形的对应中线的比是2:3,其中较大的三角形的面积为27,则较小的三角形的面积是 .
10.两个相似三角形周长之比为2:3,面积之差为10cm2,则它们的面积之和为 cm2.
11.如图,在 ABCD中,M为BC中点,AN=3MN,BN的延长线交AC于点E,交CD于点F.若△ABE的周长为6,则△CFE的周长为 .
12.如图,一等腰三角形,底边长是18厘米,底边上的高是18厘米,现在沿底边依次从下往上画宽度均为3厘米的矩形,画出的矩形是正方形时停止,则这个矩形是第 个.
13.如图,在△ABC中,AB=AC=10,BC=12,点D是BC的中点,以点D为顶点作∠MDN=∠B,当△DEF的面积等于△ABC面积的时,线段EF= .
14.在平行四边形ABCD中,E是AD上一点,且点E将AD分为2:3两部分,连接BE,与AC相交于点P,则S△APE:S△BPC= .
15.如图所示,n+1个直角边长为3的等腰直角三角形△AB1C1,△C1B2C2……,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2面积为S2,…,△Bn+1Dn n的面积为Sn,则S1= ;S4= .
三.解答题
16.如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AE BC=BD AC;
(2)S△ADE=4,S四边形BCED=5,DE=6,求BC的长.
17.如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD.
(2)若DE=6,BC=16,直接写出△FCD的面积.
18.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
19.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度DE=3.5m,点F到地面的高度CF=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上.
(1)求BC的长.
(2)求灯泡到地面的高度AG.
20.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=,AB=10,求AE的长;
(3)若△CDE的面积是△OBF面积的,求的值.
21.如图,在菱形ABCD中,点E在BC边上(不与点B、C重合),连接AE、BD交于点G.
(1)若AG=BG,AB=4,BD=6,求线段DG的长;
(2)设BC=kBE,△BGE的面积为S,△AGD和四边形CDGE的面积分别为S1和S2,把S1和S2分别用k、S的代数式表示;
(3)求的最大值.
答案
一.选择题
D.A.C.B.D.B.D.D.
二.填空题
9.12.
10.26.
11.4.
12.5
13.5.
14.或.
15.,.
三.解答题
16.(1)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵DE∥BC,
∴∠DBE=∠CBE,
∴∠ABE=∠DEB,
∴BD=DE,
∵DE∥BC,
∴△ADE∽△ABC,
∴,
∴,
∴AE BC=BD AC;
(2)解:∵S△ADE=4,S四边形BCED=5,
∴S△ABC=S△ADE+S四边形BCED=4+5=9,
∵△ADE∽△ABC,
∴,
∴,
∴BC=9.
17.证明:∵AD=AC,
∴∠ADC=∠ACD,
∵D是BC的中点,ED⊥BC,
∴BE=EC,
∴∠ABC=∠ECD,
∴△ABC∽△FCD;
(2)如图,过点A作AH⊥BC于H,
∵BC=16,D是BC的中点,
∴CD=BD=8,
∵AD=AC,AH⊥CD,
∴DH=CH=4,
∴BH=12,
∵DE∥AH,
∴,
∴,
∴AH=9,
∵△ABC∽△FCD
∴=()2,
∴S△FCD=×S△ABC=18.
18.(1)证明:∵DE∥AC,
∴∠DEB=∠FCE,
∵EF∥AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC;
(2)解:①∵EF∥AB,
∴==,
∵EC=BC﹣BE=12﹣BE,
∴=,
解得:BE=4;
②∵=,
∴=,
∵EF∥AB,
∴△EFC∽△BAC,
∴=()2=()2=,
∴S△ABC=S△EFC=×20=45.
19.解:(1)由题意可得:FC∥DE,
则△BFC∽BED,
故,
即,
解得:BC=3;
(2)∵AC=5.4m,
∴AB=5.4﹣3=2.4(m),
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA,
又∵∠FCB=∠GAB,
∴△BGA∽△BFC,
∴=,
∴,
解得:AG=1.2(m),
答:灯泡到地面的高度AG为1.2m.
20.解:(1)连接AD,
∵AB是⊙O直径,
∴∠AEB=∠ADB=90°,
∵AB=AC,
∴,
∴OD⊥BE;
(2)∵∠AEB=90°,
∴∠BEC=90°,
∵BD=CD,
∴BC=2DE=,
∵四边形ABDE内接于⊙O,
∴∠BAC+∠BDE=180°,
∵∠CDE+∠BDE=180°,
∴∠CDE=∠BAC,
∵∠C=∠C,
∴△CDE∽△CAB,
∴,即,
∴CE=2,
∴AE=AC﹣CE=AB﹣CE=8;
(3)∵,
∴设S△CDE=5k,S△OBF=6k,
∵BD=CD,
∴S△CDE=S△BDE=5k,
∵BD=CD,AO=BO,
∴OD∥AC,
∴△OBF∽△ABE,
∴,
∴S△ABE=4S△OBF,
∴S△ABE=4S△OBF=24k,
∴S△CAB=S△CDE+S△BDE+S△ABE=34k,
∵△CDE∽△CAB,
∴,
∴,
∵BC=2CD,
∴.
21.解:(1)∵AG=BG,
∴∠BAG=∠ABG,
∵四边形ABCD为菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠BAG=∠ADB,
∴△BAG∽△BDA,
∴=,即=,
∴BG=,
∴DG=BD﹣BG=6﹣=;
(2)∵四边形ABCD为菱形,
∴BC=AD=kBE,AD∥BC,
∵AD∥BE,
∴∠DAE=∠BEA,∠ADG=∠BEG
∴△ADG∽△EBG,
∴=()2=k2,==k,
∴S1=k2S,
∵==k,
∴S△ABG=,
∵△ABD的面积=△BDC的面积,
∴S2=S1+﹣S=k2S+kS﹣S=(k2+k﹣1)S;
(3)∵==1+﹣=﹣(﹣)2+,
∴的最大值为.
一.选择题
1.若△ABC∽△DEF,且S△ABC:S△DEF=5:4,则△ABC与△DEF的周长比为( )
A.5:4 B.4:5 C.2: D.:2
2.如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,光源到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
A.21cm B.14cm C.6cm D.24cm
3.两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm B.60cm,100cm C.75cm,115cm D.85cm,125cm
4.如图,有一块形状为Rt△ABC的斜板余料.已知∠A=90°,AB=6cm,AC=8cm,要把它加工成一个形状为 DEFG的工件,使GF在BC上,D,E两点分别在AB,AC上,且DE=5cm,则 DEFG的面积为( )
A.24cm2 B.12cm2 C.9cm2 D.6cm2
5.如图,在等腰三角形△ABC中,AB=AC,图中所有三角形均相似,其中最小的三角形面积为1,△ABC的面积为44,则四边形DBCE的面积是( )
A.22 B.24 C.26 D.28
6.如图,在 ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则△DEF与四边形EFCO的面积比为( )
A.1:4 B.1:5 C.1:6 D.1:7
7.如图,矩形ABCD是由三个全等矩形拼成的,AC与DE、EF、FG、HG、HB分别交于点P、Q、K、M、N,设△EPQ、△GKM、△BNC的面积依次为S1、S2、S3.若S1+S3=30,则S2的值为( )
A.6 B.8 C.10 D.12
8.如图,在矩形ABCD中,E,F分别为边BC,CD的中点,线段AE,AF与对角线BD分别交于点G,H.设矩形ABCD的面积为S,则以下4个结论中:
①AG:GE=2:1;②BG:GH:HD=1:1:1;③S1+S2+S3=S;④S2:S4:S6=1:2:4.
正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
9.已知两相似三角形的对应中线的比是2:3,其中较大的三角形的面积为27,则较小的三角形的面积是 .
10.两个相似三角形周长之比为2:3,面积之差为10cm2,则它们的面积之和为 cm2.
11.如图,在 ABCD中,M为BC中点,AN=3MN,BN的延长线交AC于点E,交CD于点F.若△ABE的周长为6,则△CFE的周长为 .
12.如图,一等腰三角形,底边长是18厘米,底边上的高是18厘米,现在沿底边依次从下往上画宽度均为3厘米的矩形,画出的矩形是正方形时停止,则这个矩形是第 个.
13.如图,在△ABC中,AB=AC=10,BC=12,点D是BC的中点,以点D为顶点作∠MDN=∠B,当△DEF的面积等于△ABC面积的时,线段EF= .
14.在平行四边形ABCD中,E是AD上一点,且点E将AD分为2:3两部分,连接BE,与AC相交于点P,则S△APE:S△BPC= .
15.如图所示,n+1个直角边长为3的等腰直角三角形△AB1C1,△C1B2C2……,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2面积为S2,…,△Bn+1Dn n的面积为Sn,则S1= ;S4= .
三.解答题
16.如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AE BC=BD AC;
(2)S△ADE=4,S四边形BCED=5,DE=6,求BC的长.
17.如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD.
(2)若DE=6,BC=16,直接写出△FCD的面积.
18.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
19.如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度DE=3.5m,点F到地面的高度CF=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上.
(1)求BC的长.
(2)求灯泡到地面的高度AG.
20.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=,AB=10,求AE的长;
(3)若△CDE的面积是△OBF面积的,求的值.
21.如图,在菱形ABCD中,点E在BC边上(不与点B、C重合),连接AE、BD交于点G.
(1)若AG=BG,AB=4,BD=6,求线段DG的长;
(2)设BC=kBE,△BGE的面积为S,△AGD和四边形CDGE的面积分别为S1和S2,把S1和S2分别用k、S的代数式表示;
(3)求的最大值.
答案
一.选择题
D.A.C.B.D.B.D.D.
二.填空题
9.12.
10.26.
11.4.
12.5
13.5.
14.或.
15.,.
三.解答题
16.(1)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵DE∥BC,
∴∠DBE=∠CBE,
∴∠ABE=∠DEB,
∴BD=DE,
∵DE∥BC,
∴△ADE∽△ABC,
∴,
∴,
∴AE BC=BD AC;
(2)解:∵S△ADE=4,S四边形BCED=5,
∴S△ABC=S△ADE+S四边形BCED=4+5=9,
∵△ADE∽△ABC,
∴,
∴,
∴BC=9.
17.证明:∵AD=AC,
∴∠ADC=∠ACD,
∵D是BC的中点,ED⊥BC,
∴BE=EC,
∴∠ABC=∠ECD,
∴△ABC∽△FCD;
(2)如图,过点A作AH⊥BC于H,
∵BC=16,D是BC的中点,
∴CD=BD=8,
∵AD=AC,AH⊥CD,
∴DH=CH=4,
∴BH=12,
∵DE∥AH,
∴,
∴,
∴AH=9,
∵△ABC∽△FCD
∴=()2,
∴S△FCD=×S△ABC=18.
18.(1)证明:∵DE∥AC,
∴∠DEB=∠FCE,
∵EF∥AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC;
(2)解:①∵EF∥AB,
∴==,
∵EC=BC﹣BE=12﹣BE,
∴=,
解得:BE=4;
②∵=,
∴=,
∵EF∥AB,
∴△EFC∽△BAC,
∴=()2=()2=,
∴S△ABC=S△EFC=×20=45.
19.解:(1)由题意可得:FC∥DE,
则△BFC∽BED,
故,
即,
解得:BC=3;
(2)∵AC=5.4m,
∴AB=5.4﹣3=2.4(m),
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA,
又∵∠FCB=∠GAB,
∴△BGA∽△BFC,
∴=,
∴,
解得:AG=1.2(m),
答:灯泡到地面的高度AG为1.2m.
20.解:(1)连接AD,
∵AB是⊙O直径,
∴∠AEB=∠ADB=90°,
∵AB=AC,
∴,
∴OD⊥BE;
(2)∵∠AEB=90°,
∴∠BEC=90°,
∵BD=CD,
∴BC=2DE=,
∵四边形ABDE内接于⊙O,
∴∠BAC+∠BDE=180°,
∵∠CDE+∠BDE=180°,
∴∠CDE=∠BAC,
∵∠C=∠C,
∴△CDE∽△CAB,
∴,即,
∴CE=2,
∴AE=AC﹣CE=AB﹣CE=8;
(3)∵,
∴设S△CDE=5k,S△OBF=6k,
∵BD=CD,
∴S△CDE=S△BDE=5k,
∵BD=CD,AO=BO,
∴OD∥AC,
∴△OBF∽△ABE,
∴,
∴S△ABE=4S△OBF,
∴S△ABE=4S△OBF=24k,
∴S△CAB=S△CDE+S△BDE+S△ABE=34k,
∵△CDE∽△CAB,
∴,
∴,
∵BC=2CD,
∴.
21.解:(1)∵AG=BG,
∴∠BAG=∠ABG,
∵四边形ABCD为菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠BAG=∠ADB,
∴△BAG∽△BDA,
∴=,即=,
∴BG=,
∴DG=BD﹣BG=6﹣=;
(2)∵四边形ABCD为菱形,
∴BC=AD=kBE,AD∥BC,
∵AD∥BE,
∴∠DAE=∠BEA,∠ADG=∠BEG
∴△ADG∽△EBG,
∴=()2=k2,==k,
∴S1=k2S,
∵==k,
∴S△ABG=,
∵△ABD的面积=△BDC的面积,
∴S2=S1+﹣S=k2S+kS﹣S=(k2+k﹣1)S;
(3)∵==1+﹣=﹣(﹣)2+,
∴的最大值为.
同课章节目录
