2.5 直角三角形复习(浙江省温州市平阳县)
文档属性
| 名称 | 2.5 直角三角形复习(浙江省温州市平阳县) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-28 00:00:00 | ||
图片预览



文档简介
课件15张PPT。△ABD有什么特点?你发现了什么?由此你得出什么结论?如图所示,把等边三角形ABC纸片对折,折痕为AD.折一折(复习)理一理(一)直角三角形的性质:1、角的关系:直角三角形两锐角互余2、边的关系:斜边上的中线等于斜边的一半;30°角所对的直角边等于斜边的一半。勾股定理(二)直角三角形的判定:1、角的方法:有一个角等于90°;两锐角互余。2、边的方法:两边的平方和等于第三边的平方。做一做1.在△ABC中,若∠A+∠B=∠C,则△ABC一定是( )
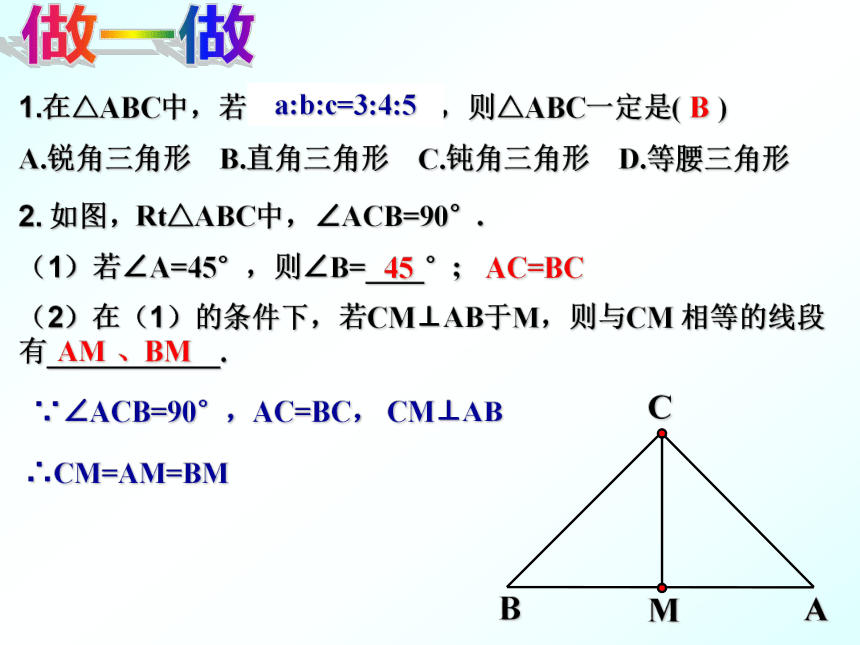
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形a=3,b=4,c=52. 如图,Rt△ABC中,∠ACB=90°.(1)若∠A=45°,则∠B=____°;(2)在(1)的条件下,若CM⊥AB于M,则与CM 相等的线段有____________.a:b:c=3:4:545AC=BCAM、BM∵∠ACB=90°,AC=BC, CM⊥AB∴CM=AM=BMB做一做1.在△ABC中,若∠A+∠B=∠C,则△ABC一定是( )
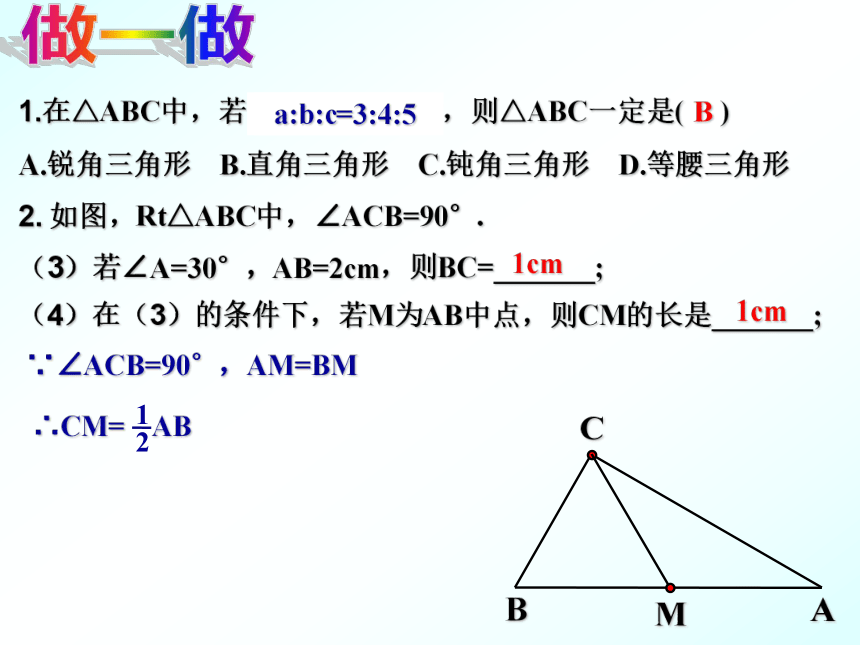
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形2. 如图,Rt△ABC中,∠ACB=90°.(3)若∠A=30°,AB=2cm,则BC=_______;(4)在(3)的条件下,若M为AB中点,则CM的长是_______;1cm1cmB∵∠ACB=90°,AM=BMa=3,b=4,c=5a:b:c=3:4:5做一做1.在△ABC中,若∠A+∠B=∠C,则△ABC一定是( )
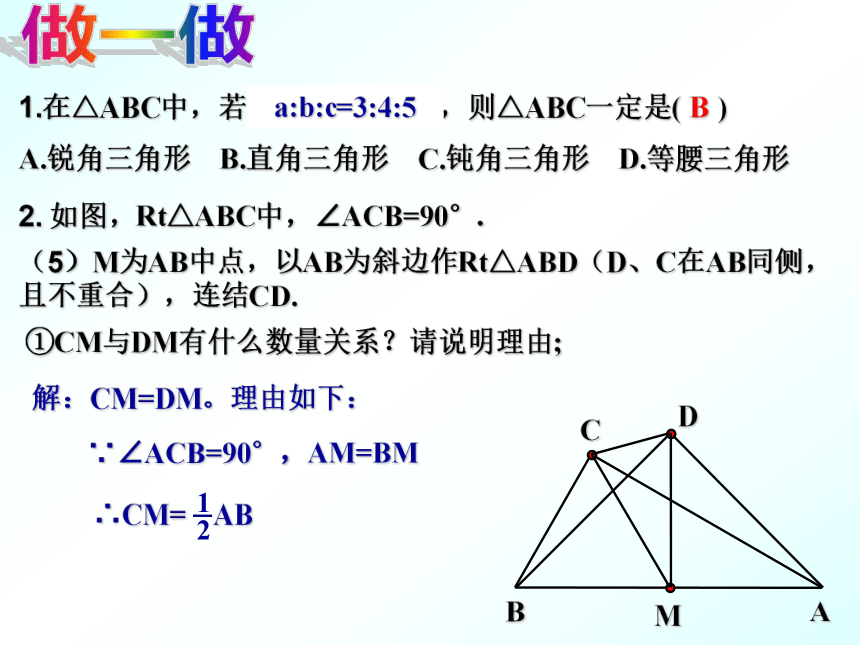
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形2. 如图,Rt△ABC中,∠ACB=90°.(5)M为AB中点,以AB为斜边作Rt△ABD(D、C在AB同侧,且不重合),连结CD.①CM与DM有什么数量关系?请说明理由;Ba=3,b=4,c=5a:b:c=3:4:5∵∠ACB=90°,AM=BM解:CM=DM。理由如下:做一做1.在△ABC中,若∠A+∠B=∠C,则△ABC一定是( )
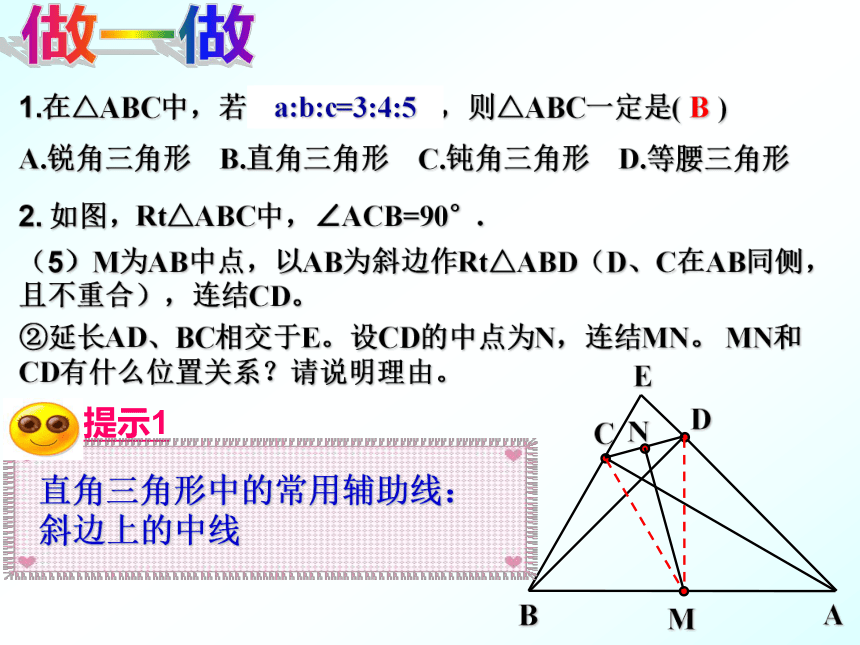
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形2. 如图,Rt△ABC中,∠ACB=90°.(5)M为AB中点,以AB为斜边作Rt△ABD(D、C在AB同侧,且不重合),连结CD。 ②延长AD、BC相交于E。设CD的中点为N,连结MN。 MN和CD有什么位置关系?请说明理由。直角三角形中的常用辅助线:
斜边上的中线Ba=3,b=4,c=5a:b:c=3:4:5做一做1.在△ABC中,若∠A+∠B=∠C,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形2. 如图,Rt△ABC中,∠ACB=90°.(5)以AB为斜边作Rt△ABD(D、C在AB同侧,且不重合)。③延长AD、BC相交于E,设AC、BD相交于H,若∠BAE=45°,则△BED≌________,请说明理由。Ba=3,b=4,c=5a:b:c=3:4:5△AHDAD=4cm, DE=1cm,则BH的长为_______.全等转化3cm练一练2. Rt△ABC中,两条边的长分别为3cm和4cm,则第三边的长为______________. 1. Rt△ABC中,两条直角边的长分别为3cm和4cm,则第三边的长为______;斜边上的高为______. 5cm2.4cm5cm面积方法分类思想3.如图,校园内有两棵树,相距12米,一颗树高13米,另一颗树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞______米. 13构造Rt△练一练直角三角形中线段计算的常用方法:
①面积方法;
②分类思想;
③构造Rt△;
④方程思想;
⑤全等转化.x510-x10-xD方程思想52+x2=(10-x)2议一议如图:已知∠C=∠D=90°,要使△ACB≌△BDA,还需要添加什么直接条件?如果添加条件为AC=BD,试说明OC=OD的理由。 三角板是我们常用的数学工具。下图是将一个三角板的直角顶点放在另一个等腰直角三角形斜边BC的中点D处转动,DE与AB交于点M,DF与AC交于点N(点M、N不与△ABC顶点重合),连结AD。试一试(1)图中与∠ADM一定相等的是哪一个角?为什么?(2)图中与△ADM一定全等的是哪一个三角形?为什么?本节课我的收获有……我感到困惑的是……1.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1位置时,说明△ADC≌△CEB的理由;(2)当直线MN绕点C旋转到图2位置时,说明DE=AD-BE的理由;(3)当直线MN绕点C旋转到图3位置时,试问DE、AD、BE有怎样的等量关系?请写出这个等量关系,并说明理由.图(1)图(2)2.如图,A、E、F、C在一条直线上,AE=CF,过E、F分别作DE ⊥AC,BF ⊥AC.(1)若AB=CD,说明BD平分EF;(2)若将△DEC的边EC沿AC方向移动变为图(2)时其余条件不变,上述结论是否成立,请说明理由。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形a=3,b=4,c=52. 如图,Rt△ABC中,∠ACB=90°.(1)若∠A=45°,则∠B=____°;(2)在(1)的条件下,若CM⊥AB于M,则与CM 相等的线段有____________.a:b:c=3:4:545AC=BCAM、BM∵∠ACB=90°,AC=BC, CM⊥AB∴CM=AM=BMB做一做1.在△ABC中,若∠A+∠B=∠C,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形2. 如图,Rt△ABC中,∠ACB=90°.(3)若∠A=30°,AB=2cm,则BC=_______;(4)在(3)的条件下,若M为AB中点,则CM的长是_______;1cm1cmB∵∠ACB=90°,AM=BMa=3,b=4,c=5a:b:c=3:4:5做一做1.在△ABC中,若∠A+∠B=∠C,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形2. 如图,Rt△ABC中,∠ACB=90°.(5)M为AB中点,以AB为斜边作Rt△ABD(D、C在AB同侧,且不重合),连结CD.①CM与DM有什么数量关系?请说明理由;Ba=3,b=4,c=5a:b:c=3:4:5∵∠ACB=90°,AM=BM解:CM=DM。理由如下:做一做1.在△ABC中,若∠A+∠B=∠C,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形2. 如图,Rt△ABC中,∠ACB=90°.(5)M为AB中点,以AB为斜边作Rt△ABD(D、C在AB同侧,且不重合),连结CD。 ②延长AD、BC相交于E。设CD的中点为N,连结MN。 MN和CD有什么位置关系?请说明理由。直角三角形中的常用辅助线:
斜边上的中线Ba=3,b=4,c=5a:b:c=3:4:5做一做1.在△ABC中,若∠A+∠B=∠C,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形2. 如图,Rt△ABC中,∠ACB=90°.(5)以AB为斜边作Rt△ABD(D、C在AB同侧,且不重合)。③延长AD、BC相交于E,设AC、BD相交于H,若∠BAE=45°,则△BED≌________,请说明理由。Ba=3,b=4,c=5a:b:c=3:4:5△AHDAD=4cm, DE=1cm,则BH的长为_______.全等转化3cm练一练2. Rt△ABC中,两条边的长分别为3cm和4cm,则第三边的长为______________. 1. Rt△ABC中,两条直角边的长分别为3cm和4cm,则第三边的长为______;斜边上的高为______. 5cm2.4cm5cm面积方法分类思想3.如图,校园内有两棵树,相距12米,一颗树高13米,另一颗树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞______米. 13构造Rt△练一练直角三角形中线段计算的常用方法:
①面积方法;
②分类思想;
③构造Rt△;
④方程思想;
⑤全等转化.x510-x10-xD方程思想52+x2=(10-x)2议一议如图:已知∠C=∠D=90°,要使△ACB≌△BDA,还需要添加什么直接条件?如果添加条件为AC=BD,试说明OC=OD的理由。 三角板是我们常用的数学工具。下图是将一个三角板的直角顶点放在另一个等腰直角三角形斜边BC的中点D处转动,DE与AB交于点M,DF与AC交于点N(点M、N不与△ABC顶点重合),连结AD。试一试(1)图中与∠ADM一定相等的是哪一个角?为什么?(2)图中与△ADM一定全等的是哪一个三角形?为什么?本节课我的收获有……我感到困惑的是……1.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1位置时,说明△ADC≌△CEB的理由;(2)当直线MN绕点C旋转到图2位置时,说明DE=AD-BE的理由;(3)当直线MN绕点C旋转到图3位置时,试问DE、AD、BE有怎样的等量关系?请写出这个等量关系,并说明理由.图(1)图(2)2.如图,A、E、F、C在一条直线上,AE=CF,过E、F分别作DE ⊥AC,BF ⊥AC.(1)若AB=CD,说明BD平分EF;(2)若将△DEC的边EC沿AC方向移动变为图(2)时其余条件不变,上述结论是否成立,请说明理由。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
