直角三角形复习课课件(浙江省温州市)

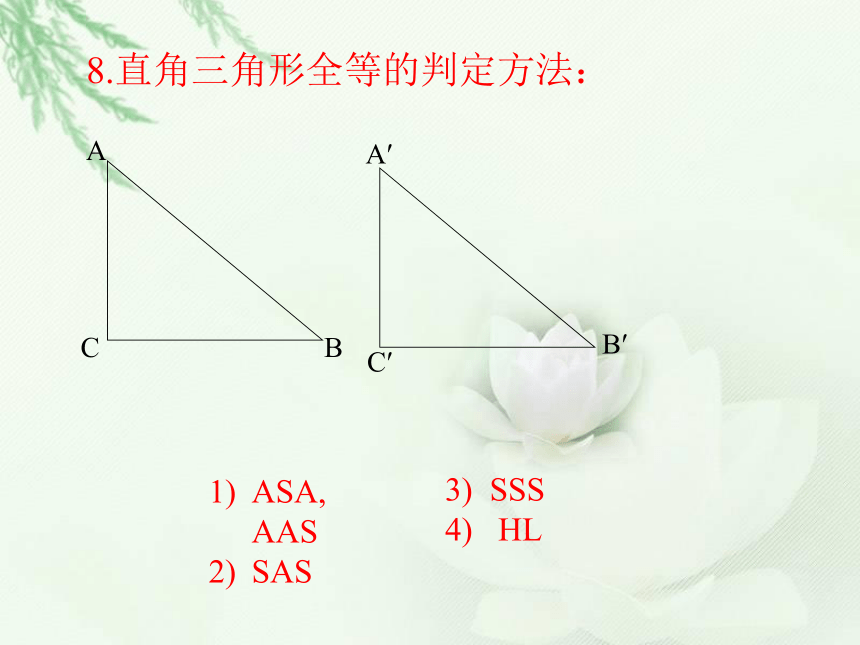
课件16张PPT。直角三角形复习课知识抢答
1 .在直角三角形中，两个锐角_____。
2两条直角边相等的直角三角形叫做_____ 等腰直角三角形的两个底角相等，都等于___ 度
3. 直角三角形_____________的平方和等于_______的平方。
如果用字母a,b和c分别表示直角三角形的两条直角边和斜边，那么_____+ _____=_____。
4.如果三角形中_______的平方和等于______边的平方，那么这个三角形是直角三角形，________所对的角是直角。
互余等腰直角三角形45两直角边斜边a2b2c2两边第三边最长边 5.直角三角形斜边上的中线等于 _____
6.在直角三角形中，如果一个锐角等于 _____度，那么它所对的直角边等于______的一半。
7.在角的内部，到角的两边距离相等的点在这个角的__________上。
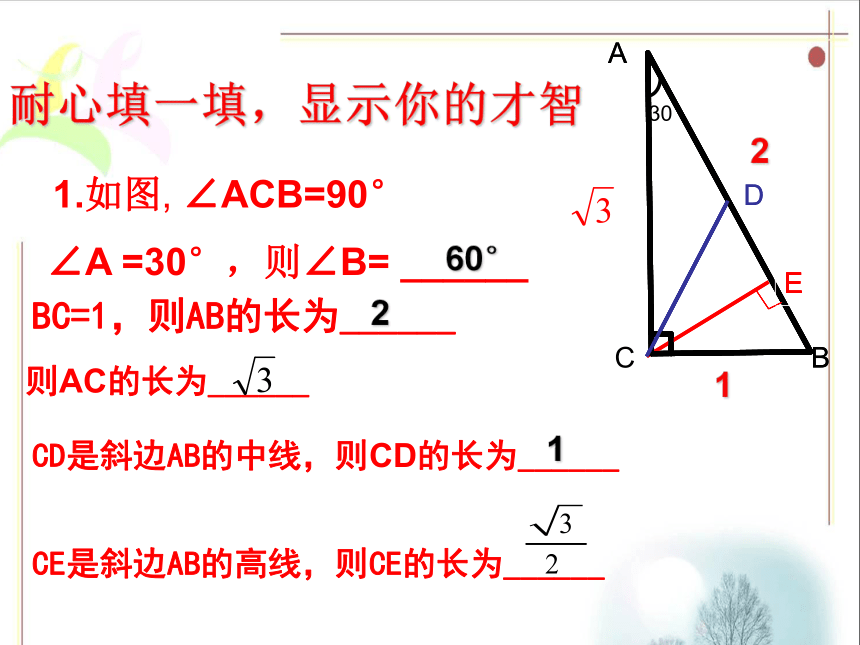
斜边的一半30斜边平分线C1.如图, ∠ACB=90° ∠A =30°，则∠B= ______BC=1，则AB的长为______CD是斜边AB的中线，则CD的长为______则AC的长为______CE是斜边AB的高线，则CE的长为______ 　　耐心填一填，显示你的才智60°21122.若直角三角形的两锐角之差为18°，则
较大一个锐角的度数是_______度。
3.直角三角形的两边长为3，4，则斜边上
的 中线长是 。542或5/2 例1. 如图，已知四边形ABCD中∠B=90°,AB=4,BC=3,AD=12,DC=13 ，
求四边形ABCD的面积解：连接AC
∵∠B=90°, AB=4, BC=3
∴由勾股定理得，AC=5
∵AD=12,DC=13
解答题，仔细做一做，千万别出错 .431312 1.如图已知四边形ABCD中， ∠A=60° ∠B=∠D=90°，BC=2，CD=1/2，求AB2。
练习解：延长AD，BC交于点E
∵∠A=60。 ∠B= ∠D=90 。
∴∠E=30
∴CD=1/2CE，AB=1/2AE，CD=1/2
∴CE=1，BE=3,
由勾股定理得: AB2+BE 2=AE2,
∴ AB2+32=(2AB)2, ∴ AB2= 3
21/2∟∟ 2.如图,直线l上有三个正方形A、B、C。若A、C的面积分别为5和11，则B的面积为多少？BAC解：作AD ⊥ BF
∵由已知可得：
∠ FBA=300
∴ AD= 1/2 AB=150KM
而 150＜200
所以A城会受到台风的影响思考：若A城与B地的方向保持不变，为了确保A城不受台风影响至少离B地多远？.例3：有一张Rt △ABC纸片如图所示：两直角边
AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠，
使它落在斜边AB上，且与AE重合，求CD的长。
ABCDE68合作学习
如图，在Rt△ABC中， ∠C=90°，AC=10cm，BC=5cm，一条线段PQ=AB，P，Q两点分别在AC上和过A点且垂直于AC的射线AM上运动，请探究当点P
满足什么条件时，△ABC和△PQA全等。QAPBCM解:当P点为AC中点或P点与C点重合时
△ABC和△PQA全等.
1)当P为AC中点时,PA=PC=5cm,
∴PA=CB,∵AB=QP
∴Rt △ABC≌ Rt △QPA(HL)
2)当P点与C点重合时,AC=PA
∵AB=PQ ∴Rt △ABC≌ Rt △PQA(HL)
ABCDE 如图，△ABC中，AB=AC，∠BAC=90°，D是BC上任意一点，则BD2+CD2=2AD2吗？请说明理由。
解 如图，将△ABD绕A点逆时针旋转90°至△ACE，连结DE，可得
∠DAE=∠DCE=90°，AE=AD，CE=BD
∴BD2+ CD2=CE2+CD2=DE2=2AD2.
挑战自我课堂作业
每位同学自编一道题目，能够运 用有关直角三角形的知识进行解答，
然后同桌之间交换解题。
再见 例1如图，AC与BD相交于点. O,DA⊥AC, DB⊥BC,AC=BD，说明OD=OC成立的理由.
ODCBA解：理由如下：连接DC，
∵ DA⊥AC DB⊥BC
∴∠A= ∠ B=RT∠
又∵AC=BD （已知） CD=DC（公共边）
∴Rt⊿ACD≌Rt⊿BDC（HL）
∴ ∠BDC= ∠ACD（全等三角形的对应角相等）
∴ OD=OC（等角对等边）